P中值选址问题的整数规划求解
P中值选址问题的整数规划求解
一 、P-中值问题
p-中值选址问题是一个常见的选址问题. 问题是给定I个需求结点和J个待选设施地点, 要求选择p个地点建立设施, 使得运输成本最低. 下面是个英文的问题详细描述:

二、整数规划模型
p-中值选址问题的整数规划模型如下
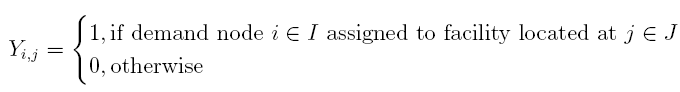

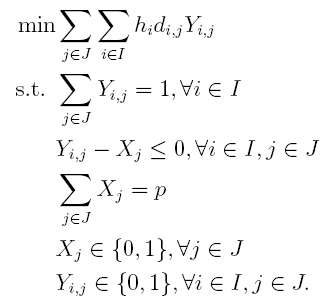
三、当给定距离时候的求解
假设给定了设施-需求之间的距离矩阵,照着上面的模型即可写出Leapms模型。
//==========================================================
//The P-Median Problem
//==========================================================
min sum{j=,...,J;i=,...,I}h[i]d[i][j]y[i][j]
subject to
sum{j=,...,J}y[i][j]=|i=,...,I
y[i][j]-x[j]<=|i=,...,I;j=,...,J
sum{j=,...,J}x[j]=p
where
I,J are numbers
p is a number
h is a set
d[i][j] is a number | i=,...,I;j=,...,J
x[j] is a variable of binary|j=,...,J
y[i][j] is a variable of binary|i=,...,I;j=,...,J data
I=
J=
p=
h={3.1,2.2,4.3,5.0,7.1,8.0,9.9,3.4,4.3,3.3}
d={ }
把上面的模型保存为pemedian1.leap
在leapms中求解: 依次输入load, pmedian1, mip即可求解
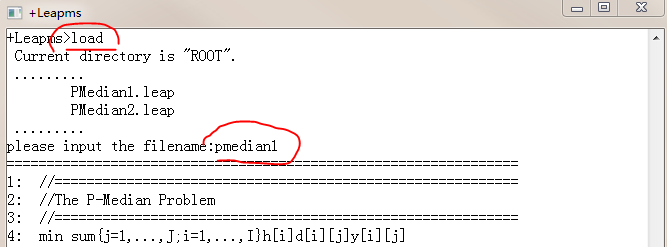
。。。 。。。

四、当给定设施和需求点坐标时候的求解
与上面类似,不过设施和需求点的距离需要用data_relation 段用公式表达出来,leapms表达的模型如下
//==========================================================
//The P-Median Problem
//==========================================================
min sum{j=1,...,J;i=1,...,I}h[i]d[i][j]y[i][j] subject to sum{j=1,...,J}y[i][j]=1|i=1,...,I
y[i][j]-x[j]<=0|i=1,...,I;j=1,...,J
sum{j=1,...,J}x[j]=p where
I,J are numbers
p is a number
h is a set cdx1[i],cdy1[i] are numbers|i=1,...,I
cdx2[j],cdy2[j] are numbers|j=1,...,J d[i][j] is a number | i=1,...,I;j=1,...,J
x[j] is a variable of binary|j=1,...,J
y[i][j] is a variable of binary|i=1,...,I;j=1,...,J data_relation d[i][j]=sqrt((cdx1[i]-cdx2[j])^2+(cdy1[i]-cdy2[j])^2)|-->
i=1,...,I;j=1,...,J
data
I=10
J=10 p=6
h={3.1, 2.2, 4.3, 5.0, 7.1, 8.0, 9.9, 3.4, 4.3, 3.3} cdx1={-9.7, 8.8,8.3,7.1,-6.8, 6.7,-5.8,0.7,7 , -6 }
cdy1={-8.3,-1.9,-0.1,-3, 4 , -4.1, 4.4,2.5,4.4, 8.8} cdx2={-1.9,-8.3,2.5,0.8,-2.2, 4.1,-1.2,9.2,-0.9,1}
cdy2={-6.6,-0.9,1 ,8.2, 0.5,-8.9,-2.2,9.5,-4 ,6}
把上面的模型保存为pemedian2.leap
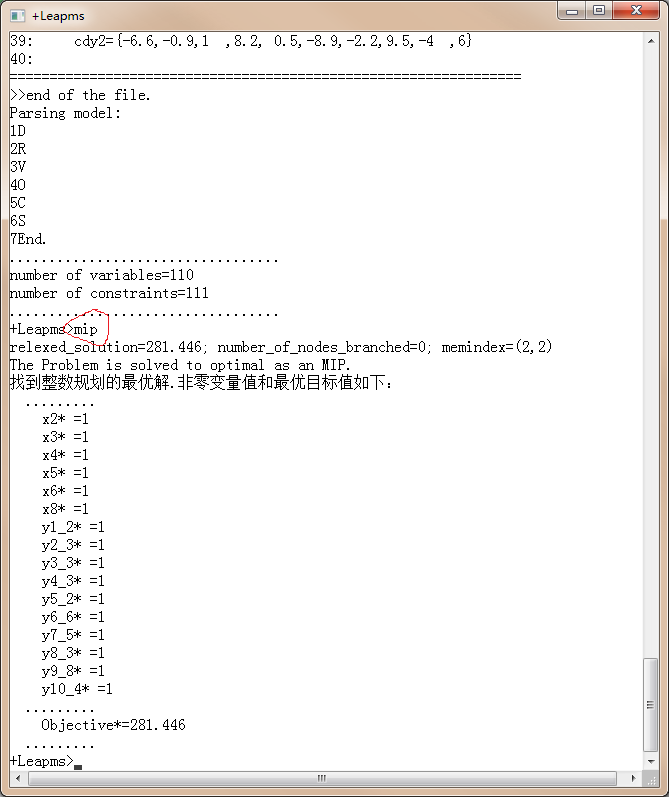
在leapms中求解: 依次输入load, pmedian2, mip即可求解
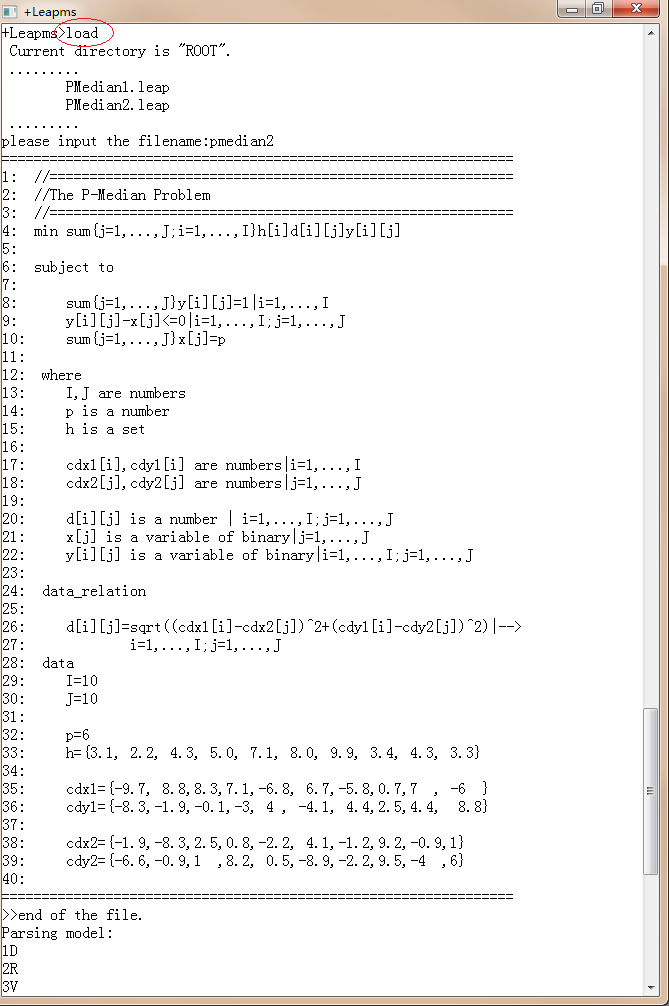
P中值选址问题的整数规划求解的更多相关文章
- OpenCV计算机视觉学习(4)——图像平滑处理(均值滤波,高斯滤波,中值滤波,双边滤波)
如果需要处理的原图及代码,请移步小编的GitHub地址 传送门:请点击我 如果点击有误:https://github.com/LeBron-Jian/ComputerVisionPractice &q ...
- 学习 opencv---(8)非线性滤波:中值滤波,双边滤波
正如我们上一篇文章中讲到的,线性滤波可以实现很多种不同的图像变换.然而非线性滤波,如中值滤波器和双边滤波器,有时可以达到更好的实现效果. 邻域算子的其他一些例子还有对 二值图像进行操作的形态学算子,用 ...
- js 实时监听input中值变化
注意:用到了jquery需要引入jquery.min.js. 需求: 1.每个地方需要分别打分,总分为100; 2.第一个打分总分为40; 3.第二个打分总分为60. 注意:需要判断null.&quo ...
- Atitit 图像处理 平滑 也称 模糊, 归一化块滤波、高斯滤波、中值滤波、双边滤波)
Atitit 图像处理 平滑 也称 模糊, 归一化块滤波.高斯滤波.中值滤波.双边滤波) 是一项简单且使用频率很高的图像处理方法 用途 去噪 去雾 各种线性滤波器对图像进行平滑处理,相关OpenC ...
- 平均值mean,众数mode,中值median 和 标准差stddev
平均值mean,众数mode,中值median 和 标准差stddev 均值,众数,中位数,标称差: 均值是就全部数据计算的,它具有优良的数学性质,是实际中应用最广泛的集中趋势测度值.其主要缺点是易受 ...
- OpenCv高斯,中值,均值,双边滤波
#include "cv.h" #include "highgui.h" #include <iostream> using namespace s ...
- opencv实现图像邻域均值滤波、中值滤波、高斯滤波
void CCVMFCView::OnBlurSmooth()//邻域均值滤波 { IplImage* in; in = workImg; IplImage* out = cvCreateImage( ...
- 中值排序的java实现
public class MidSort { public static void main(String[] args){ ,,,,,,,,}; midSort(arr,,); for(int i: ...
- java中值类型和引用类型的区别
[定义] 引用类型表示你操作的数据是同一个,也就是说当你传一个参数给另一个方法时,你在另一个方法中改变这个变量的值,那么调用这个方法是传入的变量的值也将改变. 值类型表示复制一个当前变量传给方法,当你 ...
随机推荐
- HikariCP重要参数配置
概述 HikariCP是Spring Framework 5.0的默认数据库连接池,这得益于他的高性能.但是如果配置不当,数据库连接池也可能因影响到系统性能. 重要参数 maximum-pool-si ...
- JavaScript ES6函数式编程(一):闭包与高阶函数
函数式编程的历史 函数的第一原则是要小,第二原则则是要更小 -- ROBERT C. MARTIN 解释一下上面那句话,就是我们常说的一个函数只做一件事,比如:将字符串首字母和尾字母都改成大写,我们此 ...
- Django实现WebSSH操作Kubernetes Pod
优秀的系统都是根据反馈逐渐完善出来的 上篇文章介绍了我们为了应对安全和多分支频繁测试的问题而开发了一套Alodi系统,Alodi可以通过一个按钮快速构建一套测试环境,生成一个临时访问地址,详细信息可以 ...
- 实验吧之【who are you?】(时间盲注)
地址:http://ctf5.shiyanbar.com/web/wonderkun/index.php 这道题点开看见your ip is :xxx.xxx.xx.xxx 试了一些 最后发现是XFF ...
- HMLT clear 属性
原文 : http://www.zhangxinxu.com/wordpress/2014/06/understand-css-clear-left-right-and-use/ clear 的四个值 ...
- 素数与Miller-Rabin测试
素数及其性质 素数又称质数.指整数在一个大于 111 的自然数中,除了 111 和此整数自身外,没法被其他自然数整除的数. 性质1 有无穷多个素数. 证明: 用反证法.设已知的最大素数为 PPP,考虑 ...
- 百万年薪python之路 -- 并发编程之 多进程二
1. 僵尸进程和孤儿进程 基于unix的环境(linux,macOS) 主进程需要等待子进程结束之后,主进程才结束 主进程时刻检测子进程的运行状态,当子进程结束之后,一段时间之内,将子进程进行回收. ...
- openresty性能测试报告分析
一.openresty介绍 1.什么是openresty 通过揉和众多设计良好的 Nginx 模块,OpenResty 有效地把 Nginx 服务器转变为一个强大的 Web 应用服务器,基于它开发人员 ...
- 巨杉Tech | SequoiaDB数据域及存储规划
1 背景近年来,企业的各项业务发展迅猛,客户数目不断增加,后台服务系统压力也越来越大,系统的各项硬件资源也变得非常紧张.因此,在技术风险可控的基础上,希望引入大数据技术,利用大数据技术优化现有IT系统 ...
- webpack 4.x 初级学习记录
首先声明下,本人不擅长文字表达,文采不行,所以文章中文字较少,请看代码,初级学习,不足之处请多多指教 GitHub链接 看云kancloud [TOC] webpack 4.x 安装 首先需要在全局中 ...
