局部敏感哈希LSH（Locality-Sensitive Hashing）—

一、前言

最近在工作中需要对海量数据进行相似性查找，即对微博全量用户进行关注相似度计算，计算得到每个用户关注相似度最高的TOP-N个用户，首先想到的是利用简单的协同过滤，先定义相似性度量（cos，Pearson,Jaccard），然后利用通过两两计算相似度，计算top-n进行筛选，这种方法的时间复杂度为\(O(n^2)\)（对于每个用户，都和其他任意一个用户进行了比较）但是在实际应用中，对于亿级的用户量，这个时间复杂度是无法忍受的。同时，对于高维稀疏数据，计算相似度同样很耗时，即\(O(n^2)\)的系数无法省略。这时，我们便需要一些近似算法，牺牲一些精度来提高计算效率，在这里简要介绍一下MinHashing，LSH，以及Simhash。

二、 MinHashing

Jaccard系数是常见的衡量两个向量（或集合）相似度的度量：

\[
J(A,B)=\frac {\left | A\cap B \right |}{\left | A\cup B \right |}
\]

为方便表示，我们令A和B的交集的元素数量设为\(x\)，A和B的非交集元素数量设为\(y\)，则Jaccard相似度即为\(）\frac x {(x+y）}\)。

所谓的MinHsah，即进行如下的操作：

对A、B的\(n\)个维度，做一个随机排列（即对索引\(，i_1,i_2,i_3,\cdots，i_n\)随机打乱）
分别取向量A、B的第一个非0行的索引值（\(index\)），即为MinHash值
得到AB的MinHash值后，可以有以下一个重要结论：
\[
P[minHash(A) = minHash(B)] = Jaccard（A,B）
\]

以下是证明：
在高维稀疏向量中，考虑AB在每一维的取值分为三类：

A、B均在这一维取1（对应上述元素个数为\(x\)）
A、B只有一个在这一维取1（对应上述元素个数为\(y\)）
A、B均取值为0

其中，第三类占绝大多数情况，而这种情况对MinHash值无影响，第一个非零行属于第一类的情况的概率为\(（）\frac x{（x+y）}\)，从而上面等式得证。
另外，按照排列组合的思想，全排列中第一行为第一类的情况为\(（）(x*（x+y-1）!)\)，全排列为\((x+y)!\)，即将\(n\)维向量全排列之后，对应的minHash值相等的次数即为Jaccard相似度。

但是在实际情况中，我们并不会做\((x+y)!\)次排列，只做\(m\)次（\(m\)一般为几百或者更小，通常远小于\(n\)），这样，将AB转为两个\(m\)维的向量，向量值为每次排列的MinHash值。
\[
sig(A)=[h_1(A),h_2(A),\cdots,h_m(A)]
\]

\[
sig(B)=[h_1(B),h_2(B),\cdots,h_m(B)]
\]

这样计算两个Sig向量相等的比例，即可以估计AB的Jaccard相似度（近似保持了AB的相似度，但是不能完全相等，除非全排列，对于这种利用相似变换相似空间的方法，需要设计哈希函数，而一般的哈希函数无法将满足相似向量哈希后的值相似）。
在实际实现中，m次排列通常通过一个针对索引的哈希来达到hash的效果，即MinHashing算法（实现可参考Spark实现细节
http://spark.apache.org/docs/2.2.0/api/java/org/apache/spark/ml/feature/MinHashLSH.html）

三、LSH

上面的MinHashing解决了高维稀疏向量的运算，但是计算两两用户的相似度，其时间复杂度仍然是O(n^2),显然这个计算量还没有得到改善，这时我们如果能将用户分到不同的桶，只比较可能相似的用户，即相似用户以较大可能分到同一个桶内，这样不相似的用户基本不会发生比较，降低计算复杂度，LSH即为这样的方法。

LSH方法基于这样的思想：在原空间中很近（相似）的两个点，经过LSH哈希函数的映射后，有很大概率它们的哈希是一样的；而两个离的很远（不相似）的两个点，映射后，它们的哈希值相等的概率很小。

基于这样的思想，LSH选择的哈希函数即需要满足下列性质：

对于高维空间的任意两点，\(，x，y\)：

如果\(d(x,y)≤R\)，则\(h(x)=h(y)\)的概率不小于\(P_1\)
如果\(d(x,y)≥cR\)，则\(h(x)=h(y)\)的概率不大于\(P_2\)。

其中，\(c>1,P_1>P_2\)。满足这样性质的哈希函数，被称为 \((R,cR,P1,P2)-sensive\)。

本文介绍的LSH方法基于MinHashing函数。

LSH将每一个向量分为几段，称之为band，如下图\(^6\)

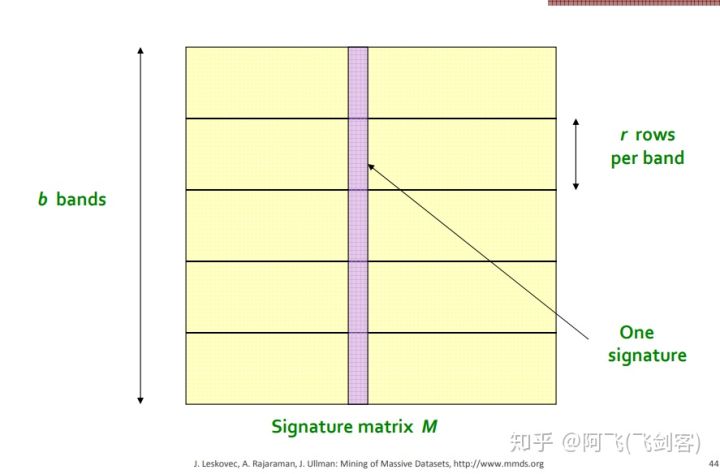
每一个向量在图中被分为了\(b\)段（每一列为一个向量），每一段有\(r\)行（个）MinHash值。在任意一个band中分到了同一个桶内，就成为候选相似用户（拥有较大可能相似）。

设两个向量的相似度为\(t\)，则其任意一个band所有行相同的概率为\(t^r\)，至少有一行不同的概率为\(1-t^r\), 则所有band都不同的概率为\(（）（1-t^r）^b\),至少有一个band相同的概率为\(（）1-（1-t^r）^b\)。其曲线如下图所示\(^6\)

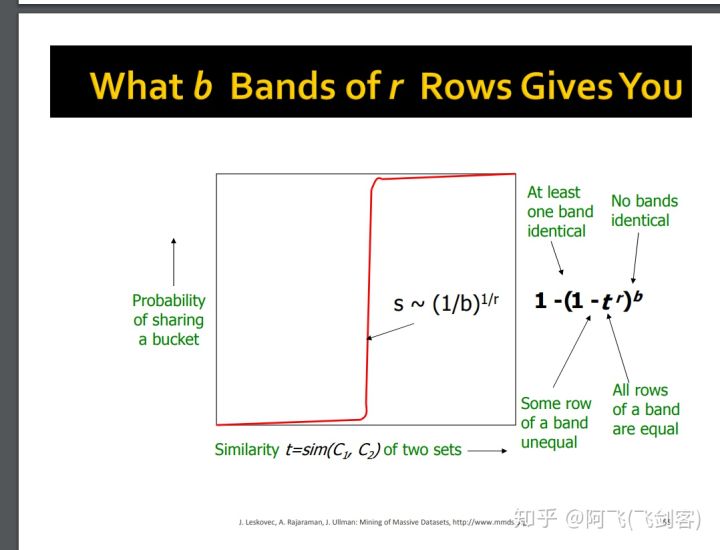
图中变化最抖的点s近似为\((\frac 1 b)^{\frac 1 r}\)，其中，s作为阈值为具体为多少是我们才将其分到一个桶中，即人工设定s来确定这里的b和r。如图例，对于\(r=5,b=10\)时，其阈值为0.6，其中，绿色为假正例率（相似度很低的两个用户被哈希到同一个桶内），蓝色为假负例率（真正相似的用户在每一个band上都没有被哈希到同一个桶内），可以设置\(，b，r\)调整\(s\)，\(s\)越大，效率越高，假正例率越低，假负例率越高。

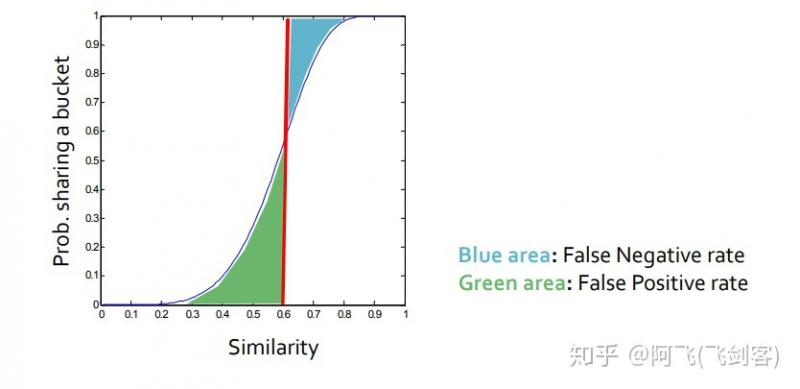
四、后记

接触LSH是一个很偶然的工作中的小需求，感慨其在海量高维稀疏数据中有很好的应用场景（文本，图片，结构数据均可以用），速度快，计算复杂度低，感慨其embedding转换的巧妙，鉴于本人水平和精力着实有限，没有搞懂的地方其实还很多，没有证明MinHashing方法满足LSH方法的性质，也没有搞懂BloomFilter算不算也是一种LSH方法的哈希函数。知乎用户@hunter7z的答案给了我不少的启发，感谢。
查了很多资料，作此读书笔记，权且抛砖引玉。

参考文献：

http://www.mmds.org/
https://zhuanlan.zhihu.com/p/46164294
http://spark.apache.org/docs/2.2.0/api/java/org/apache/spark/ml/feature/MinHashLSH.html
http://mlwiki.org/index.php/Locality_Sensitive_Hashing
https://www.cnblogs.com/wangguchangqing/p/9796226.html
http://www.mmds.org/mmds/v2.1/ch03-lsh.pdf

本文由飞剑客原创，如需转载，请联系私信联系知乎：@AndyChanCD