Joyful HDU - 5245 概率问题

Sakura has a very magical tool to paint walls. One day, kAc asked Sakura to paint a wall that looks like an M×NM×N matrix. The wall has M×NM×N squares in all. In the whole problem we denotes (x,y)(x,y) to be the square at the xx-th row, yy-th column. Once Sakura has determined two squares (x1,y1)(x1,y1) and (x2,y2)(x2,y2), she can use the magical tool to paint all the squares in the sub-matrix which has the given two squares as corners.

However, Sakura is a very naughty girl, so she just randomly uses the tool for KKtimes. More specifically, each time for Sakura to use that tool, she just randomly picks two squares from all the M×NM×N squares, with equal probability. Now, kAc wants to know the expected number of squares that will be painted eventually.

InputThe first line contains an integer TT(T≤100T≤100), denoting the number of test cases.

For each test case, there is only one line, with three integers M,NM,N and KK. 
It is guaranteed that 1≤M,N≤5001≤M,N≤500, 1≤K≤201≤K≤20. 
OutputFor each test case, output ''Case #t:'' to represent the tt-th case, and then output the expected number of squares that will be painted. Round to integers.Sample Input

2
3 3 1
4 4 2

Sample Output

Case #1: 4
Case #2: 8

Hint

The precise answer in the first test case is about 3.56790123.

题意：

给出一个M*N的矩阵，从其中任意的选两个格子，将以两个格子为对角的矩形染色。这样的操作重复k次，问会被涂色的格子数的期望值。

分析：

期望值说白了就是执行完上述操作后，计算最有可能涂了多少个格子。

看了网上的题解才明白，我们只需要计算每一个格子可能被选中的概率，

期望值E(x)=x1*p1 + x2*p2 + .....  + xn*pn;

在这里我们把每1个格子看做独立事件，所以这里的x1=x2=.....=xn=1，

所以对于本题，期望值 E(x)=p1 + p2 + .....  + pn;

解题：

现在问题就简化成了求 每一个格子 被选中的概率，再累加即可。

先看一张图：

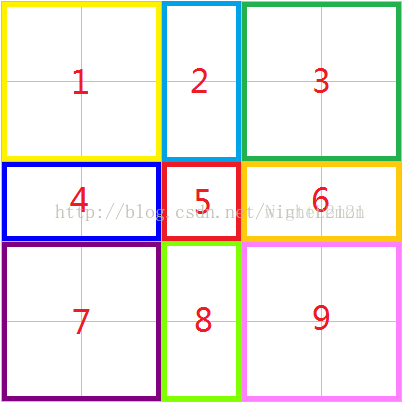
假设现在我们求5这个点被涂色的概率，怎样可以让他染上色呢？

选点（x1,y1）和 （x2,y2）构成的矩形包含5这个点即可。

在矩阵中选两个点的总情况数 是 m*n * m*n

那么选点有9种情况：

1、若(x1,y1)在区域1，则(x2,y2)可以在区域5、6、8、9

2、若(x1,y1)在区域3，则(x2,y2)可以在区域4、5、7、8

3、若(x1,y1)在区域7，则(x2,y2)可以在区域2、3、5、6

4、若(x1,y1)在区域9，则(x2,y2)可以在区域1、2、4、5

5、若(x1,y1)在区域2，则(x2,y2)可以在区域4、5、6、7、8、9

6、若(x1,y1)在区域4，则(x2,y2)可以在区域2、3、5、6、8、9

7、若(x1,y1)在区域6，则(x2,y2)可以在区域1、2、4、5、7、8

8、若(x1,y1)在区域8，则(x2,y2)可以在区域1、2、3、4、5、6

9、若(x1,y1)在区域5，则(x2,y2)可以在任意区域

当前这个点被染色的概率就是这9种情况之概率和。
---------------------

参考博客：https://blog.csdn.net/winter2121/article/details/71082686

#include <map>
#include <set>
#include <stack>
#include <cmath>
#include <queue>
#include <cstdio>
#include <vector>
#include <string>
#include <bitset>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <algorithm>
#define ls (r<<1)
#define rs (r<<1|1)
#define debug(a) cout << #a << " " << a << endl
using namespace std;
typedef long long ll;
const ll maxn = 1e3+10;
const ll mod = 1e9+7;
const double pi = acos(-1.0);
const double eps = 1e-8;
int main() {
    ll T, k;
    double n, m;
    scanf("%lld",&T);
    for( ll cas = 1; cas <= T; cas ++ ) {
        scanf("%lf %lf %lld",&m,&n,&k);
        double sum = n*m*n*m, ans = 0; //sum：所有的情况种数，ans：期望值
        for( ll i = 1; i <= m; i ++ ) {
            for( ll j = 1; j <= n; j ++ ) { //对每一个点算贡献值
                double p = 0; //点(i,j)被选中的情况数
　　　　　　　　//另外一个点在区域1，3，5，7
                p += (i-1)*(j-1)*(m-i+1)*(n-j+1);
                p += (i-1)*(n-j)*(m-i+1)*j;
                p += (m-i)*(j-1)*i*(n-j+1);
                p += (m-i)*(n-j)*i*j;
　　　　　　　　//另外一个点在区域2，4，6，8　
                p += (i-1)*1*(m-i+1)*n;
                p += 1*(j-1)*m*(n-j+1);
                p += 1*(n-j)*m*j;
                p += (m-i)*1*i*n;
　　　　　　　　//另外一个点在区域5
                p += m*n;
　　　　　　　　//点(i,j)被选中的概率
                p = (p*1.0)/sum;
                ans += 1-pow(1-p,k);
            }
        }
        printf("Case #%lld: %.0f\n",cas,ans);
    }
    return 0;
}