计算几何 val.1

目录

• 计算几何 val.1
  • 向量的点积
  • 向量的叉积
  • 一种奇怪的三角剖分求面积
  • 凸包
  • 点绕点旋转
  • 后记

计算几何 val.1

本文并不是入门文章，供有高中数学基础的阅读

主要写一些重要的点和注意事项吧

向量的点积

• 如果两个向量同向（共线），那么它们的数量积为他们的模长之积。
• 如果两个向量夹角 \(<90^\circ\) ，那么它们的数量积为正。
• 如果两个向量夹角 \(=90^\circ\) ，那么他们的数量积为 \(0\) 。
• 如果两个向量夹角 \(>90^\circ\) ，那么它们的数量积为负。
• 如果两个向量反向（共线），那么它们的数量积为他们的模长之积的相反数

这个可以判断它们的夹角

向量的叉积

几何意义：两向量由平行四边形法则围成的面积

叉乘满足的基本的性质如下:

1. \(\vec{a}×\vec{a}=0\) 因为夹角是0, 所以平行四边形面积也是0, 即叉积长度为0
2. \(\vec{a}×\vec{b}=−(\vec{b}×\vec{a})\), 等式两边的叉积等大反向, 模长因为平行四边形不变而相同, 方向因为右手法则旋转方向相反而相反
3. \((λ\vec{a})×\vec{b}=λ(\vec{a}×\vec{b})\), 这点比较好想, 因为: ①正数λλ数量乘不会影响a的方向, 所以左右的叉积方向一样; 负数\(λ\)使得\(a\)反向了, 但也使得左右叉积方向相反. ②对a进行缩放, 平行四边形面积也同等缩放.
4. \((\vec{a}+\vec{b})×\vec{c}=\vec{a}×\vec{c}+\vec{b}×\vec{c}\)

\(\vec{a}×\vec{b}\) 的正负可以理解为 \(\vec{a}\)转到\(\vec{b}\)的逆时针形成的角，\(\leq \pi\)为正，否则为负

可以判断一些东西（凸包），求距离

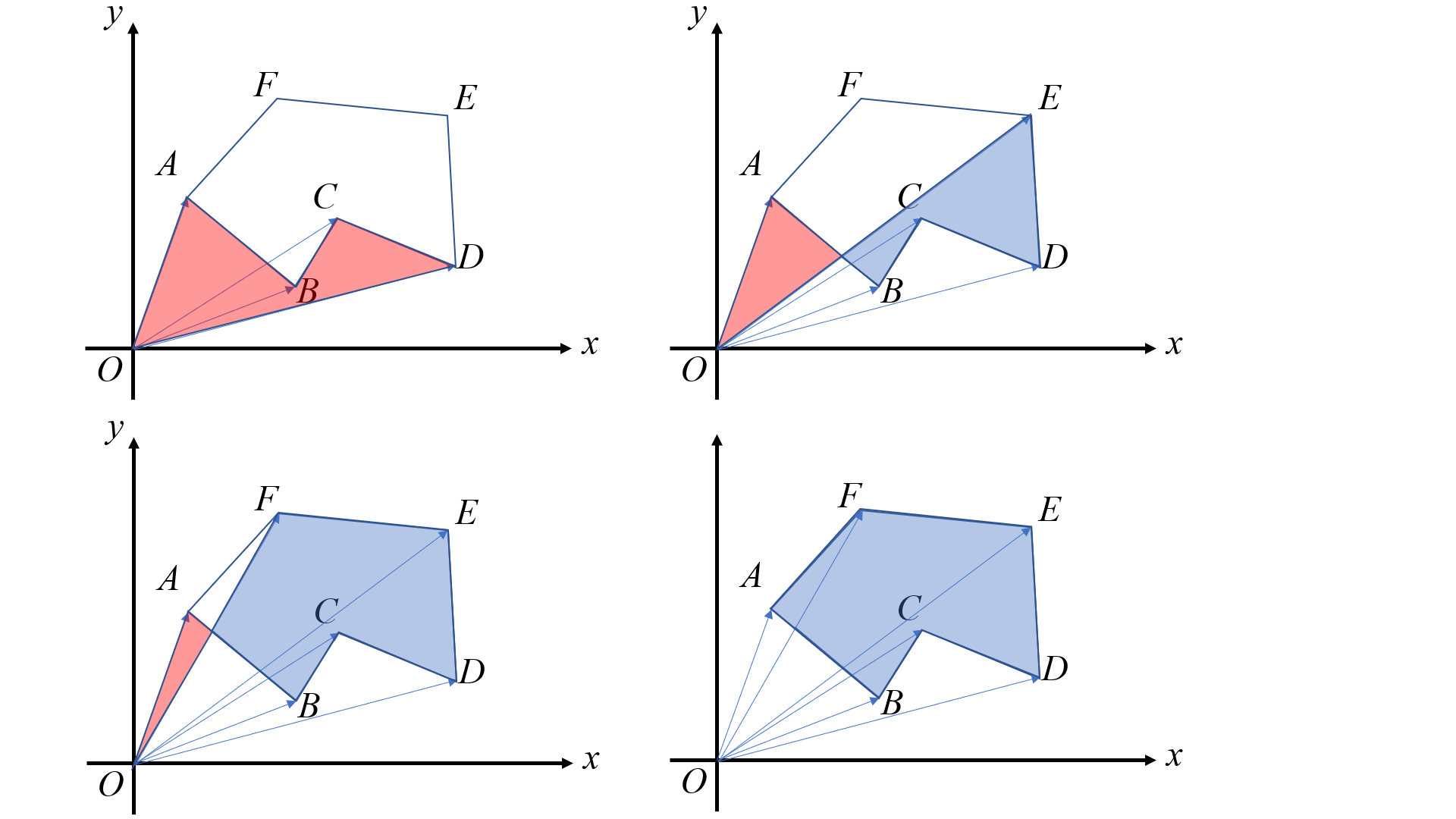
一种奇怪的三角剖分求面积

在这里学到的

\(S_{ABCDEF}=\frac{\overrightarrow{OA}\times \overrightarrow{OB}+\overrightarrow{OB}\times \overrightarrow{OC}+\dots +\overrightarrow{OF}\times \overrightarrow{OA}}{2}\)

凸包

用最少的周长覆盖所有点的多边形

性质：一定没有凹陷（可以用叉积判了）

叉积坐标公式的证明：

设

\[T_1=\sqrt{x_1^2+y_1^2},T_2=\sqrt{x_2^2+y_2^2}
\]

则

\[S=T_1*T_2*\sin\theta=\sin\alpha-\beta=\sin\alpha\cos\beta-\cos\alpha\sin\beta
\]

\[=(\frac{y_2}{T_2}*\frac{x_1}{T_1}-\frac{x_2}{T_2}*\frac{y_1}{T_1})*T_1*T_2
\]

\[=x_1*y_2-y_1*x_2
\]

具体方法是先求下凸壳然后再求上凸壳，注意一号点要进去两次比较最后一个点和第一个点，来判断是否弹出最后加进去的点

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
struct point{
	double x,y;
	double operator * (point b){
		return x*b.y-y*b.x;
	}
	point operator - (point b){
		point re;re.x=x-b.x,re.y=y-b.y;return re;
	}
	point operator + (point b){
		point re;re.x=x+b.x,re.y=y+b.y;return re;
	}
	double dis(){
		return sqrt(x*x+y*y);
	}
};
const int N = 10021;
point p[N],h[N];
int cmp(point a,point b){
	return a.x==b.x?a.y<b.y:a.x<b.x;
}
int n;
int stk[N],tp=0,used[N];
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%lf%lf",&p[i].x,&p[i].y);
	}
	sort(p+1,p+n+1,cmp);
	stk[++tp]=1;
	for(int i=2;i<=n;i++){
		while( tp>1 && (p[stk[tp]]-p[stk[tp-1]])*(p[i]-p[stk[tp]]) <=0 ) used[stk[tp--]]=0;//小于等于为去除凸包边上的点
		used[i]=1;
		stk[++tp]=i;
	}//下凸壳
	int ntp=tp;
	for(int i=n-1;i>=1;i--){
		if(!used[i]){
			while(tp>ntp&&(p[stk[tp]]-p[stk[tp-1]])*(p[i]-p[stk[tp]])<=0){
				used[stk[tp--]]=0;
			}
			used[i]=1;
			stk[++tp]=i;
		}
	}//上凸壳
	for(int i=1;i<=tp;i++){
		h[i]=p[stk[i]];
	}//tp和1是同一点
	double ans=0;
	for(int i=2;i<=tp;i++){
		ans+=(h[i]-h[i-1]).dis();
	}
	printf("%.2f",ans);
	return 0;
}

点绕点旋转

考虑成 点+向量之差等于要求的点

向量之差也等于绕中心旋转的向量的差，三角恒等变换算一算就行

后记

就先这么多吧。。。

明天目标：旋转卡壳+半平面交