matlib实现梯度下降法

样本文件下载：ex2Data.zip

ex2x.dat文件中是一些2-8岁孩子的年龄。

ex2y.dat文件中是这些孩子相对应的体重。

我们尝试用批量梯度下降法，随机梯度下降法和小批量梯度下降法来对这些数据进行线性回归，线性回归原理在：http://www.cnblogs.com/mikewolf2002/p/7560748.html

1.批量梯度下降法（BGD)

BGD.m代码：

clear all; close all; clc;
x = load('ex2x.dat'); %装入样本输入特征数据到x，年龄
y = load('ex2y.dat'); %装入样本输出结果数据到y，身高
figure('name','线性回归-批量梯度下降法');
plot(x,y,'o') %把样本在二维坐标上画出来
xlabel('年龄') %x轴说明
ylabel('身高')  %y轴说明

m = length(y); % 样本数目
x = [ones(m, 1), x]; % 输入特征增加一列，x0=1
theta = zeros(size(x(1,:)))'; % 初始化theta

MAX_ITR = 1500;%最大迭代数目
alpha = 0.07; %学习率
i = 0;
while(i<MAX_ITR)
   grad = (1/m).* x' * ((x * theta) - y);%求出梯度
   theta = theta - alpha .* grad;%更新theta
   if(i>2)
       delta = old_theta-theta;
       delta_v = delta.*delta;
       if(delta_v<0.000000000000001)%如果两次theta的内积变化很小，退出迭代
           break;
       end
   end
   old_theta = theta;
   i=i+1;
end
i
theta
predict1 = [1, 3.5] *theta
predict2 = [1, 7] *theta
hold on
plot(x(:,2), x*theta, '-') % x现在是一个2列的矩阵
legend('训练数据', '线性回归')%标记每个数据设置

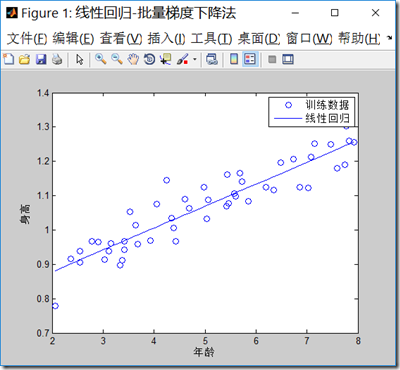
程序输结果如下：迭代次数达到了上限1500次，最后梯度下降法求解的theta值为\([0.7502,0.0639]^T\)，两个预测值3.5岁，预测身高为0.9737米，7岁预测为1.1973米。

注意学习率的选择很重要，如果选择太大，可能不能得到收敛的\(\theta\)值。

i =

        1500

theta =

    0.7502
    0.0639

predict1 =

    0.9737

predict2 =

    1.1973

2.随机梯度下降法

sgd.m代码如下，注意最大迭代次数增加到了15000，1500次迭代不能得到收敛的点，可见随机梯度下降法，虽然计算梯度时候，工作量减小，但是因为不是最佳的梯度下降方向，可能会使得迭代次数增加：

clear all; close all; clc;
x = load('ex2x.dat');
y = load('ex2y.dat');
figure('name','线性回归-随机梯度下降法');
plot(x,y,'o')
xlabel('年龄') %x轴说明
ylabel('身高')  %y轴说明
m = length(y); % 样本数目
x = [ones(m, 1), x]; % 输入特征增加一列
theta = zeros(size(x(1,:)))';%初始化theta

MAX_ITR = 15000;%最大迭代数目
alpha = 0.01;%学习率
i = 0;
while(i<MAX_ITR)
   %j = unidrnd(m);%产生一个最大值为m的随机正整数j，j为1到m之间
   j = mod(i,m)+1;
   %注意梯度的计算方式，每次只取一个样本数据，通过轮转的方式取到每一个样本。
   grad =  ((x(j,:)* theta) - y(j)).*x(j,:)';
   theta = theta - alpha * grad;
   if(i>2)
      delta = old_theta-theta;
      delta_v = delta.*delta;
      if(delta_v<0.0000000000000000001)
          break;
      end
   end
   old_theta = theta;
   i=i+1;
end
i
theta
predict1 = [1, 3.5] *theta
predict2 = [1, 7] *theta
hold on
plot(x(:,2), x*theta, '-')
legend('训练数据', '线性回归')

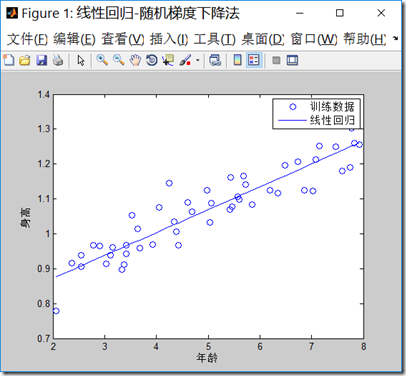
程序结果输出如下：

i =

       15000

theta =

    0.7406
    0.0657

predict1 =

    0.9704

predict2 =

    1.2001

3.小批量梯度下降法

mbgd.m代码如下，程序中批量的样本数目，我们选择5：

clear all; close all; clc;
x = load('ex2x.dat');
y = load('ex2y.dat');
figure('name','线性回归-小批量梯度下降法')
plot(x,y,'o')
xlabel('年龄') %x轴说明
ylabel('身高')  %y轴说明
m = length(y); % 样本数目

x = [ones(m, 1), x]; % 输入特征增加一列
theta = zeros(size(x(1,:)))'; %初始化theta

MAX_ITR = 15000;%最大迭代数目
alpha = 0.01;%学习率
i = 0;
b = 5; %小批量的数目
while(i<MAX_ITR)
   j = mod(i,m-b)+1;
   %每次计算梯度时候，只考虑b个样本数据
   grad = (1/b).*x(j:j+b,:)'*((x(j:j+b,:)* theta) - y(j:j+b));
   theta = theta - alpha * grad;
   if(i>2)
      delta = old_theta-theta;
      delta_v = delta.*delta;
      if(delta_v<0.0000000000000000001)
          break;
      end
   end
   old_theta = theta;
   i=i+b;
end
i
theta
predict1 = [1, 3.5] *theta
predict2 = [1, 7] *theta
hold on
plot(x(:,2), x*theta, '-')
legend('训练数据', '线性回归')

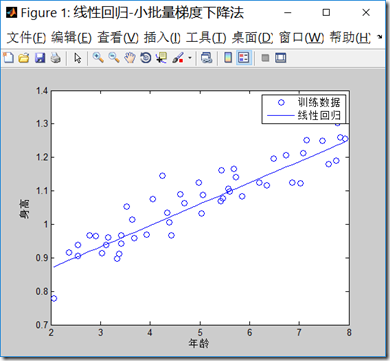
程序的输出结果：

i =

       15000

theta =

    0.7418
    0.0637

predict1 =

    0.9647

predict2 =

    1.1875