第二章 若依JFlow流程模型设计

若依-JFlow框架如何拉取、配置并运行请查看这篇文章：《第一章 若依-JFlow的配置与启动》

上一节我们讲解了如何拉取若依-JFlow框架代码并配置运行，这一部分我们就以公司员工请假的流程为例，设计一个流程，并为初始节点设计一个表单。

一、新建业务场景和流程模型

1. 启动项目以后，登录管理员账号（用户名：admin，密码：admin123），进入系统首页：

2. 创建流程：点击左侧第二个JFlow流程设计，再点击流程模板：

3. 系统中，流程树已经定义了一些业务场景（即不同的文件夹）如下图所示：

和文件夹的创建方式一样，我们只需要鼠标右键，点击新建子级目录即可创建一个业务场景，如果需要删除，就点击删除目录即可：

这里我创建一个名为业务场景231204的业务场景：

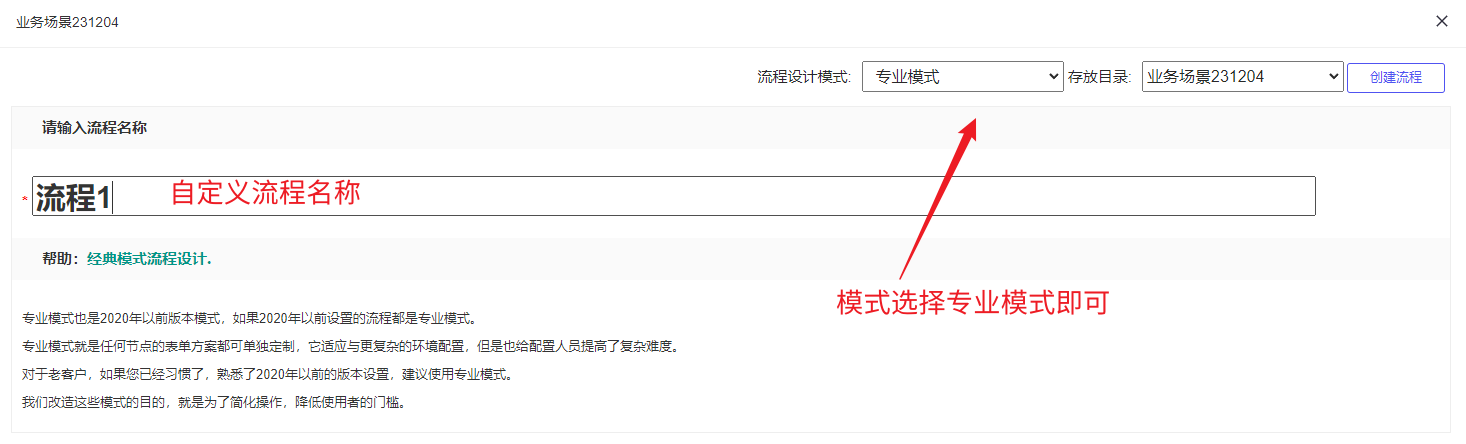
4. 创建流程模型：点击右上角新建流程

5. 流程名称自定义，设计模式选择专业模式即可，完成后点击右上角创建流程：

如果此时创建完成后，浏览器对弹出窗口拦截时，直接点击拦截窗口，选择始终允许弹出窗口并从http://localhost:8089重定向，然后点击完成即可：

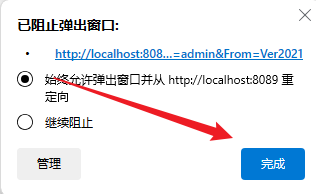
6. 此时就会弹出一个流程设计的窗口：

设计流程一共有五个步骤：

1. 绘制流程图
2. 设置接收人规则
3. 设计表单
4. 检查流程
5. 测试并运行该流程

二、绘制流程图

1. 一个流程是由一个个流程节点组成的，如下图所示，Start Node和Node 2都是这个流程图的节点，绿色标志的是开始节点：

2. 鼠标右键点击空白处，可以新建节点：

3. 双击某个节点可以修改该节点的名称：

4. 要想将两个节点连接起来，长按该节点的图标，然后将连接线拉向另一个节点：

当然，如果你需要对连接线上添加文字说明，双击连接线即可：

如需删除连接线，也需要双击连接线，点击删除即可：

以下是一个简单的请假的流程模型：

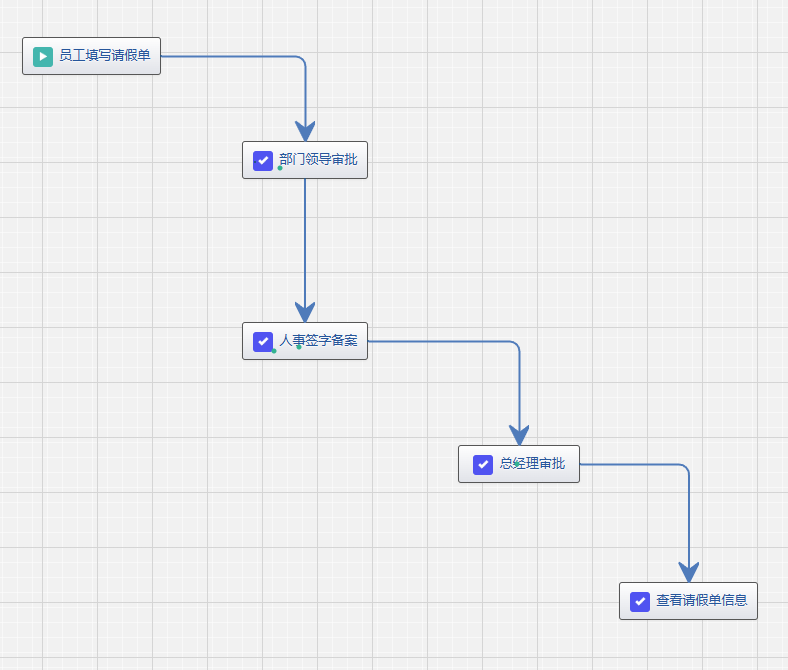
三、设置接收人规则

接收人规则是指当前节点完成任务以后，这个任务转到下一节点时，由谁来处理。

JFlow默认的处理规则是：上一个节点选择那一个人（或者部门），就由这个人（部门）来处理。当然，我们也可以自行设计接收人规则。

鼠标右键点击节点，选择节点属性

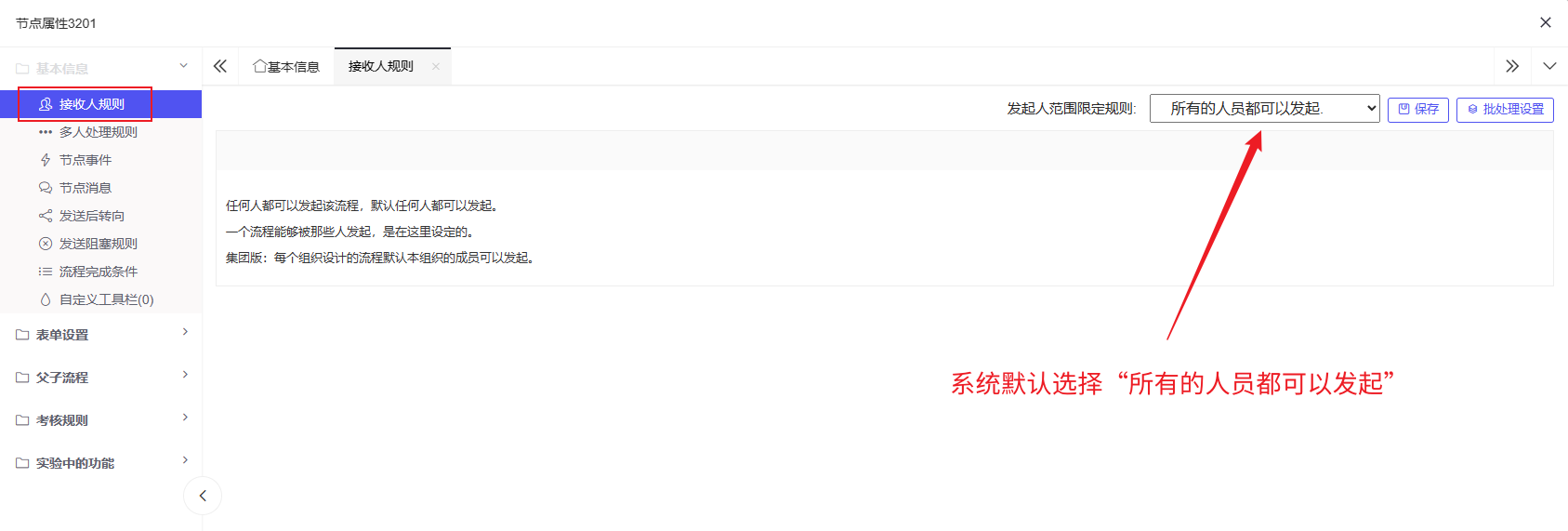
接下来，我们就按照正常的请假流程设置每一个节点的接收人规则：

1. 员工填写请假单：我们假设公司所有的员工都可以填写请假单，因此规则设定为：所有的人员都可以发起：

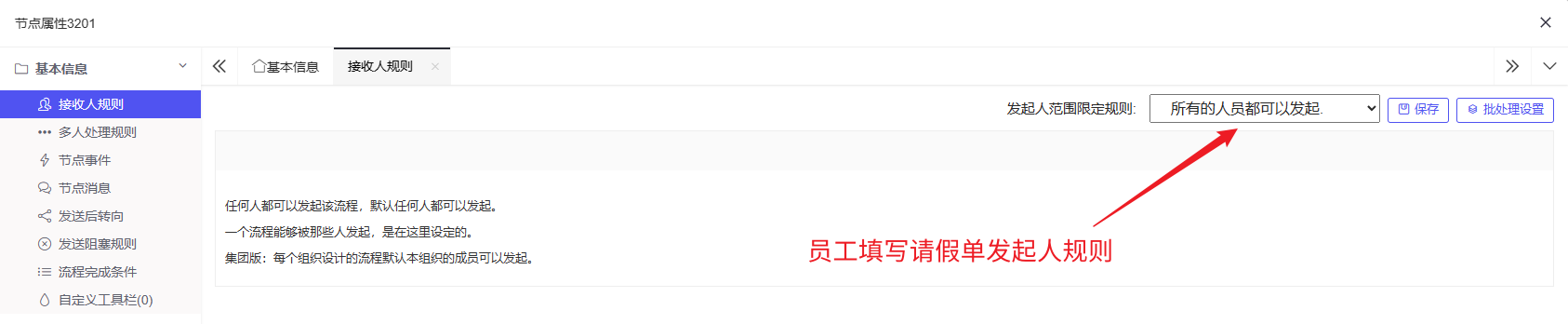
2. 部门领导审批：假设每一个员工都处于一个部门，那么员工要将请假单交给对应部门领导审批：

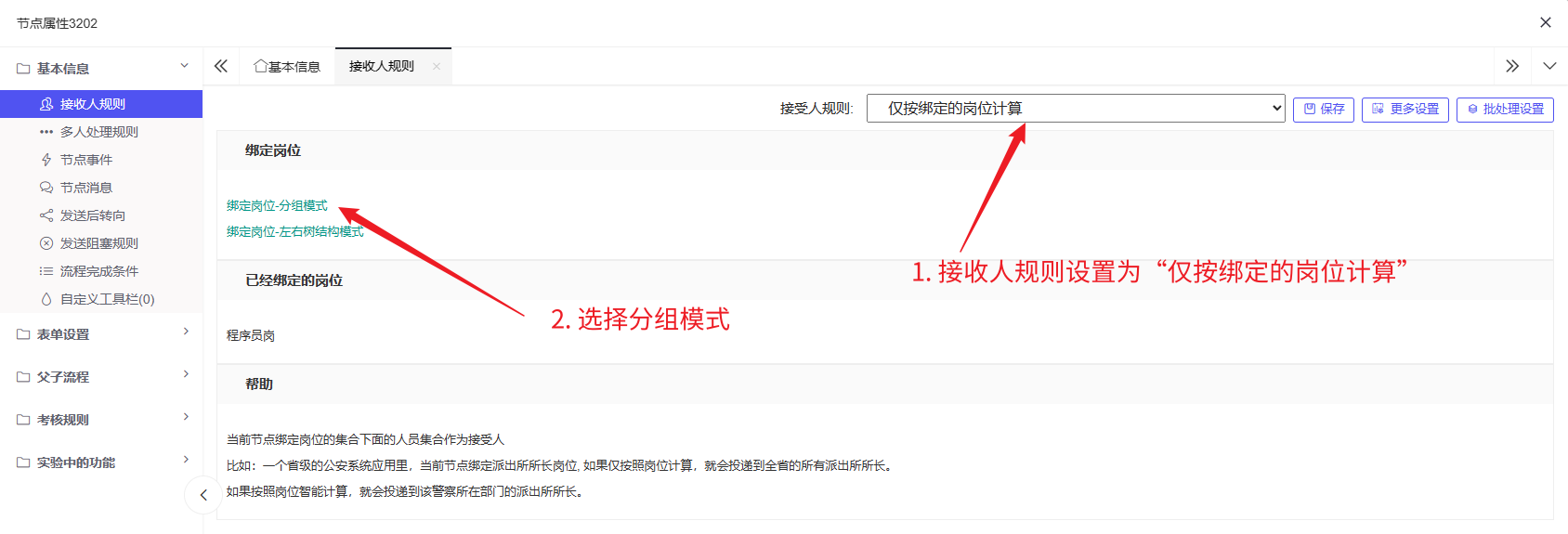
假设部门领导角色是开发组长，这里选择程序员，点击保存，然后关闭此窗口：

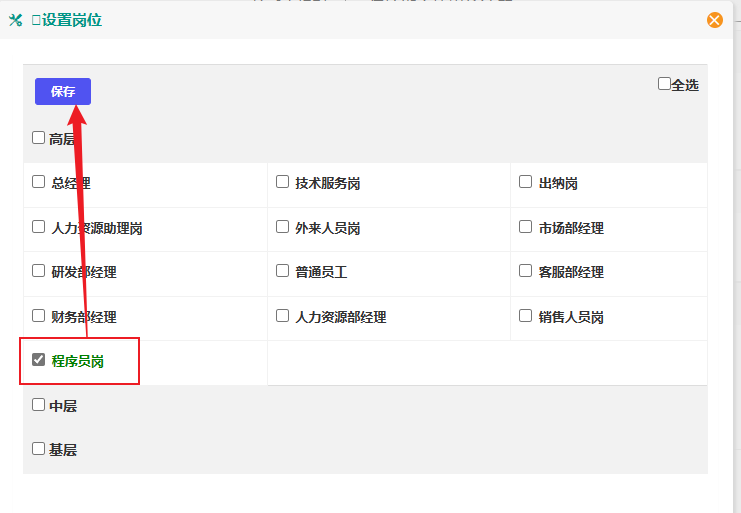
接收人规则页面也点击保存即可：

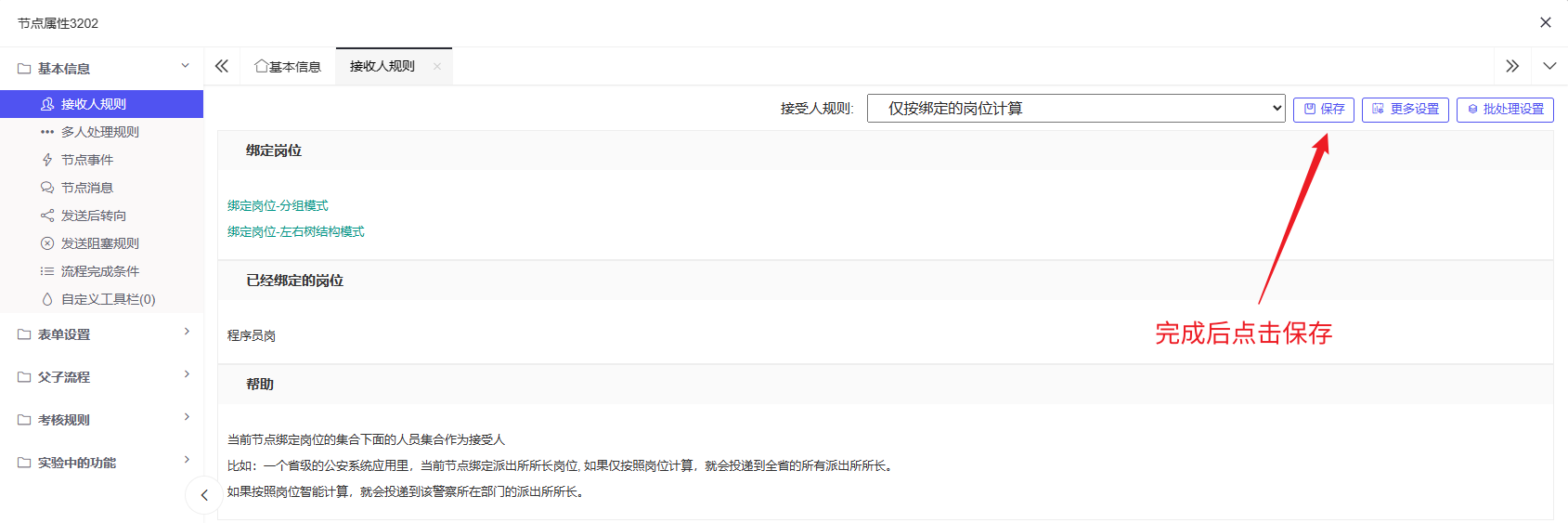
3. 人事签字备案：设置规则和部门领导审批基本相同，分组模式中选择人力资源部经理审批即可：

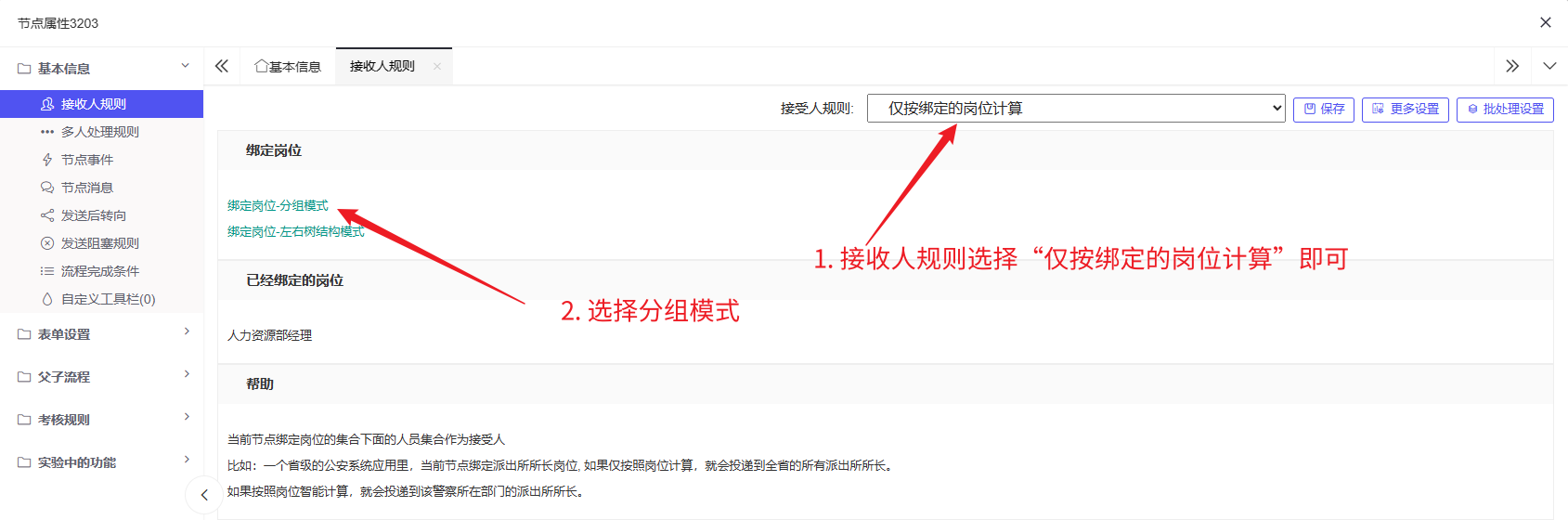
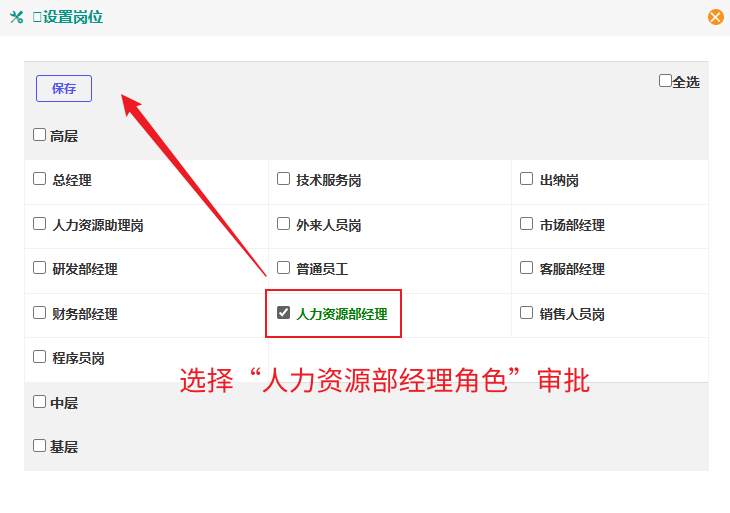
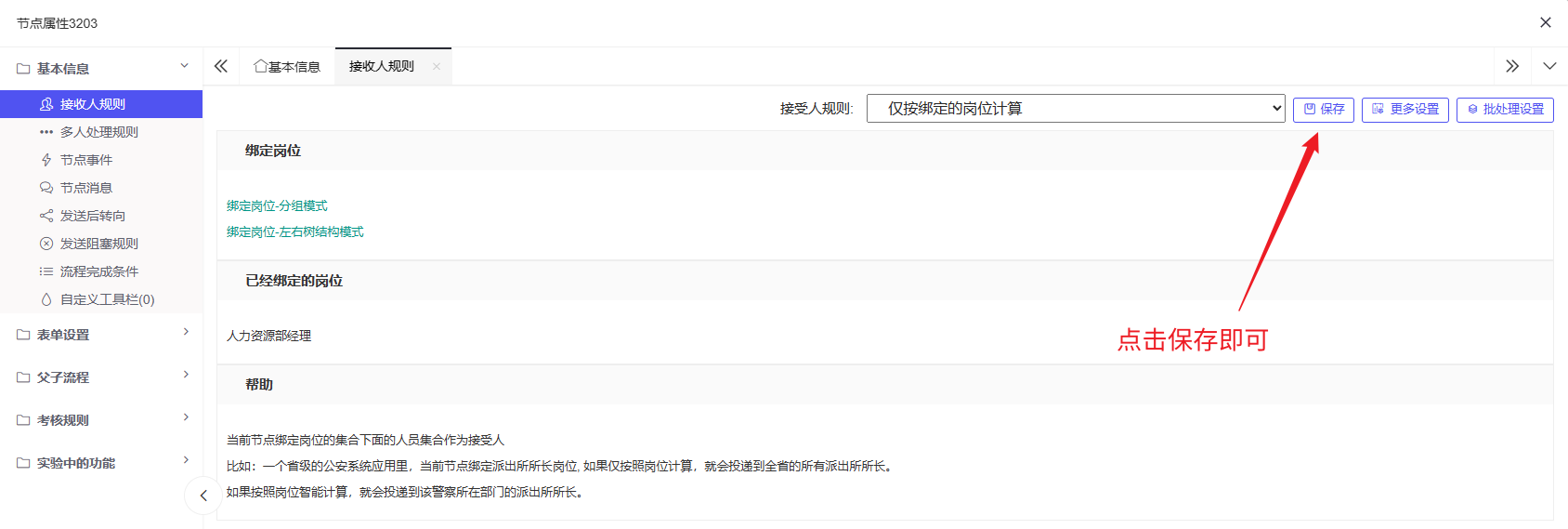
4. 总经理审批亦同理，分组模式中选择总经理审批即可：

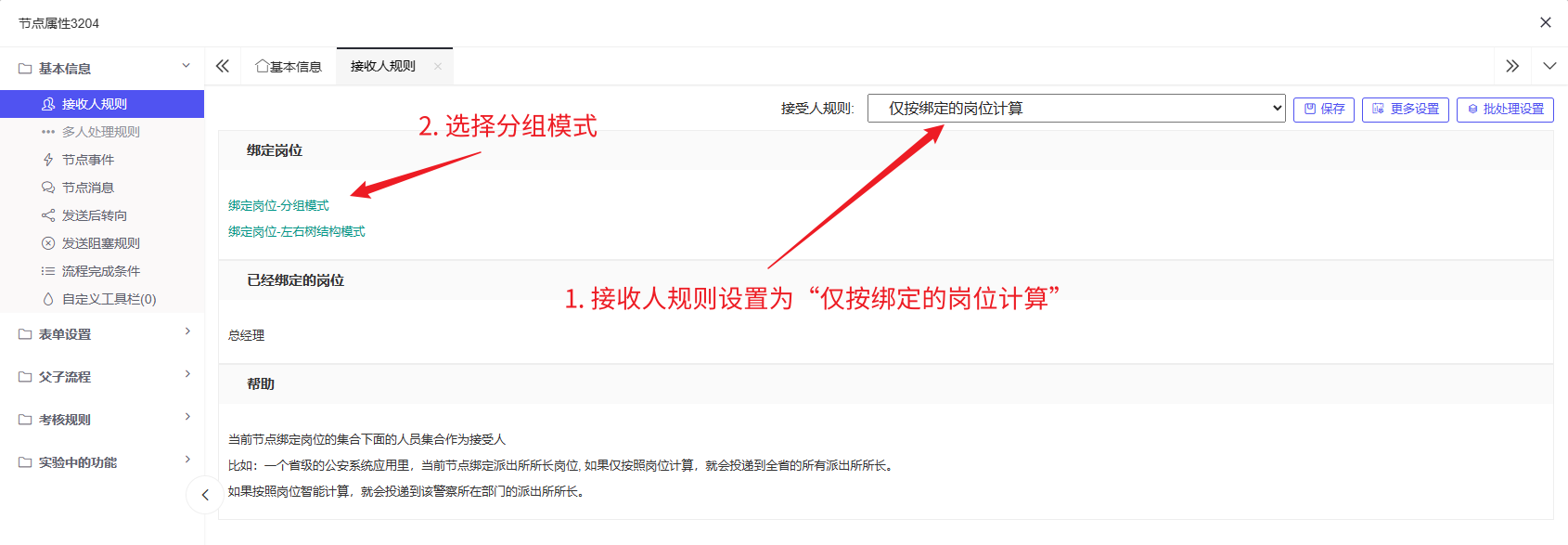
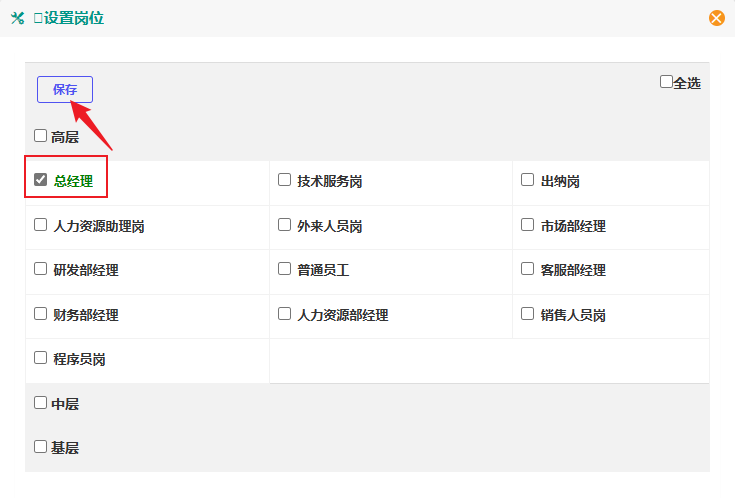
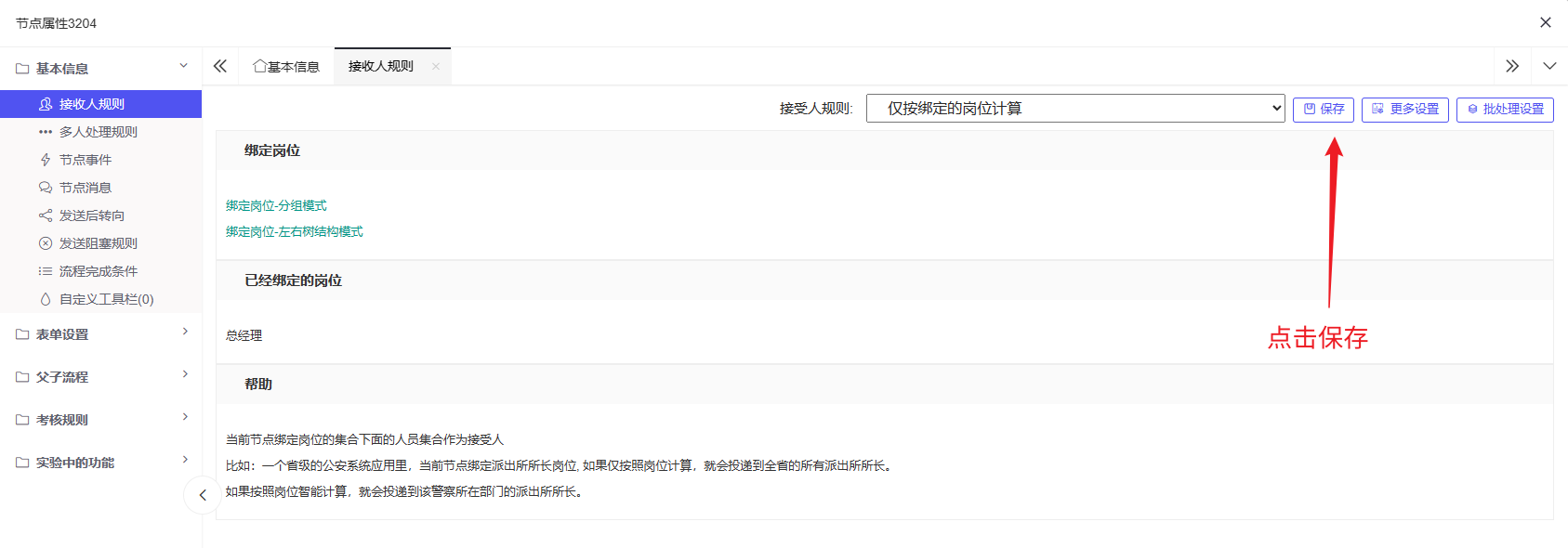
5. 查看请假单信息：由于是公司员工发起的请假申请，因此查看请假单信息应该由开始节点员工对应

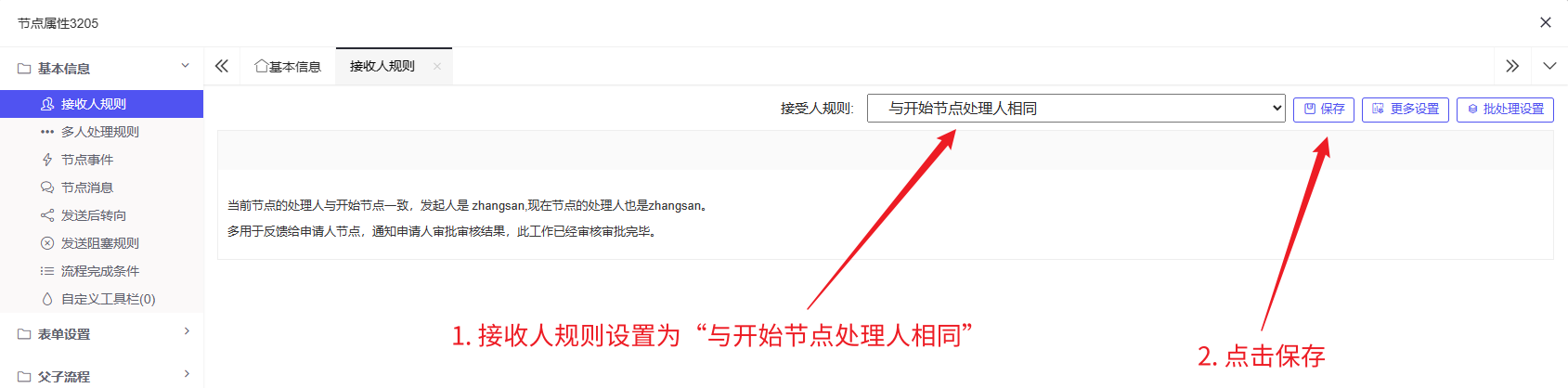
至此，整个请假流程的所有接收人规则设置完成。

四、设计单个节点表单

4.1 表单方案的说明

鼠标右键点击节点，点击表单方案。

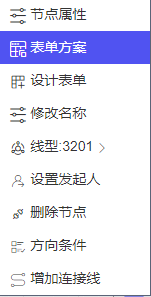
系统默认给我们提供的是傻瓜表单。

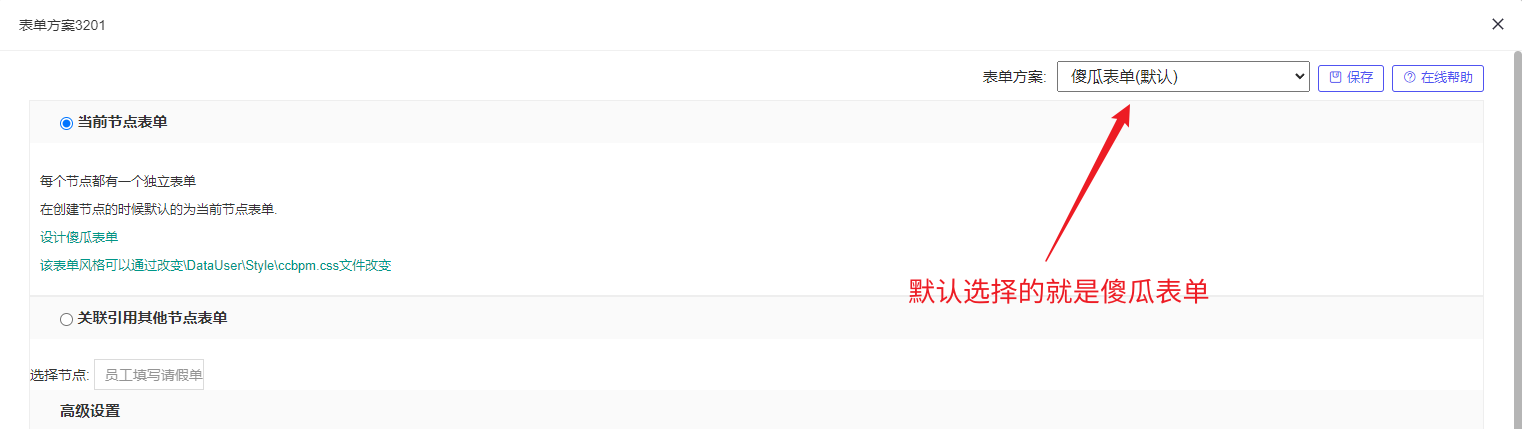
傻瓜表单指的是在一个表单中，对应一个标签和一个控件，例如：如果标签为姓名，那么控件对应的就是文本框；如果填写的是性别，那么需要填写的控件是单选框。

对于小白而言，选择傻瓜表单即可应对多种场景。当然，JFlow还为我们提供了更多的表单方案：

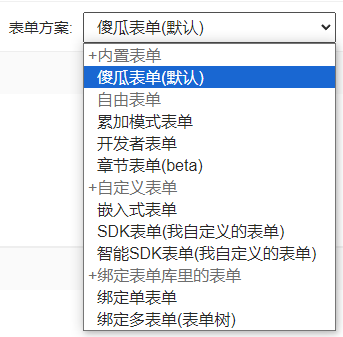
4.2 请假单页面分析与设计

接下来，我们就是用表单方案，设计各级角色的请假申请单。

1. 员工填写请假单：鼠标右键点击节点，选择设计表单。进入表单设计页面：

2. 对于申请人而言，需要填写申请人姓名、所在部门名称、申请日期、请假类别（例如：事假、病假、婚假、丧假等）、请假事由、请假开始时间、请假结束时间、请假时长计算。

• 对于申请人姓名、所在部门名称、申请日期我们只需要保证能获取到当前登录用户的信息和填写申请所在日期即可，直接让系统自动生成，不需要人为填写。
• 请假类别对应的控件需要设置成单选框（假设请假只有一种情况）。
• 请假开始时间、结束时间需要使用时间输入框。并且开始时间必须保证是今天及之后，结束时间必须是开始时间及之后。
• 请假时长需要根据请假时间开始时间和请假结束时间计算即可。

4.3 绘制请假单基本框架

按照前面对请假单页面的分析，绘制请假单。

1. 申请人姓名：在左侧组件的基本字段中选中文字框拖入到中间区域，此时弹出一个提示框，这里我们组件名称为申请人姓名，组件id按照系统默认生成的即可，完成后点击继续添加：

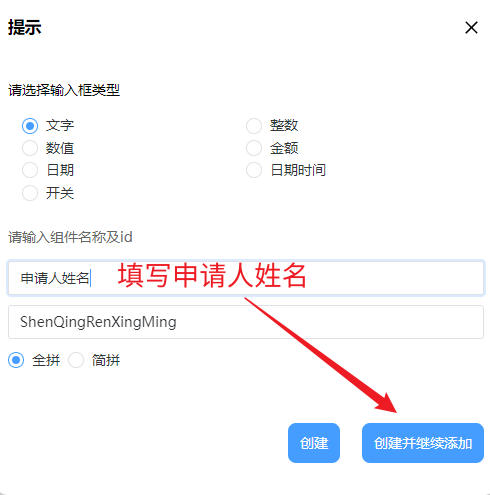
2. 接下来组件名称填写为申请人所在部门，然后点击创建并继续添加：

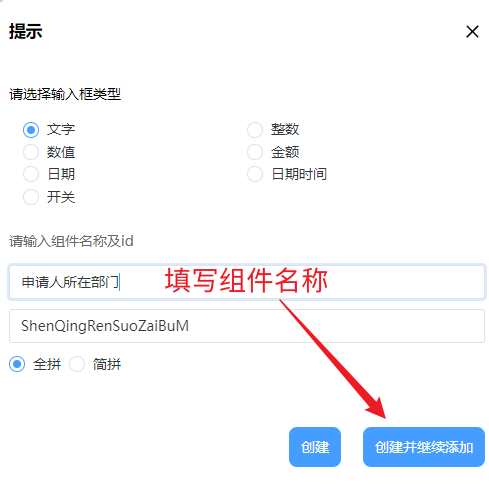
3. 申请日期的输入框类型是日期类型，然后填写组件名称，然后点击创建即可：

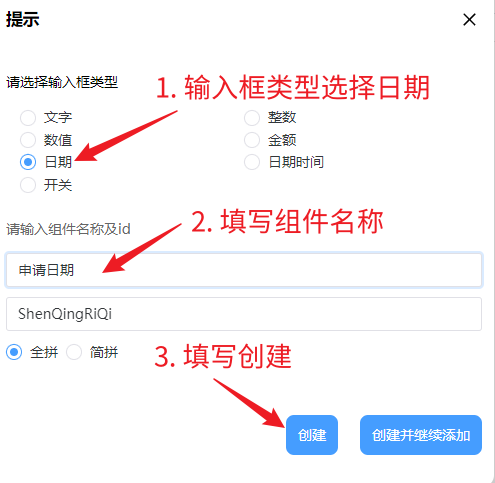
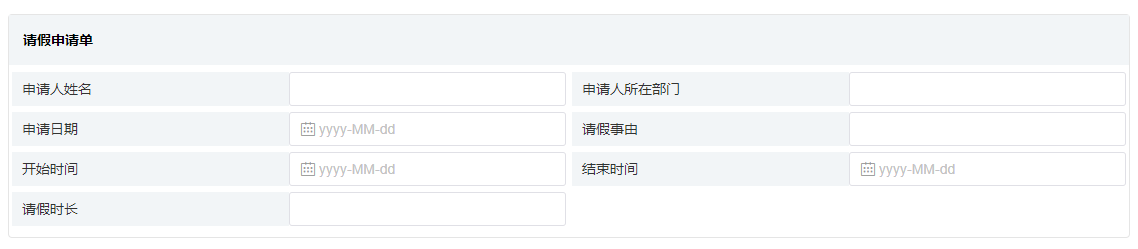
4. 此时表单如下图所示：

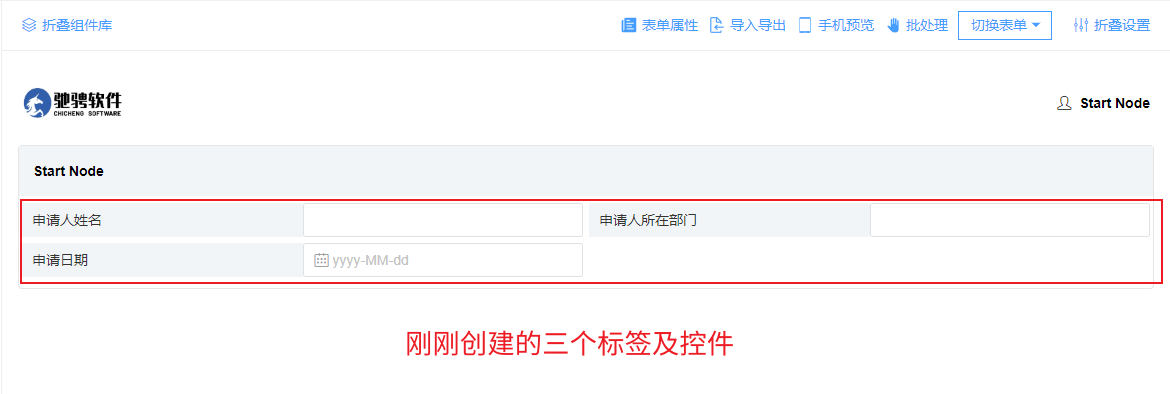
5. 请假事由是一个文本框，将左面文字组件拖入到表单即可：

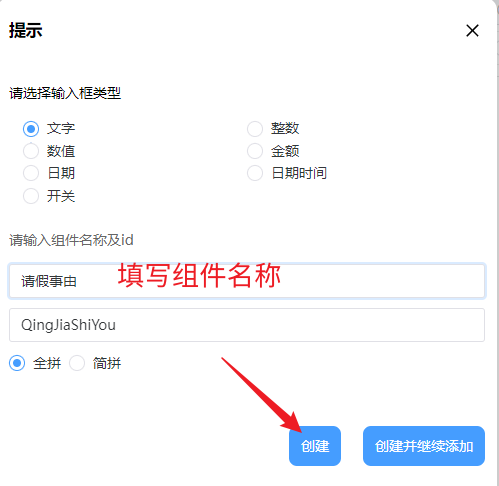
6. 添加请假开始时间和请假结束时间，选择日期组件，输入格式设定为日期即可：

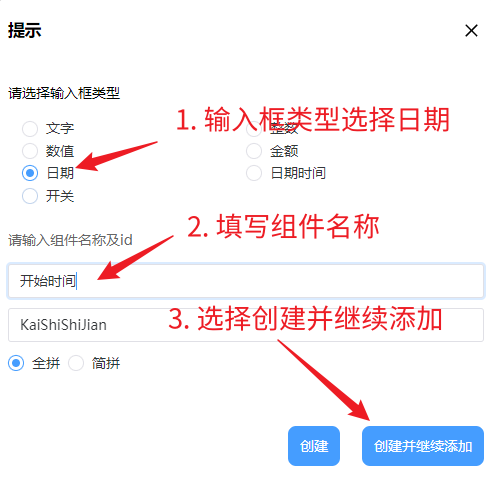
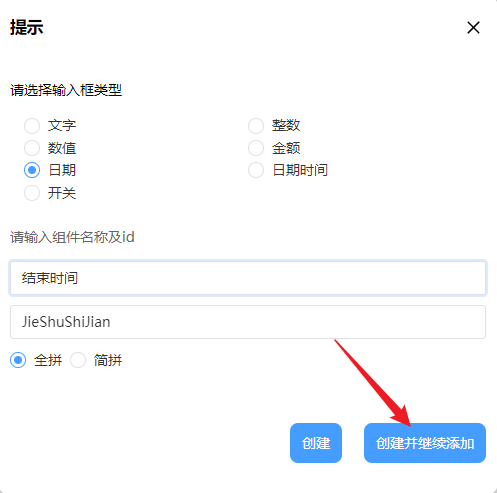
7. 请假时长控件的输入框类型选择数值即可：

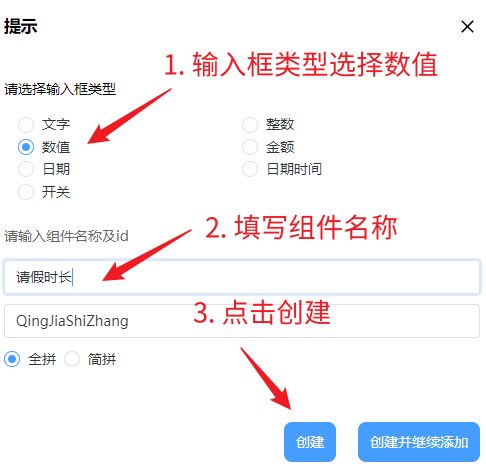
8. 至此，我们的请假单基本框架就绘制完成了，如下图所示：

4.4 对请假单进一步完善

1. 按照上面我们指定的要求：申请人姓名、所在部门、申请日期由系统自动生成，并且设置为只读。那么我们需要对这三个控件分别操作。

• 首先，点击申请人姓名，点击小齿轮，进入组件设置：

• 我们能看到当前组件的基本信息，将系统默认值设置为登陆人员名称，然后点击保存，然后关闭这个窗口即可。

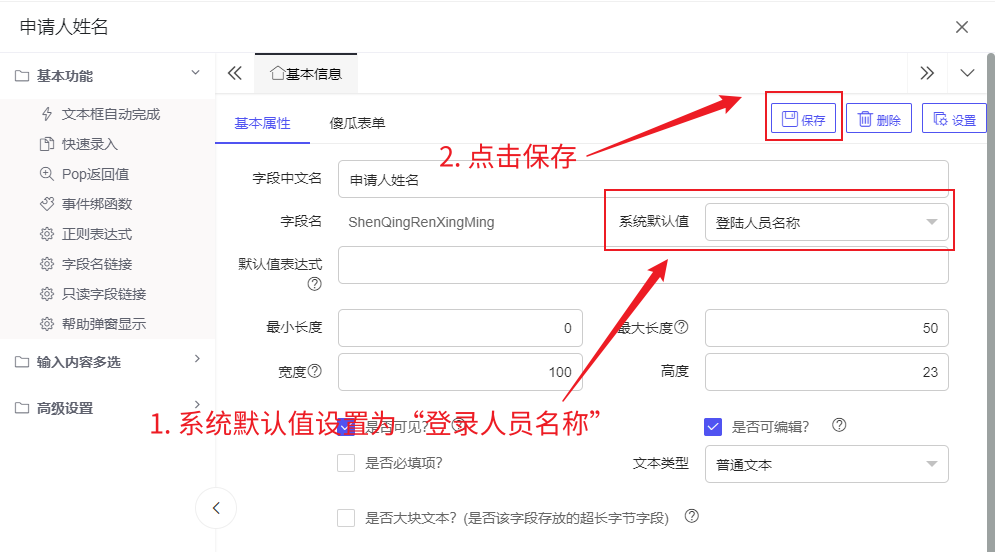
• 此时申请人姓名组件中文本框出现一个@WebUser.Name的标识，这是我们上一步设置的结果，不用修改。

• 申请人所在部门的设置和申请人姓名设置基本相同，只不过将系统默认值改为登陆人员部门名称：

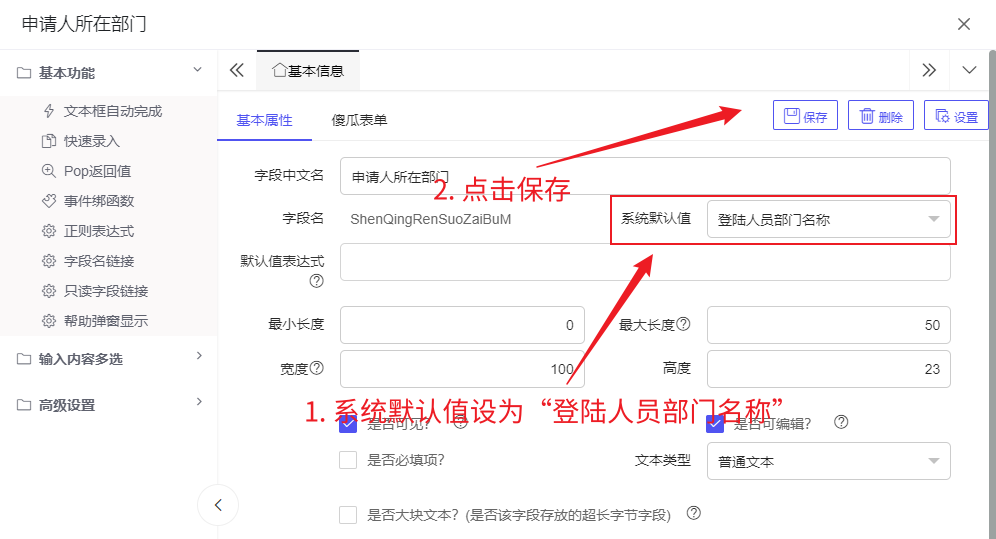
• 申请日期的系统默认值设置为@RDT表示当前日期：

• 设置完成后的表单如下图所示，我们需要将这三个组件设置为只读禁止修改：

• 以申请人姓名组件为例，我们选中这个组件，然后在右侧开启是否只读：

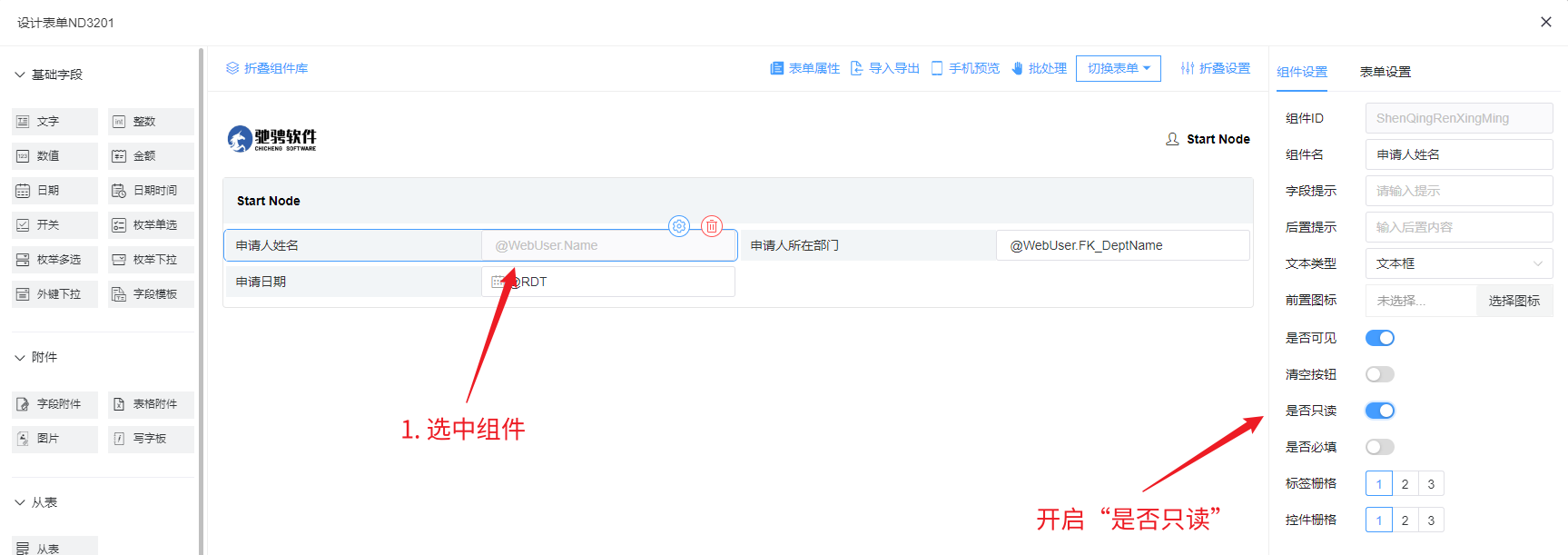
• 申请人所在部门、申请日期的设置只读方式和前面的相同，设置完成后的效果图如下：

2. 接下来，我们再添加两个组件：请假类别、请假事由。

• 请假类别我们使用枚举单选控件，将其拉入表单中，此时会弹出一个添加枚举值字段的窗口，点击新建：

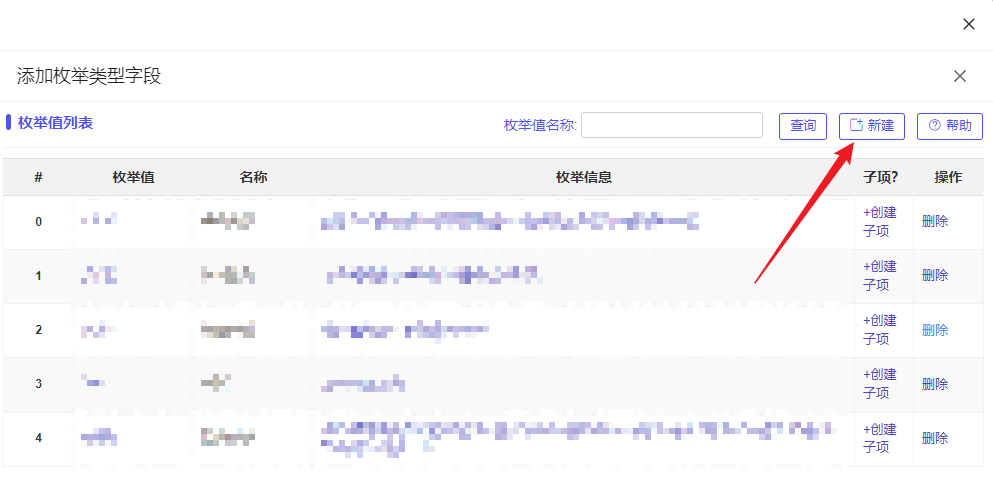
• 标签填写请假类别，对应的类别名称我们填写到下面的枚举框中，完成后点击保存：

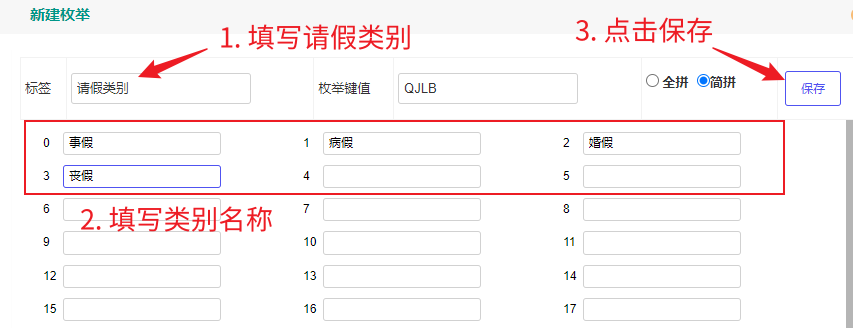
• 选择请假类别的枚举值：

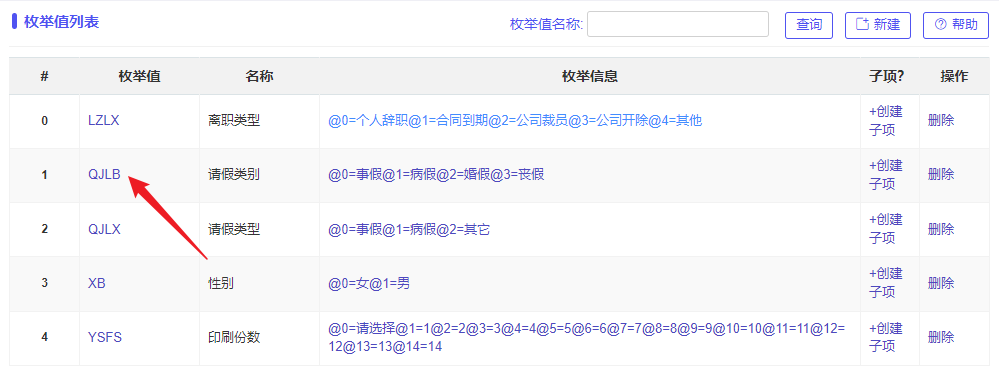
• 弹出框的内容，点击确定：

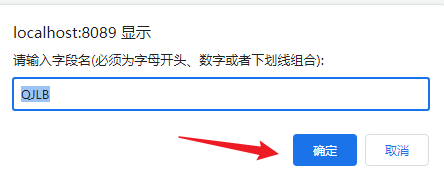
• 点击保存：

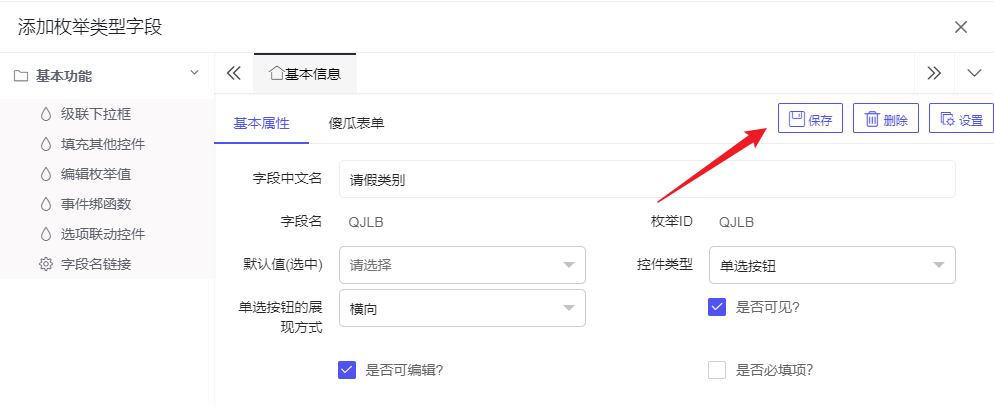
• 选择请假事由组件，在右侧组件设置中的文本类型设置为大块文本，开启超长文本，控件栅格选择整行：

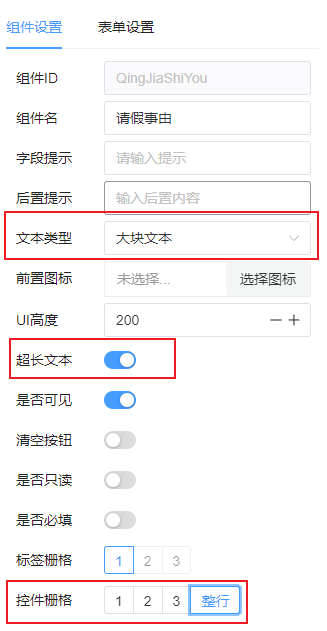
3. 接下来，我们为开始时间、结束时间、请假时长这三个组件设置规则：

• 选中开始时间，点击齿轮，修改组件基本信息：选择日期输入限制，输入日期大于或等于当前日期，设置规则如下图所示：

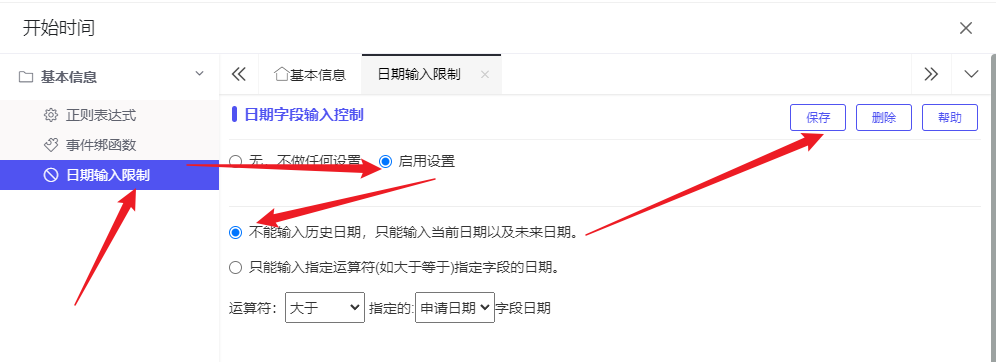
• 选中结束时间，点击齿轮，修改组件基本信息：选择日期输入限制，输入日期大于等于请假开始时间，设置规则如下图所示：

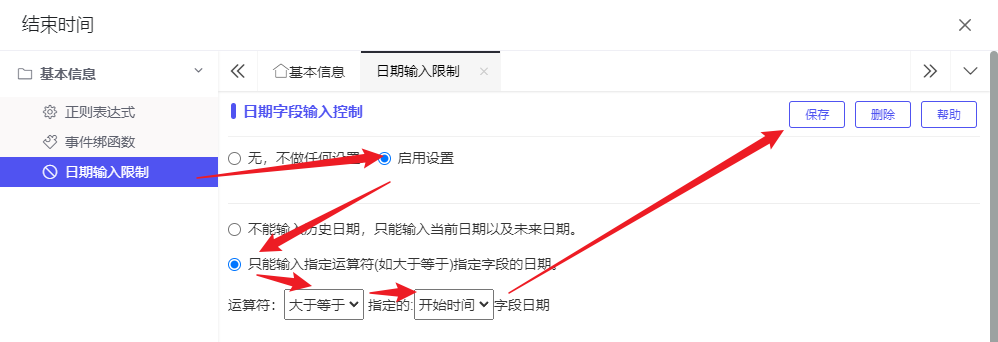
• 选中请假时长，点击齿轮，修改组件基本信息：

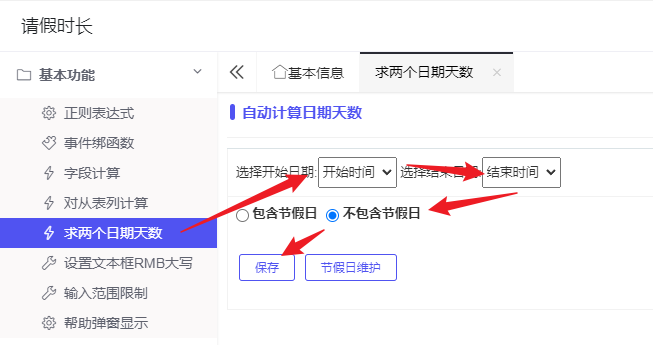
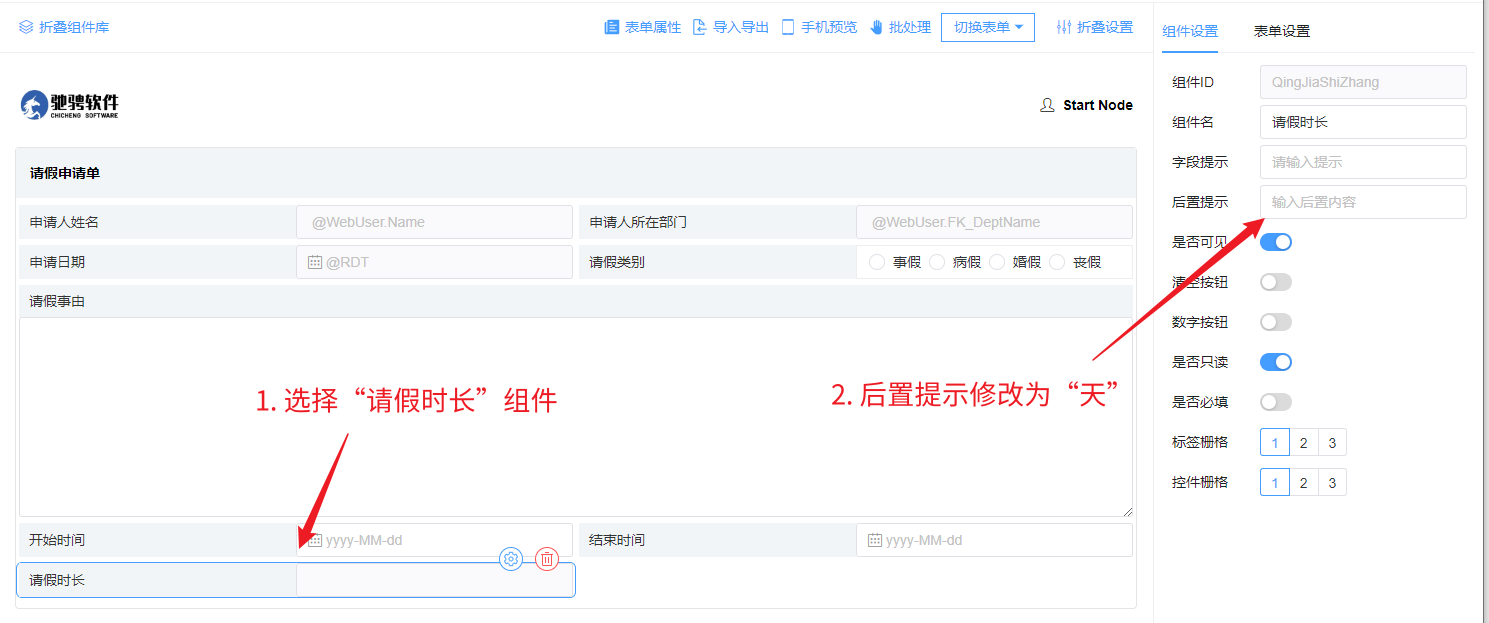
• 为了更好向用户展示请假时长，我们需要对请假时长设置时间单位，由于我们在前面选择的是日期格式，因此请假时长单位是以天为单位：选中组件，在右侧组件设置的后置提示设置为“天”

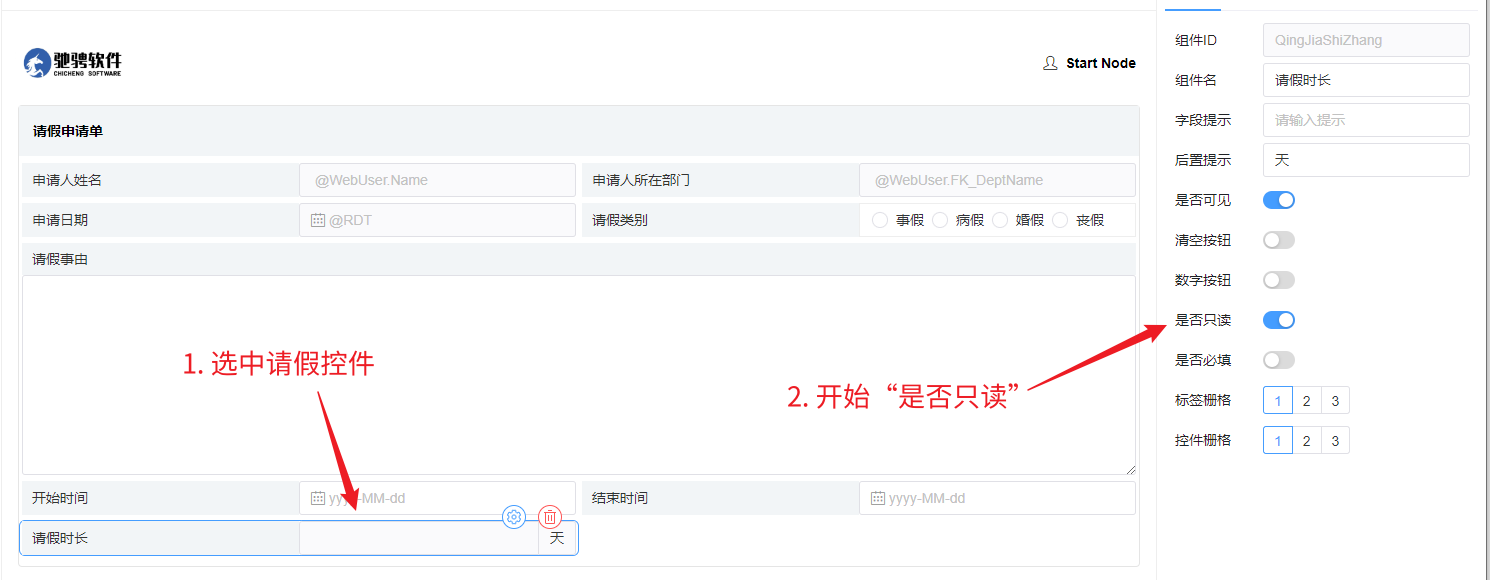
• 请假是由用户填写上述的上述的开始日期和结束日期，经过系统计算而得出的，因此这一部分不需要我们填写，我们把这个控件设置为只读即可：选中请假时长控件，在右侧开启是否只读：

4. 点击最外面的组件，在右侧我们修改一下组件名字为：请假申请单

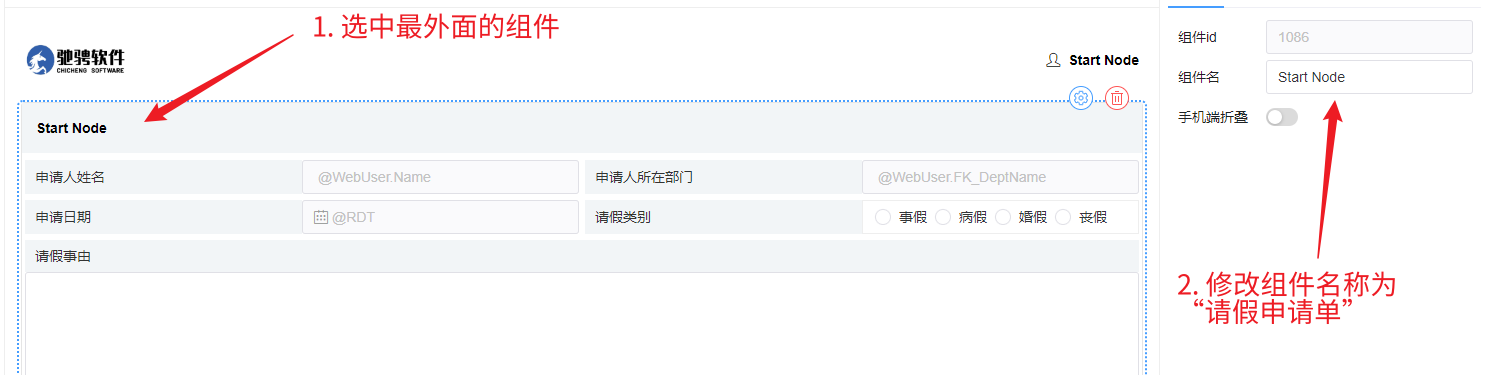
5. 至此，“员工填写请假申请”节点的表单绘制完成，效果图如下图所示：

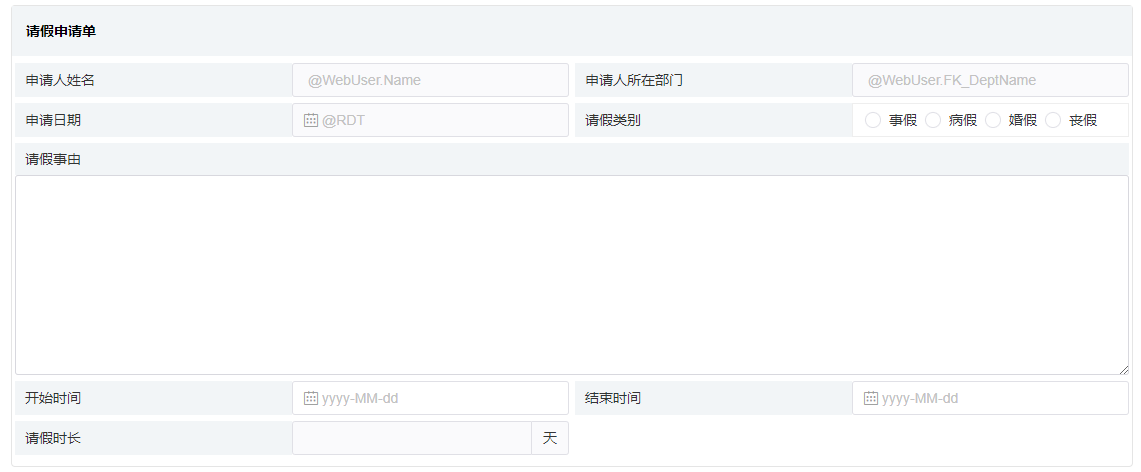
当然，我们只绘制了一个节点表单，那么其他节点的表单也在上述表单的基础上进行绘制。如何在这个表单的基础上绘制其他节点的表单，以及后续所有表单绘制完成后的操作如何，我们放到下一篇文章讲解。