OData – 权限管理

前言

OData 其实没有权限的机制, Client 可以任意的 $select, $expand. 即便它可以做简单防御设置, 但是离平常的业务需求还是很远.

一般上 query entity 常见的需求是, 不能 $select 某些 property, 不能 expand 某些 propety, 需要过滤掉一些 row.

参考:

OData V4 modify $filter on server side

Web API OData Security per Entity

Missing documentation for FilterQueryValidator

解决思路

多 API

传统的方式就是开多几个 API, 然后在 API 上做权限访问.

这个方案不好, OData 的目的就是要减少接口丫.

Query Validator

OData 可以扩展写 $select, $expand 的 validator, 如果 client-side 要求超出范围就报错.

要过滤没有权限访问的数据, 就在 Controller 返回的 IQueryable 上做.

这个方案比较 OData way, 它本身就有 validation query 的概念, 过滤数据本来它就可以不需要负责.

Modify Query in Server-Side

发现 $select, $expand 超出权限就移除, 要过滤没有权限访问的数据就加 $filter.

这个方案比较不 OData way, 它本身没有 server-side 修改 query 的概念. 但是这个方案 client-side 会比较喜欢. 有时候 igrone 会比报错来的简单.

具体实现

Modify Query in Server-Side

OData V4 modify $filter on server side

这一篇给出了 2 个方案,

第 1 个是, override ApplyQuery

查源码会看到

EnableQueryAttribute 是一个 ActionFilterAttribute

实现了 OnActionExecuting 和 OnActionExecuted

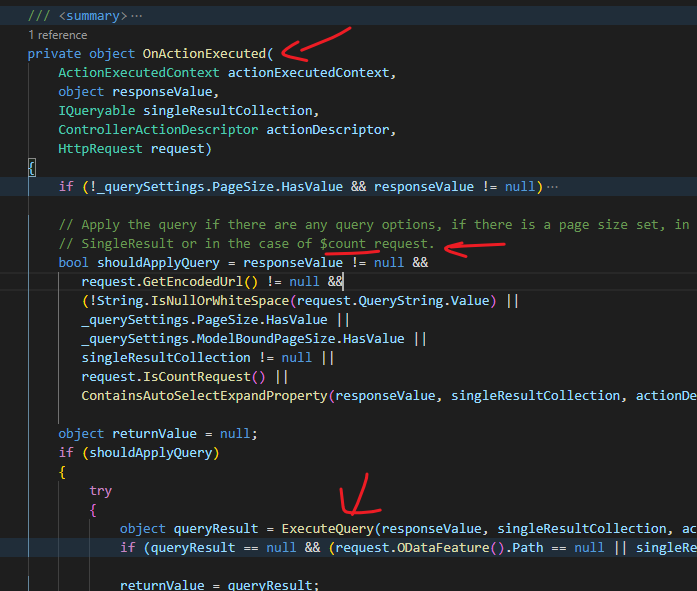
在 OnActionExecuted 它会创建 ODataQueryOptions 然后调用 ApplyQuery

第 1 个方法就是 override 掉这个 ApplyQuery, 在里面偷龙转凤把 request 换掉, 创建新的 ODataQueryOptions 去 apply.

从源码上看, 可以看出 OData 并没有计划让我们去扩展支持这类功能, 属于 hack 的方式来的. 而这个 hack 也很糟糕.

比如如果 request 没有 query 其实是不会进入到 ApplyQuery 的. 所以并不能满足所有的需求. 另外 request 还有用于 $count 这个也在 ApplyQuery 之外, 所以回答里才需要额外的去处理 count 的问题.

第 2 个方法也是属于 hack 的 way 但比第一个好多了.

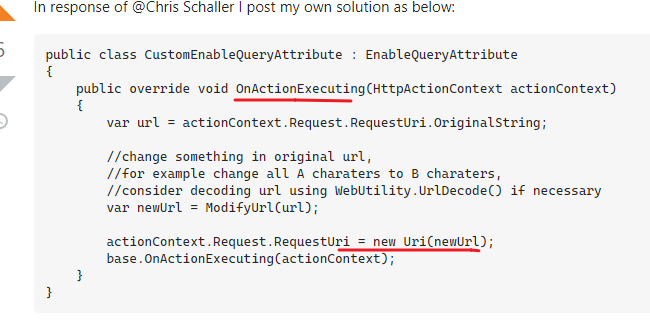
在 OnActionExecuting 直接把 URI 给换了, 那么到 OData 接手时就已经是修改后的 query 了. 省去了许多麻烦. 但无论如何这依然是 hack 的 way 不保证能长期使用.