ETL工具-nifi干货系列 第十三讲 nifi处理器QueryDatabaseTable查询表数据实战教程
1、处理器QueryDatabaseTable,该组件生成一个 SQL 查询,或者使用用户提供的语句,并执行它以获取所有在指定的最大值列中值大于先前所见最大值的行。查询结果将被转换为 Avro 格式,如下图所示:
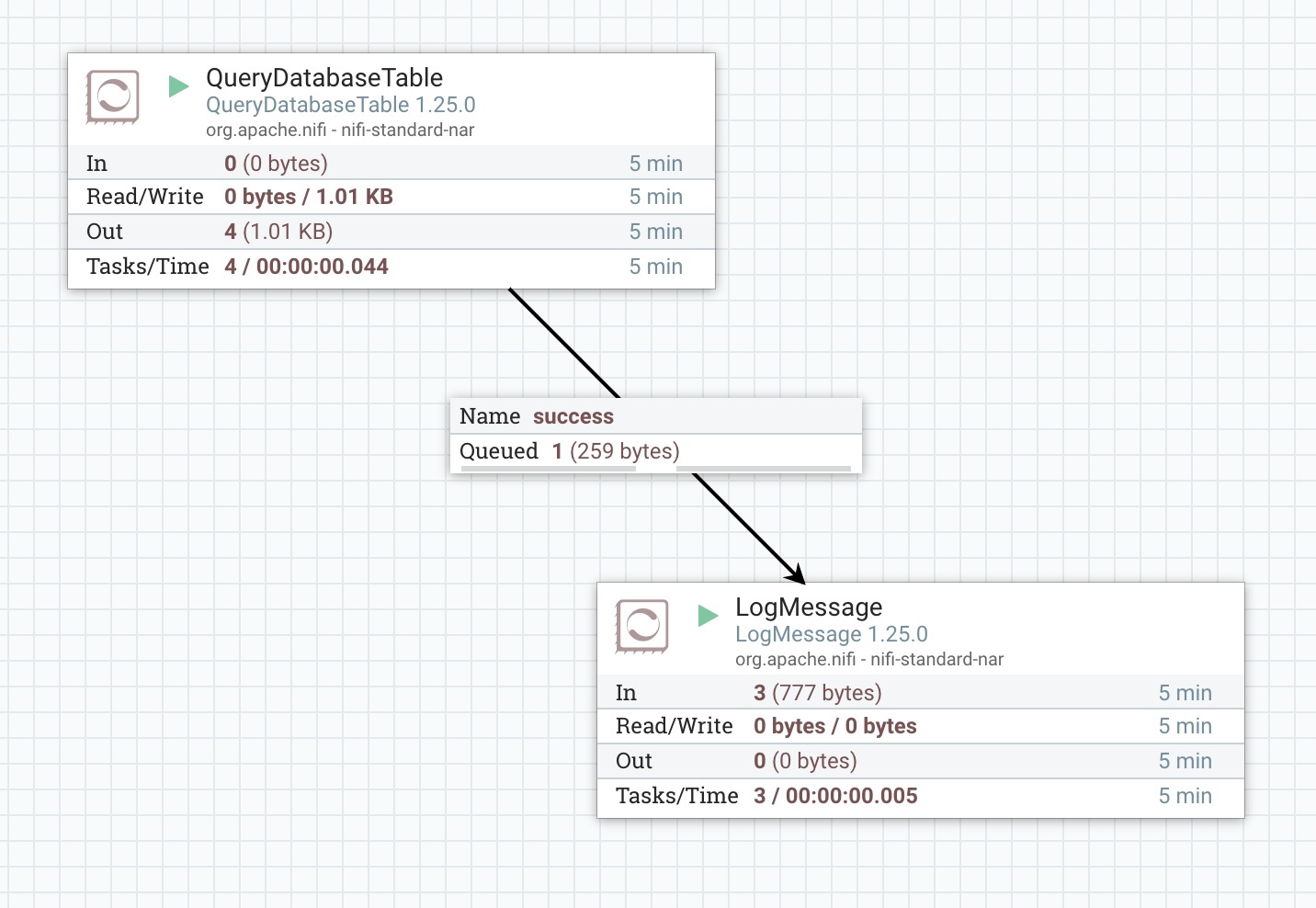
本示例通过QueryDatabaseTable处理器连接数据库查询表数据,然后连接到LogMessage打印日志消息。
2、处理器QueryDatabaseTable属性配置,如下图所示:
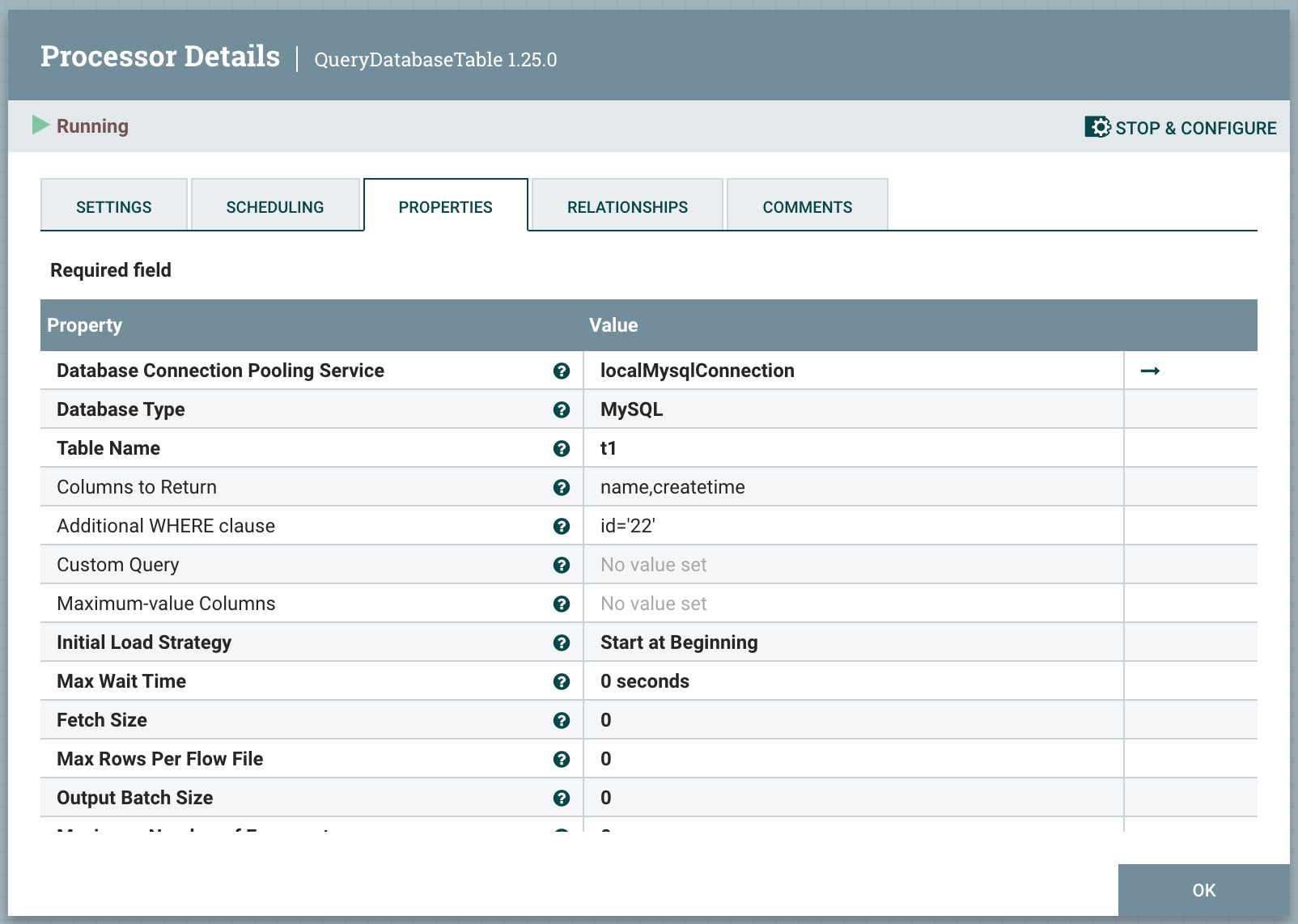
Database Connection Pooling Service:设置数据库连接信息,如设置ip,端口,用户名,密码等。
Database Type:设置数据库类型,有如下选项Generic 、Oracle 、Oracle 12+ 、MS SQL 2012+ 、MS SQL 2008 、MySQL 、PostgreSQL 、Phoenix 。本次演示采用mysql。
Table Name:设置表名,这里设置为t1。
Columns to Return:一个逗号分隔的列名列表,用于在查询中使用。如果您的数据库对这些名称需要特殊处理(例如引号),每个名称都应包括此处理方式。如果未提供列名,则将返回指定表中的所有列。
Additional WHERE clause:构建 SQL 查询时要添加到 WHERE 条件中的自定义子句。
Custom Query:自定义查询语句,如select * from t1 where id='22';
Maximum-value Columns:一个逗号分隔的列名列表。处理器将跟踪自处理器启动以来返回的每个列的最大值。使用多个列意味着对列列表有一个顺序,并且预期每个列的值增长速度比前一个列的值慢。因此,使用多个列意味着列的分层结构,通常用于分区表。此处理器可用于仅检索自上次检索以来已添加/更新的行。请注意,一些 JDBC 类型,如 bit/boolean,并不利于维护最大值,因此不应在此属性中列出这些类型的列,并且在处理过程中会导致错误。如果未提供列,则将考虑来自表的所有行,这可能会影响性能。注意:为了使增量获取正常工作,对于给定表格,使用一致的最大值列名非常重要。
Initial Load Strategy:
Max Wait Time:运行中的 SQL 查询所允许的最长时间,零表示没有限制。小于1秒的最长时间将等同于零。
Fetch Size:每次从结果集中获取的结果行数。这是对数据库驱动程序的提示,可能不会被采纳和/或精确执行。如果指定的值为零,则提示将被忽略。
Max Rows Per Flow File:单个FlowFile中将包含的最大结果行数。这将允许您将非常大的结果集分成多个FlowFiles。如果指定的值为零,则所有行都将在单个FlowFile中返回。
Output Batch Size:在提交处理会话之前排队的输出FlowFiles的数量。当设置为零时,会话将在所有结果集行都已处理并且输出FlowFiles准备好传输到下游关系时提交。对于大型结果集,这可能会导致在处理器执行结束时传输大量的FlowFiles。如果设置了此属性,则当指定数量的FlowFiles准备好传输时,会话将被提交,从而释放FlowFiles到下游关系。注意:当设置此属性时,FlowFiles上将不设置maxvalue.*和fragment.count属性。
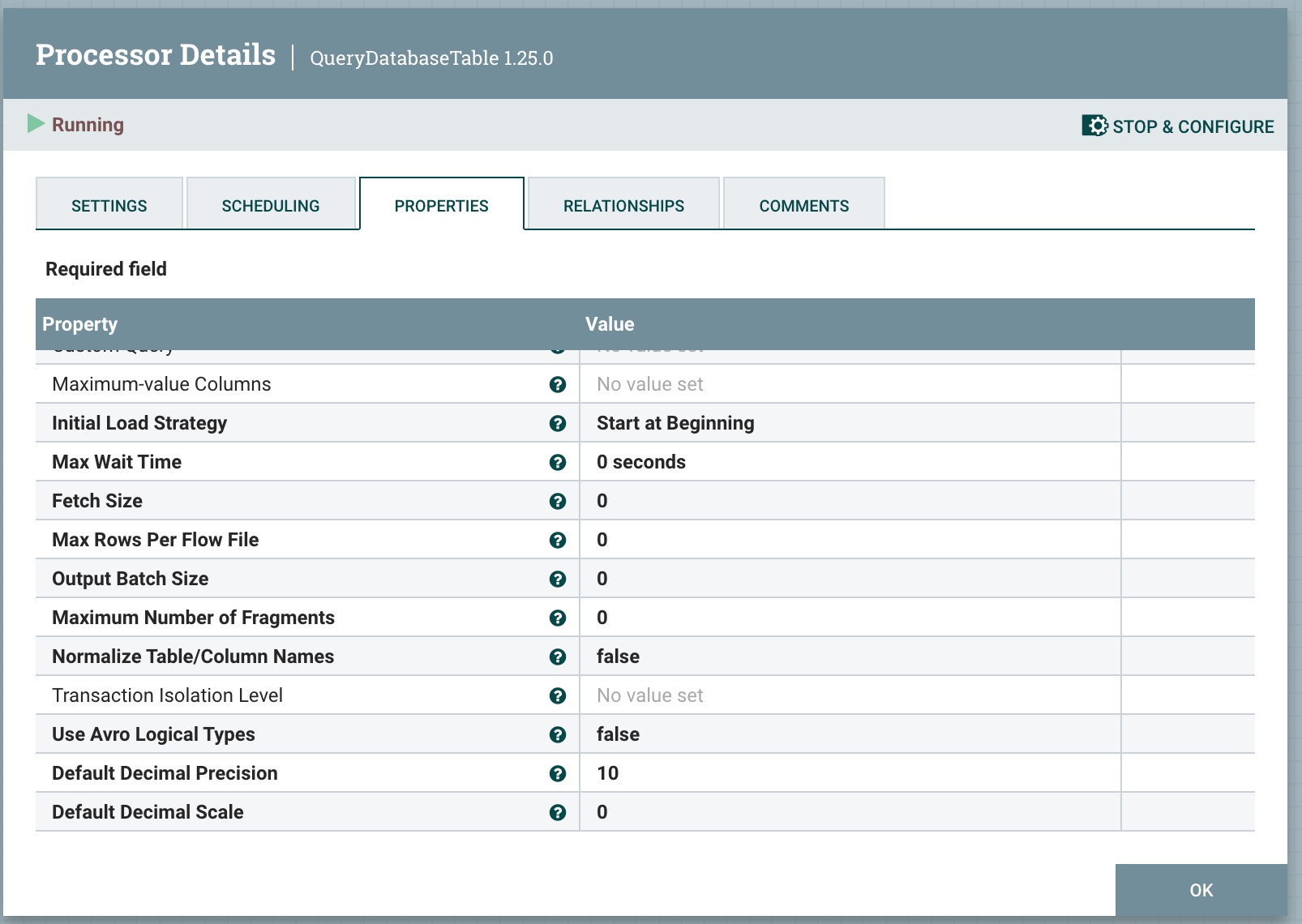
Maximum Number of Fragments:最大碎片数量。如果指定的值为零,则返回所有碎片。当此处理器摄取大型表格时,这可以防止OutOfMemoryError。注意:设置此属性可能会导致数据丢失,因为传入的结果未排序,并且碎片可能在不包含在结果集中的行的任意边界结束。
Normalize Table/Column Names:是否将列名中的非Avro兼容字符更改为Avro兼容字符。例如,冒号和句点将被更改为下划线,以构建有效的Avro记录,有true和false两个选项。
Transaction Isolation Level:此设置将为支持此设置的驱动程序设置数据库连接的事务隔离级别。
Use Avro Logical Types:是否使用 Avro 逻辑类型来处理 DECIMAL/NUMBER、DATE、TIME 和 TIMESTAMP 列。如果禁用,则写入为字符串。如果启用,则使用逻辑类型并按其底层类型写入,具体来说,DECIMAL/NUMBER 作为逻辑 ‘decimal’:按字节写入,并附加精度和比例元数据,DATE 作为逻辑 ‘date-millis’:按整数写入,表示自 Unix 纪元(1970-01-01)以来的天数,TIME 作为逻辑 ‘time-millis’:按整数写入,表示自 Unix 纪元以来的毫秒数,以及 TIMESTAMP 作为逻辑 ‘timestamp-millis’:按长整数写入,表示自 Unix 纪元以来的毫秒数。如果写入的 Avro 记录的读取器也了解这些逻辑类型,那么根据读取器实现的不同上下文,这些值可以以更多的上下文进行反序列化。
Default Decimal Precision:当 DECIMAL/NUMBER 值被写入为 ‘decimal’ Avro 逻辑类型时,需要指定表示可用数字的数量的特定 ‘precision’。通常,精度由列数据类型定义或数据库引擎默认值定义。然而,一些数据库引擎可能会返回未定义的精度(0)。在写入这些未定义精度的数字时,将使用“默认十进制精度”。
Default Decimal Scale:当 DECIMAL/NUMBER 值被写入为 ‘decimal’ Avro 逻辑类型时,需要指定表示可用小数位数的特定 ‘scale’。通常,scale 由列数据类型定义或数据库引擎默认值定义。然而,当返回未定义的精度(0)时,在某些数据库引擎中,scale 也可能不确定。在写入这些未定义数字时,将使用“默认十进制 scale”。如果一个值的小数位数超过指定的 scale,则该值将四舍五入,例如,scale 为 0 时,1.53 变为 2,scale 为 1 时,1.5。
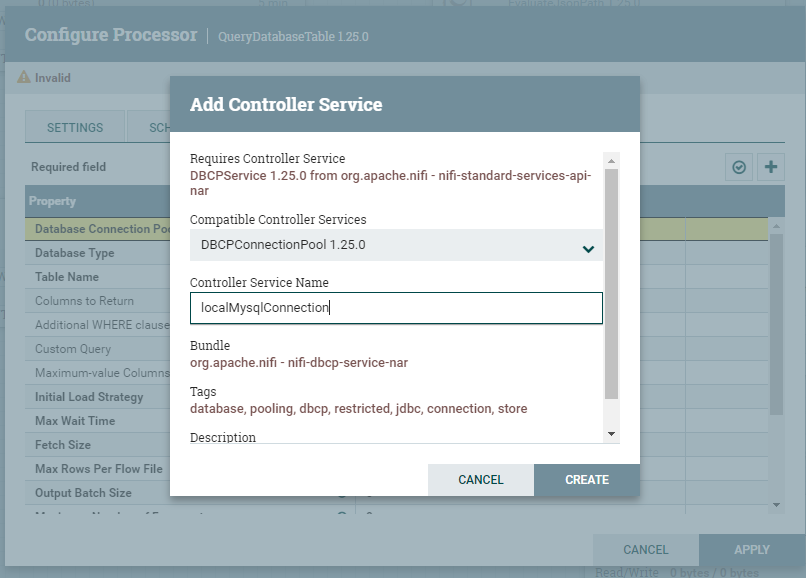
3、控制器服务,配置数据库连接,点击Database Connection Pooling Service 属性对应的值,选择Create new service,如下图所示:
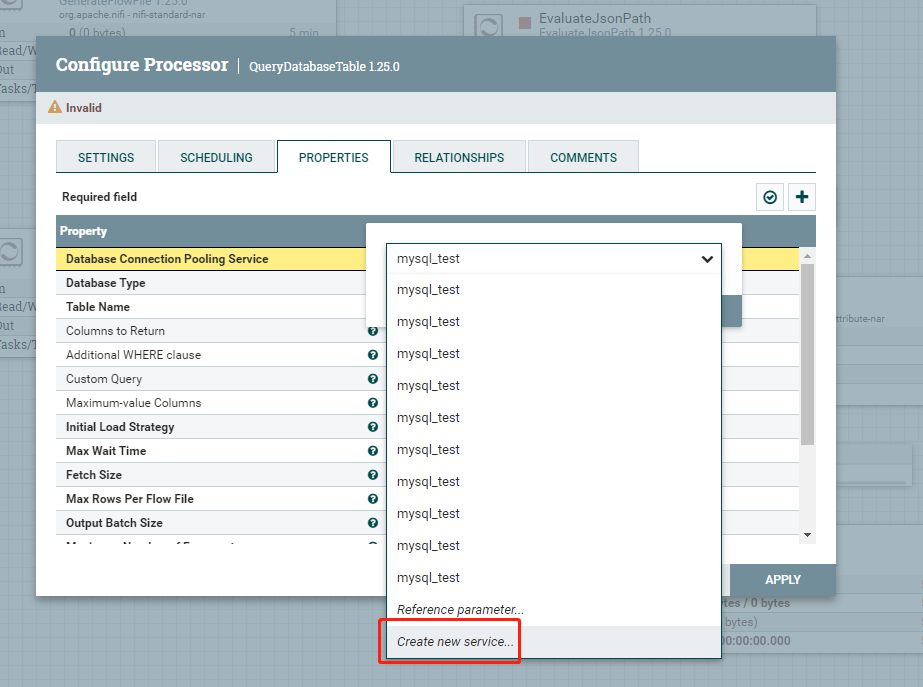
选择合适的Compatible Controller Services,自定义Controller Service Name,如下图所示。
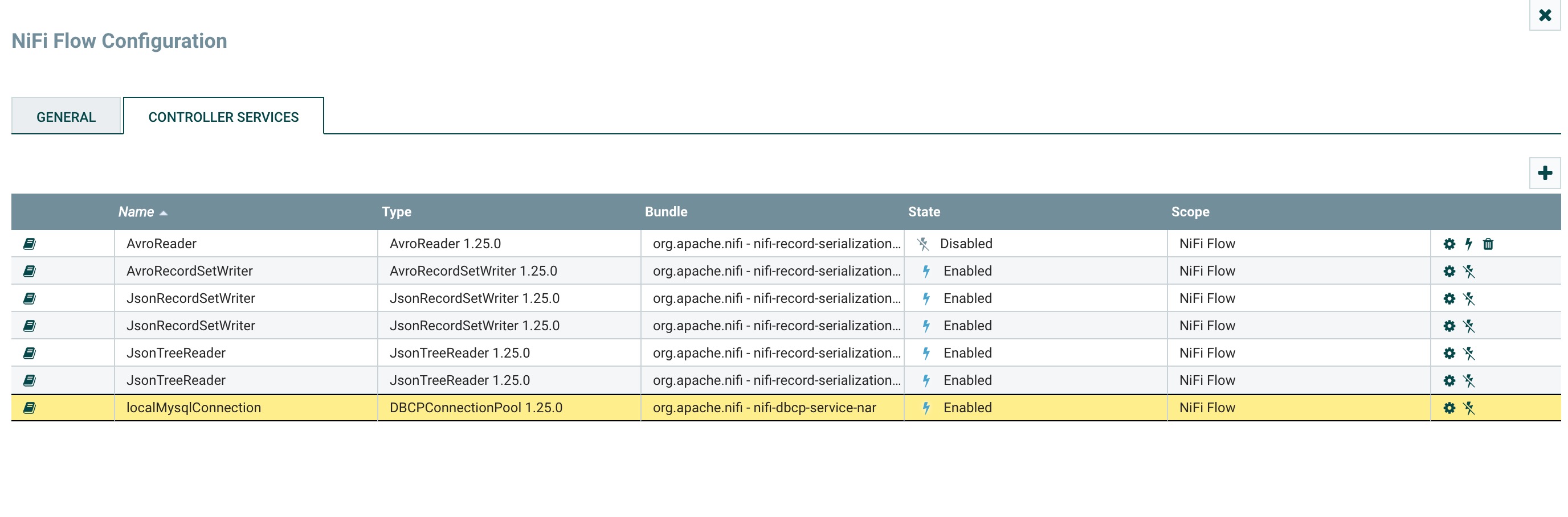
下种中的齿轮可以进行设置数据库连接信息,闪电标记可以启用和禁用。
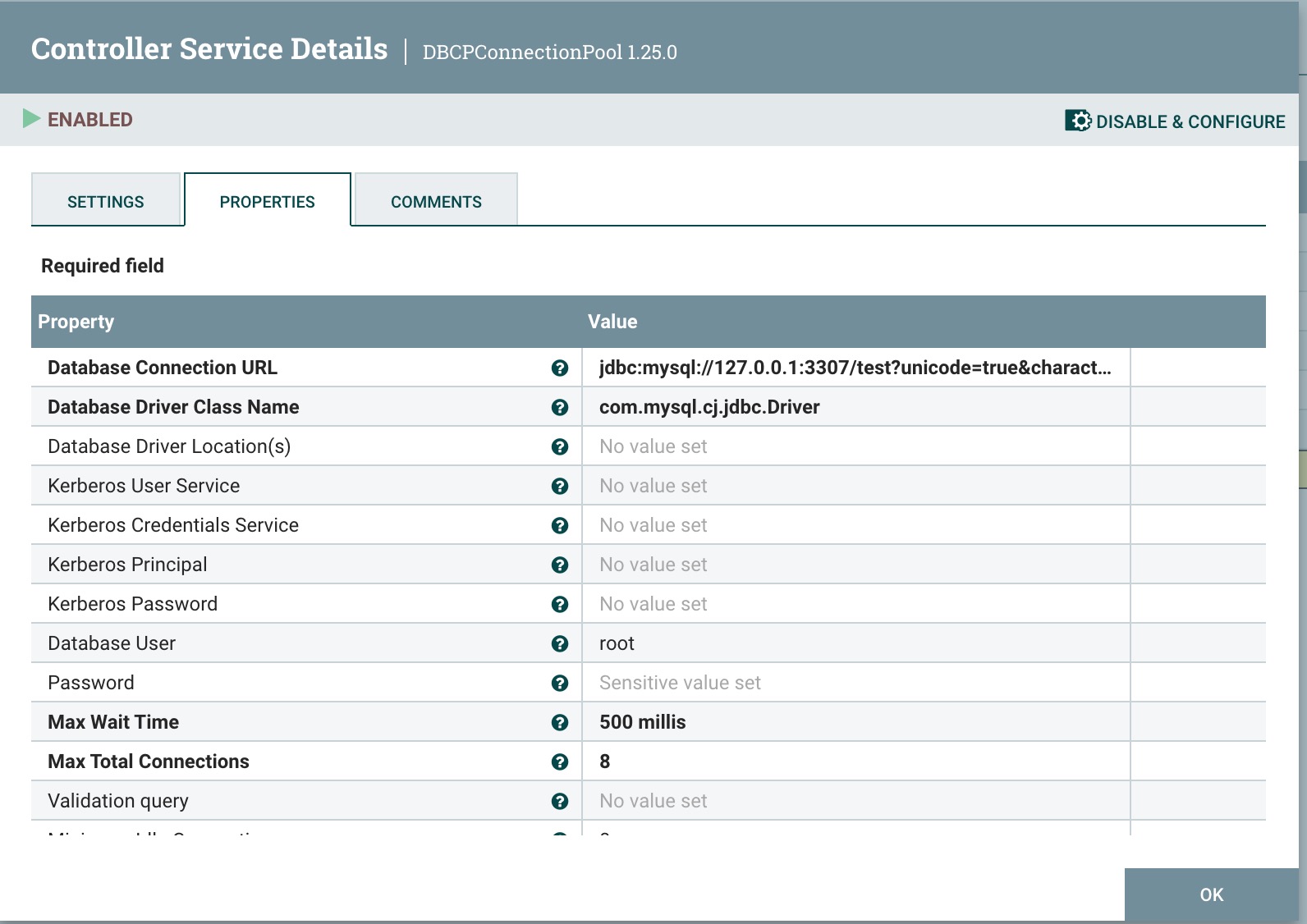
点击齿轮进行配置数据库连接信息,填写主要信息Database Connection Url、Database Driver Class Name,Database user和Password,如下图所示:
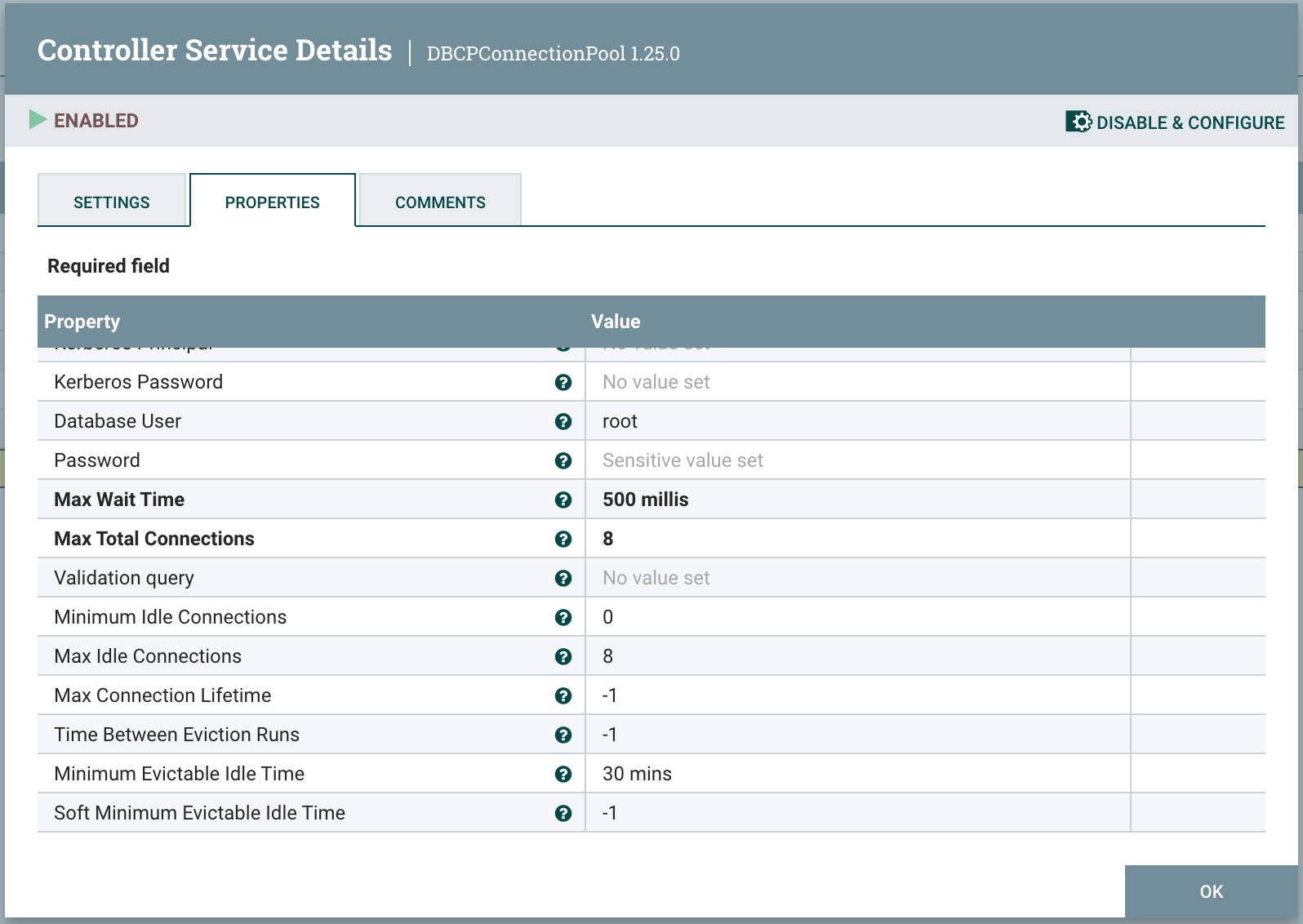
4、点击运行,然后查看数据溯源信息,attributes 中多了tablename、querydbtable.row.count、mime.type属性如下图所示:
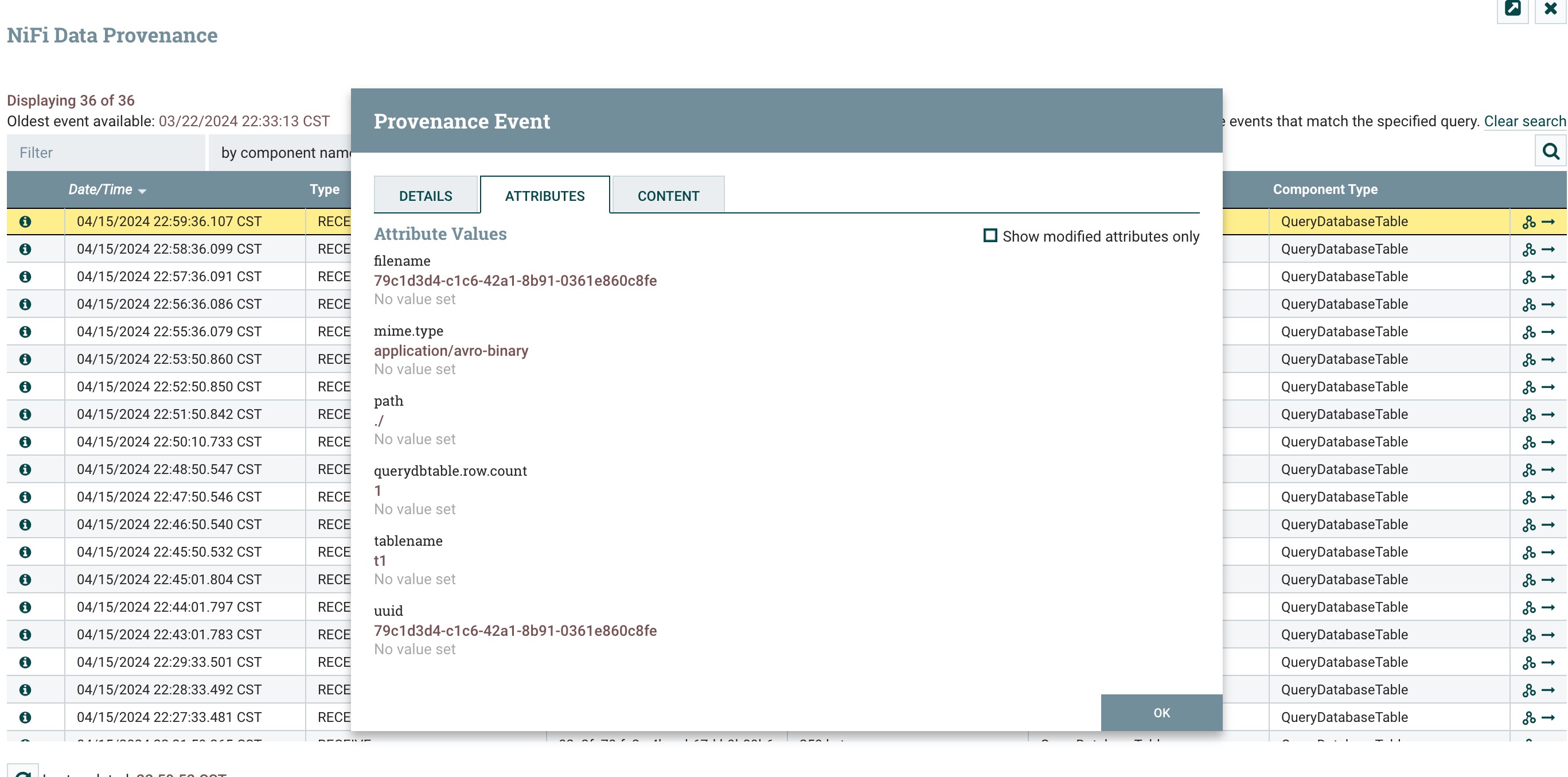
点击content选项卡,可以看到flowfile的content,点击view进行查看数据,如下图所示:
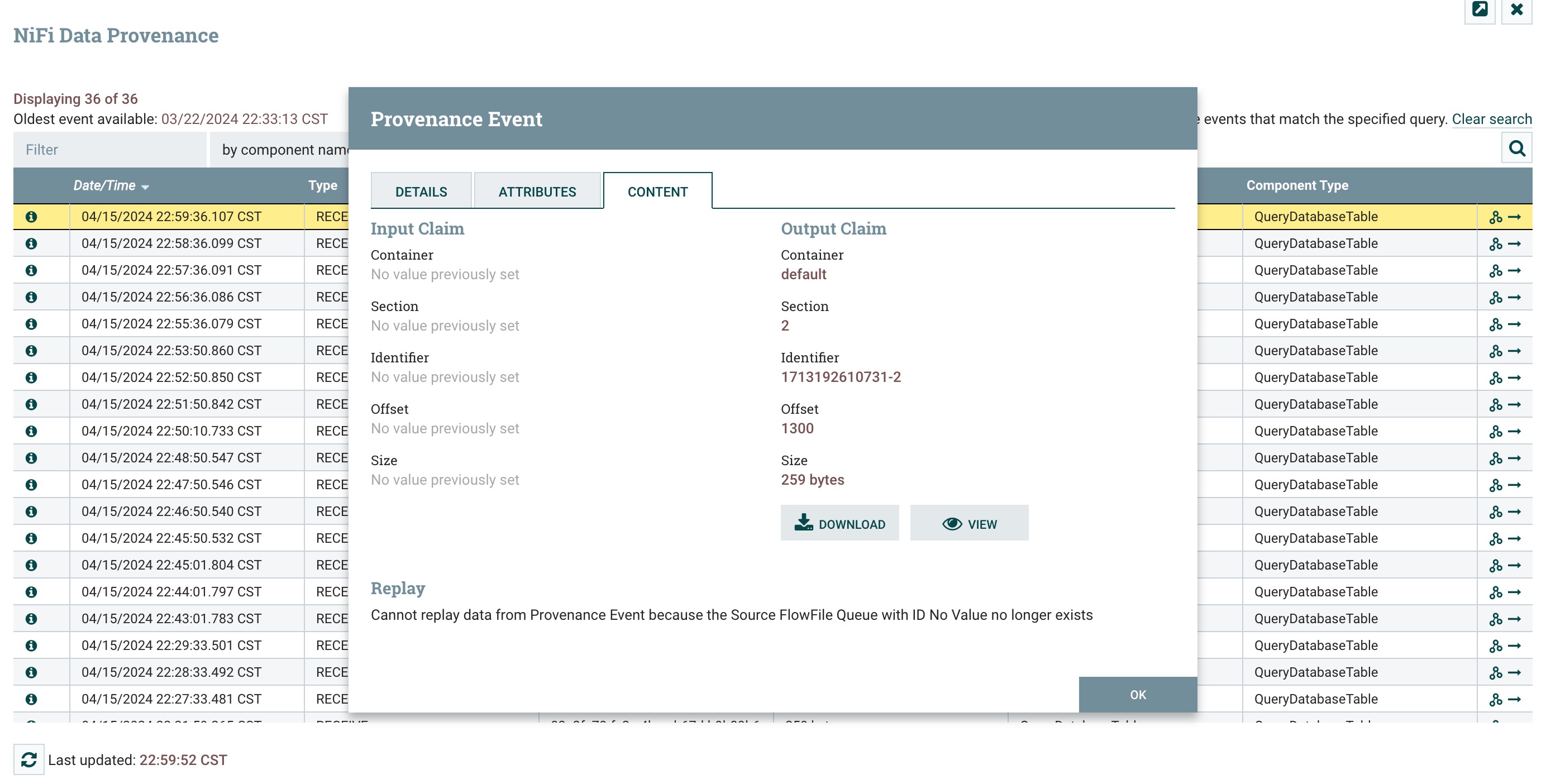
点击view查看数据,默认orginal格式为avro二进制数据所以会有中文乱码的情况,此处乱码不影响,忽略即可,如下图所示:
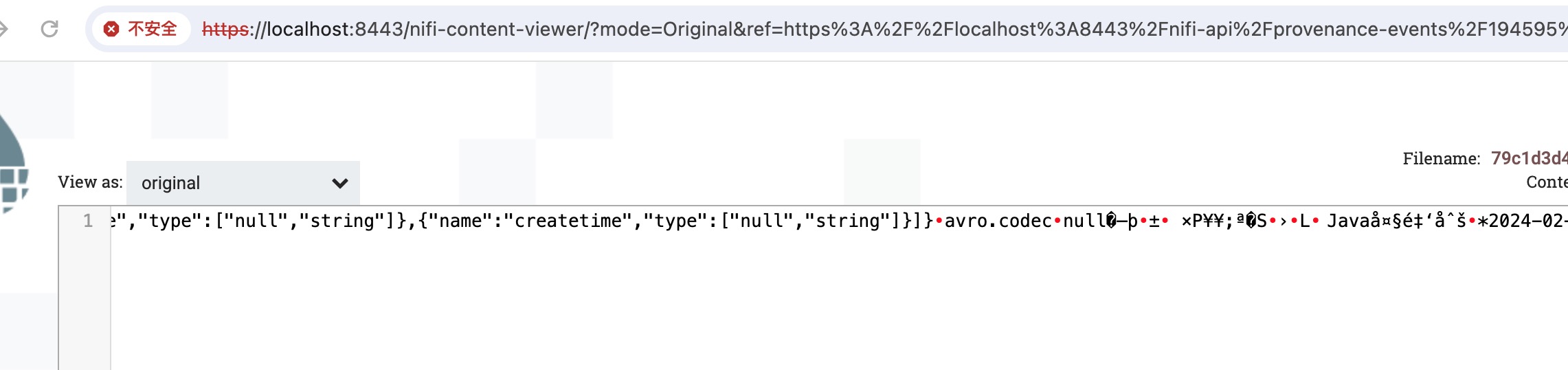
选择formatted,输出json格式的数据,如下图所示:
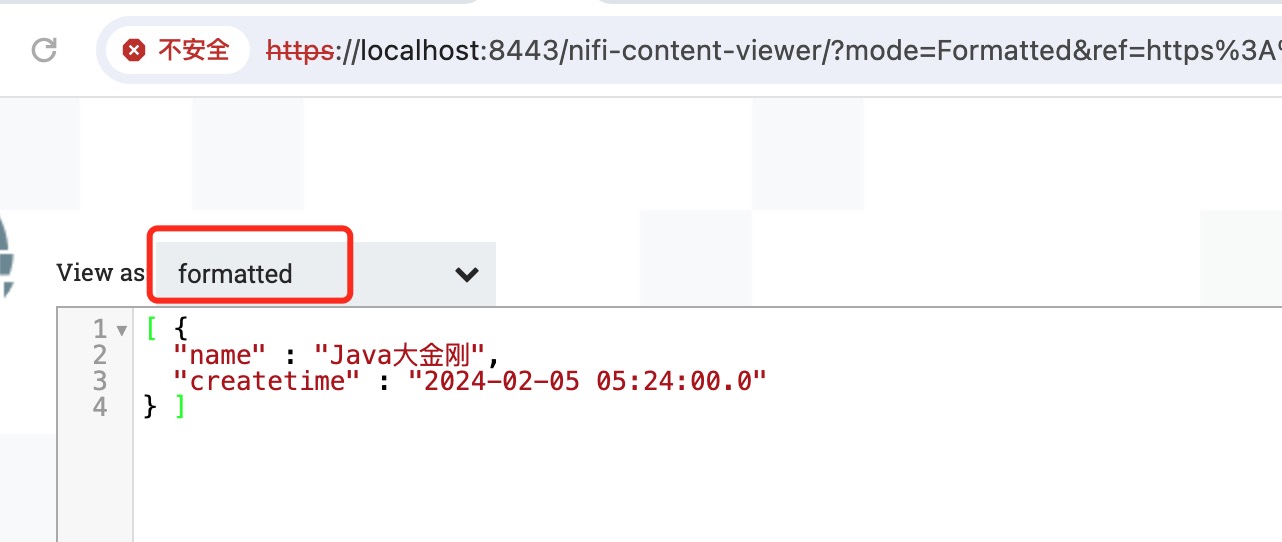

ETL工具-nifi干货系列 第十三讲 nifi处理器QueryDatabaseTable查询表数据实战教程的更多相关文章
- ETL工具之Kettle的简单使用一(不同数据库之间的数据抽取-转换-加载)
ETL工具之Kettle将一个数据库中的数据提取到另外一个数据库中: 1.打开ETL文件夹,双击Spoon.bat启动Kettle 2.资源库选择,诺无则选择取消 3.选择关闭 4.新建一个转换 5. ...
- Selenium系列(十四) - Web UI 自动化基础实战(1)
如果你还想从头学起Selenium,可以看看这个系列的文章哦! https://www.cnblogs.com/poloyy/category/1680176.html 其次,如果你不懂前端基础知识, ...
- Selenium系列(十五) - Web UI 自动化基础实战(2)
如果你还想从头学起Selenium,可以看看这个系列的文章哦! https://www.cnblogs.com/poloyy/category/1680176.html 其次,如果你不懂前端基础知识, ...
- Selenium系列(十六) - Web UI 自动化基础实战(3)
如果你还想从头学起Selenium,可以看看这个系列的文章哦! https://www.cnblogs.com/poloyy/category/1680176.html 其次,如果你不懂前端基础知识, ...
- Selenium系列(十八) - Web UI 自动化基础实战(5)
如果你还想从头学起Selenium,可以看看这个系列的文章哦! https://www.cnblogs.com/poloyy/category/1680176.html 其次,如果你不懂前端基础知识, ...
- Selenium系列(十九) - Web UI 自动化基础实战(6)
如果你还想从头学起Selenium,可以看看这个系列的文章哦! https://www.cnblogs.com/poloyy/category/1680176.html 其次,如果你不懂前端基础知识, ...
- etl学习系列1——etl工具安装
ETL(Extract-Transform-Load的缩写,即数据抽取.转换.装载的过程),对于企业或行业应用来说,我们经常会遇到各种数据的处理,转换,迁移,所以了解并掌握一种etl工具的使用,必不可 ...
- 集团公司(嵌入ETL工具)财务报表系统解决方案
集团公司(嵌入ETL工具)财务报表系统解决方案 一.项目背景: 某集团公司是一家拥有100多家子公司的大型集团公司,旗下子公司涉及各行各业,包括:金矿.铜矿.房产.化纤等.由于子公司在业务上的差异,子 ...
- 系统设计与架构笔记:ETL工具开发和设计的建议
最近项目组里想做一个ETL数据抽取工具,这是一个研发项目,但是感觉公司并不是特别重视,不重视不是代表它不重要,而是可能不会对这个项目要求太高,能满足我们公司的小需求就行,想从这个项目里衍生出更多的东西 ...
- Neo4j ETL工具快速上手:简化从关系数据库到图数据库的数据迁移
注:本文系从https://medium.com/neo4j/tap-into-hidden-connections-translating-your-relational-data-to-graph ...
随机推荐
- whistle代理使用
1. 介绍 whistle(读音[ˈwɪsəl],拼音[wēisǒu])基于Node实现的跨平台web调试代理工具,类似的工具有Windows平台上的Fiddler,主要用于查看.修改HTTP.HTT ...
- 第六課-Channel Study For TCP Listener & HTTP Listener & Web Service Listener About Response Handler
经过前面章节的课程,对Mirth Connect在系统集成与数据交互中的使用有了一个大概的了解:大家一定有个疑惑,Mirth Connect如何组织响应消息并返回给调用者?今天我们就来继续深入讲解Re ...
- Arthas 初探--安装初步适用
简介: 由于在项目中遇到一种情况,某段代码在进行单元测试和在 tomcat 容器中运行的性能相差数百倍,因此需要分析在不同环境下某个方法执行的具体时间,从而确定问题.Arthas 可以做到无侵入的监控 ...
- 5月25日,阿里云开源 PolarDB-X 将迎来重磅升级发布
简介:2022年5月25日,阿里云开源 PolarDB-X 将升级发布新版本!PolarDB-X 从 2009 年开始服务于阿里巴巴电商核心系统, 2015 年开始对外提供商业化服务,并于 2021 ...
- 走近Quick Audience,了解消费者运营产品的发展和演变
简介: Quick Audience产品是一款云原生面向消费者的营销产品,自诞生以来,经历了三个发展阶段.每个阶段的转变,都与互联网环境和消费者行为的变迁有着极大的关联. Quick Audien ...
- [FAQ] crontab 执行curl xxx 好像没有执行 ?
如果你的crontab任务中的curl命令没有执行,可能有几个原因需要检查: 1. 检查命令路径:确保你在crontab任务中指定了正确的curl命令路径.你可以使用 which curl 命令来 ...
- [Trading] 专业交易: 专业交易员和散户交易员的不同, 什么是专业交易员
专业交易员可能用的是公司的钱或者自己的钱 有基本工资支持,散户用的是自己的钱 没有人提供工资来做交易. 目标不同,专业交易员的目的是增长投资账户和获得奖金,散户大部分是为了提取盈利收入而无法增长投资账 ...
- [Ethereum] 浅谈 ERC20 在 openzeppelin-contracts 中的结构与实现
目前 openzeppelin-contracts 的稳定版是 v2.5,截止到本文发布,最新的 Tag 为 v3.0.0-rc.0 以下是 token/ETC20 的文件列表: IERC20.sol ...
- dotnet 8 WPF 支持在 RDP 远程桌面状态下启用渲染硬件加速
本文将和大家介绍在 dotnet 8 里 WPF 引入的新功能之一,在 RDP 远程桌面状态下启用渲染硬件加速 在 dotnet 8 之前,在用户进行 RDP 远程桌面时 WPF 应用将默认关闭硬件渲 ...
- dotnet CBB 为什么决定推送 Tag 才能打包
通过推送 Tag 才打 NuGet 包的方法的作用不仅仅是让打包方便,让打包这个动作可以完全在本地执行,无需关注其他系统的使用步骤.更重要的是可以强制每个可能被安装的 NuGet 包版本都能有一个和他 ...
