线性dp：最长公共子序列

最长公共子序列

• 本文讲解的题与leetcode1143.最长公共子序列这题一样，阅读完可以挑战一下。

力扣题目链接

题目叙述：

给定两个字符串，输出其最长公共子序列，并输出它的长度

输入：

ADABEC和DBDCA

输出：

DBC
3

解释

最长公共子序列是DBC，其长度为3

动态规划思路：

• 我们这题先构建一个模型，我们使用两个指针i,j ，分别用于遍历a字符串，b字符串。如图所示：

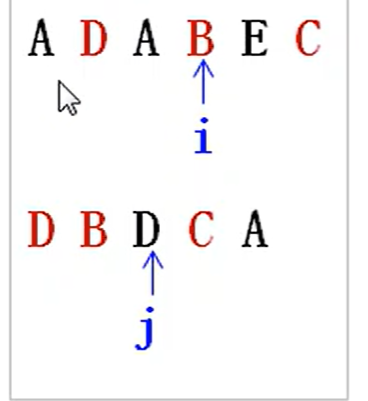
• 然后我们可以设想一个状态变量，也就是一个函数。一个关于两个变量相关的函数，这在代码中体现为二维数组f。

• 然后f[i][j]表示什么呢？表示序列a[1,2,3....i]和b[1,2,3....j]的最长公共子序列的长度

状态变量的含义

• 在这里的状态变量为f[i][j]，它的含义是a的前i个字符与b的前j个字符的最长公共子序列的长度

• 现在就要观察a[i],b[j]是否在当前的最长公共子序列当中。

• 具体情况如下图：

递推公式：

• f[i][j]可以分为三种情况讨论，就是：

1. a[i]，b[j]都在最长公共子序列当中，也就是a[i]==b[j]
2. a[i]!=b[j]，并且a[i]不在公共子序列当中。
3. a[i]!=b[j]，并且b[j]不在公共子序列当中。

• 那我们的递推公式就可与分为两种情况：
  • f[i][j]=f[i-1][j-1]+1 （a[i]==b[j]）
  • f[i][j]=max(f[i-1][j],f[i][j-1]) （a[i]!=b[j]）
• 显而易见，我们的边界条件为：
  • f[0][j]=0
  • f[i][0]=0

//m是a字符串的长度，n是b字符串的长度
for(int i=1;i<=m;i++){
    for(int j=1;j<=n;j++){
        //因为我们的f数组是从下标1开始，而字符串是从0开始的下标
        if(a[i-1]==b[j-1]) f[i][j]=f[i-1][j-1]+1;
        else f[i][j]=max(f[i-1][j],f[i][j-1]);
    }
}

遍历顺序

• 经过上面的分析，明显遍历顺序为i从小到大，j也是从小到大 。

初始化

• 初始化边界为0即可

举例打印dp数组

• 如图所示

如何找出对应的最长公共子序列的长度

• 我们使用p数组来记录每一次f[i][j]的值来源于哪一个方向

  • 1方向代表左上方
  • 2方向代表左方
  • 3方向代表上方

• 代码改造如下：

for(int i=1;i<=m;i++){
    for(int j=1;j<=n;j++){
        if(a[i-1]==b[j-1]){
            f[i][j]=f[i-1][j-1]+1;
            //左上方
            p[i][j]=1;
        }
        else if(f[i-1][j]>f[i][j-1]){
            f[i][j]=f[i][j-1];
   			//左边
            p[i][j]=2;
        }
        else{
            f[i][j]=f[i-1][j];
			//上边
            p[i][j]=3;
        }
    }
}

• p[i][j]代表前驱的位置。

算法的执行过程

• 我们要找到最长公共子序列，只需要找到从结尾开始，往前找到p[i][j]==1，也就是来源于左上方的哪些元素的集合，就是我们的最长公共子序列。（并不是棋盘中所有p[i][j]==1）的元素，而是从右下角出发，往回找到的所有p[i][j]==1的那些元素。
• 例子如下：

• 我们使用s数组来储存最长公共子序列

• 代码实现：

int i,j,k;
char s[200];
i=m;j=n;k=f[m][n];
while(i>0&&j>0){
    //左上方
    if(p[i][j]==1){
        s[k--]=a[i-1];
        i--;j--;
    }
    //左边
    else if(p[i][j]==2) j--;
    //上边
    else i--;
}
for(int i=1;i<=f[m][n];i++) cout<<s[i];

最终代码实现：

#include <iostream>
#include <cstring>
using namespace std;

char a[200];
char b[200];
int f[205][205];
int p[205][205];
int m, n;

void LCS() {
	int i, j;
	m = strlen(a);
	n = strlen(b);

	for (i = 1; i <= m; i++) {
		for (j = 1; j <= n; j++) {
			if (a[i - 1] == b[j - 1]) {
				f[i][j] = f[i - 1][j - 1] + 1;
				p[i][j] = 1;
			}
			else if (f[i - 1][j] > f[i][j - 1]) {
				f[i][j] = f[i - 1][j];
				p[i][j] = 2;
			}
			else {
				f[i][j] = f[i][j - 1];
				p[i][j] = 3;
			}
		}
	}
	cout << f[m][n] << endl;
}
//寻找出当初的最长公共子序列。
void getLCS() {
	int i = m, j = n, k = f[m][n];
	char s[200];
	s[k] = '\0';
	while (i > 0 && j > 0) {
		if (p[i][j] == 1) {
			s[--k] = a[i - 1];
			i--; j--;
		}
		else if (p[i][j] == 2) {
			i--;
		}
		else {
			j--;
		}
	}

	cout << s << endl;
}

int main() {
	cin >> a >> b;
	LCS();
	getLCS();
	return 0;
}