力扣231(java)-2的幂（简单）

题目：

给你一个整数 n，请你判断该整数是否是 2 的幂次方。如果是，返回 true ；否则，返回 false 。

如果存在一个整数 x 使得 n == 2x ，则认为 n 是 2 的幂次方。

示例 1：

输入：n = 1
输出：true
解释：20 = 1
示例 2：

输入：n = 16
输出：true
解释：24 = 16
示例 3：

输入：n = 3
输出：false
示例 4：

输入：n = 4
输出：true
示例 5：

输入：n = 5
输出：false

提示：

-231 <= n <= 231 - 1

进阶：你能够不使用循环/递归解决此问题吗？

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/power-of-two
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解题思路：

一、常规解法

1.如果n的值 <= 0,肯定不为2的幂次方，直接返回false;

2.2的幂次方肯定为偶数，在偶数的前提下，一直对n除2，如果是2的幂次方，最终的 n=1,否则 n = 0。

例如：

n = 12 :    12 / 2 = 6, 6 / 2 = 3, 3 / 2 = 1, 1 / 2 = 0 结束n =0;

n= 16:      16 / 2 = 8, 8 / 2 = 4, 4 / 2 = 2, 2 / 2 = 1 结束 n =1

代码：

 1 class Solution {
 2     public boolean isPowerOfTwo(int n) {
 3         if(n <= 0) return false;
 4         //偶数的前提下
 5         while(n % 2 == 0){
 6             n /= 2;
 7         }
 8         //如果只是偶数而非幂次方，n就会为0
 9         return n == 1;
10     }
11 }

二、二进制位运算

看评论区的大佬，我自己没想到这种~

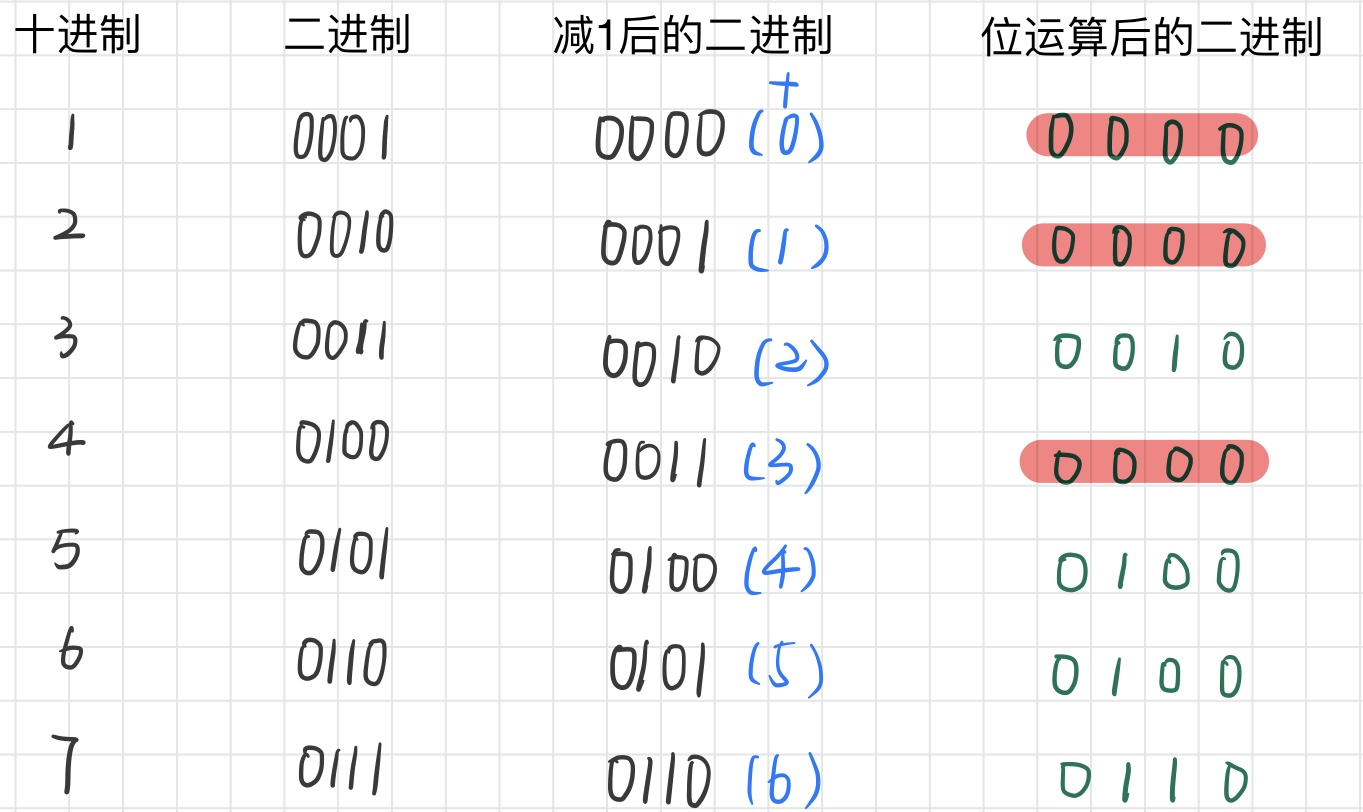
1.n <= 0是肯定不会为2的幂次方的；

2. n > 0的情况下，如果n是2的幂次方，则一定满足 n & (n-1) == 0

代码：

1 class Solution {
2     public boolean isPowerOfTwo(int n) {
3         return n > 0 && (n & (n-1)) == 0;
4     }
5 }