多源D点（邻接表+bfs）

【问题】给出一颗n个结点的树，树上每条边的边权都是1，这n个结点中有m个特殊点，请你求出树上距离这m个特殊点距离均不超过d的点的数量，包含特殊点本身。

输入：

输入第一行包含三个正整数，n、m、d分别表示树上有n个结点，其中有m个点是特殊点，d是如题所示的距离。(1<=n、m、d<=50000)

第二行m个整数，表示特殊的点的编号，编号再1-n之间。

第三行有n-1个整数，第个数表示第号结点的父亲结点的编号，同样在1-n之间。

输出：

输出仅包含一个整数，即符合题目要求的点的数量。

样例输入：

6 2 3

2 1

3 4 5 6 1

样例输出：

2

首先题目给出了说明，这棵树一共有n个节点，且边的权重为1，并且有m个特殊节点，虽然题目说了这是一个树，但是要求是找到距离m个特殊节点"均"不超过d的节点，因此如果从某一个特殊节点出发，它既可以向上查找，也可以向下查找，这明明就是一个图，题目忽悠人的好不！！！

其实想通了思路就很清晰了，首先我们建立邻接表，题目给出的节点标号是1~N，由于数组的索引从零开始，因此建立邻接表的时候要对节点标号做一个减一的操作！因为我们使用了动态数组vector，因此对于没有连接的两个节点，我们就不添加元素（并不是设置为权重为零）！还有一点需要注意：自身与自身的节点也是相连的，需要添加进去！（题目说包含特殊节点本身）

// 创建邻接表
    for (int i = ; i < list.size();i++) {
        neigbor[i+].push_back(list[i] - );
        neigbor[list[i] - ].push_back(i+);
    }
    for (int i = ; i < neigbor.size(); i++) {
        neigbor[i].push_back(i);
    }

接着我们遍历特殊节点，然后使用bfs算法来进行广度搜索，用dis变量来标记距离，如果距离大于d，就不再搜索，跳出循环！注意我们在进行广度搜索的时候要一次性处理一层节点！这也是while(size--)的作用，这种做法很类似于"之字形打印数组"。对于一个特殊节点，我们在dis变量的限制下尽可能的去搜索符合条件的节点，使用set用来判断是否访问过该节点，然后将flag中对应的节点进行自加操作！换句话说，一个特殊节点进行广度搜索时，flag数组的值最多只会加一次或者不加！

此时，flag数组表示对于某一个特殊节点，符合要求的节点有哪些（包含特殊节点本身），接着，我们用这个思路遍历每一个特殊节点就可以了！

如果特殊节点有N个，那么flag数组中值为N的标号就是满足条件的节点！也就是距离每个特殊节点距离均小于d。当然题目让返回满足条件的个数，那就数一下值为N的节点个数就行了！！！

#include <iostream>
#include <vector>
#include <queue>
#include <unordered_set>
using namespace std;
 
int main() {
    int n, m, d;
    cin >> n >> m >> d;
 
    vector<vector<int>> neigbor(n);
    vector<int> sp(m);
    vector<int> list(n - );
    for (int i = ; i < m; i++) {
        cin >> sp[i];
    }
    for (int i = ; i < n - ; i++) {
        cin >> list[i];
    }
 
    // 创建邻接表
    for (int i = ; i < list.size();i++) {
            neigbor[i+].push_back(list[i] - );
            neigbor[list[i] - ].push_back(i+);
    }
    for (int i = ; i < neigbor.size(); i++) {
        neigbor[i].push_back(i);
    }
 
    // 输出邻接表
    cout << "创建邻接表，索引从0开始，题目中编号从1开始，需要注意！" << endl;
    for (int i = ; i < neigbor.size(); i++) {
        for (int j = ; j < neigbor[i].size(); j++) {
            cout << neigbor[i][j] << " ";
        }
        cout << endl;
    }
 
    vector<int> flag(n, );
    for (int i = ; i < m; i++) {
        int dis = ;
        queue<int> que;
        unordered_set<int> set;
        que.push(sp[i] - );     // set不需要添加，由于特殊节点本身也需要访问
        while (!que.empty()) {
            int size = que.size();
 
            while (size--) {   // 类似于之字形打印二叉树，直接处理一层
                int tmp = que.front();
                que.pop();
                for (int j = ; j < neigbor[tmp].size(); j++) {
                    if (set.find(neigbor[tmp][j]) == set.end()) {
                        set.insert(neigbor[tmp][j]);
                        flag[neigbor[tmp][j]]++;
                        cout << neigbor[tmp][j] << " ! ";   // 输出满足与某一个特殊点距离不大于d的数
                    }
                }
                for (auto i : neigbor[tmp]) {
                    que.push(i);
                }
            }
            dis++;   // 距离加一
            if (dis > d) {
                break;
            }
        }
    }
    int count = ;
    for (int i = ; i < flag.size(); i++) {
        if (flag[i] == m) {
            count++;
        }
    }
    cout << endl;
    cout << "特殊点与那些数相近: ";   // 题目要求是特殊点与某些点 (均) 小于d
    for (auto i : flag) {
        cout << i << " ";
    }
    cout << endl;
    cout << count << endl;  // 输出
    system("PAUSE");
    return ;
}

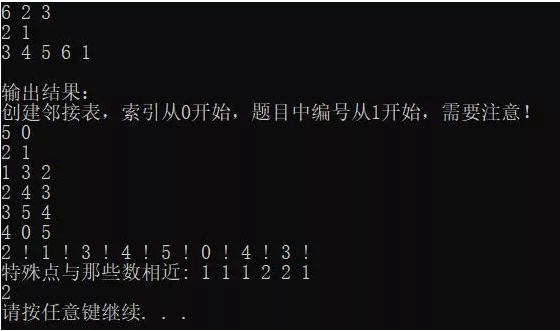
输出结果分析：
由于题中样例构建出来的树为：（注意这里索引从零开始）
1 -> 2 -> 3 -> 4 -> 5 -> 0
所以对于特殊节点1和0来说：
距离1小于d=3的有：1,2,3,4
距离0小于d=3的有：0,5,4,3
所以我们程序中flag数组应该是[1,1,1,2,2,1], 从而符合题目要求的是3和4节点！！！运行结果也表明我们的思路和程序是对的！

从5 0到4 0 5表示我们所创建的邻接表（neigbor)