洛谷 P3371 【模板】单源最短路径(堆优化dijkstra)

题目描述

如题，给出一个有向图，请输出从某一点出发到所有点的最短路径长度。

输入输出格式

输入格式：

第一行包含三个整数N、M、S，分别表示点的个数、有向边的个数、出发点的编号。

接下来M行每行包含三个整数Fi、Gi、Wi，分别表示第i条有向边的出发点、目标点和长度。

输出格式：

一行，包含N个用空格分隔的整数，其中第i个整数表示从点S出发到点i的最短路径长度（若S=i则最短路径长度为0，若从点S无法到达点i，则最短路径长度为2147483647）

输入输出样例

输入样例#1：

4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4

输出样例#1：

0 2 4 3

说明

时空限制：1000ms,128M

数据规模：

对于20%的数据：N<=5，M<=15

对于40%的数据：N<=100，M<=10000

对于70%的数据：N<=1000，M<=100000

对于100%的数据：N<=10000，M<=500000

样例说明：

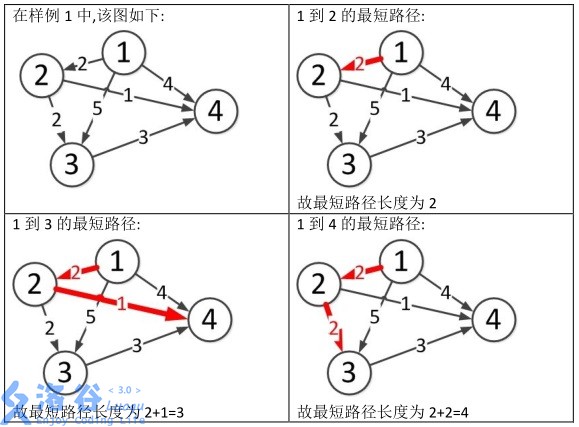
堆优化dijkstra

屠龙宝刀点击就送

#include <algorithm>
#include <cstring>
#include <ctype.h>
#include <cstdio>
#include <queue>
using namespace std;
struct Node
{
    int x,y;
    bool operator <(Node a)const
    {
        return x>a.x;
    }
};
struct node
{
    int to,dis,next;
}edge[];
priority_queue<Node>q;
void read(int &x)
{
    x=;bool f=;
    char ch=getchar();
    while(!isdigit(ch))
    {
        if(ch=='-') f=;
        ch=getchar();
    }
    while(isdigit(ch))
    {
        x=x*+ch-'';
        ch=getchar();
    }
    x=f?(~x)+:x;
}
bool vis[];
int head[],cnt,T,C,Ts,Te,dis[];
void add(int u,int v,int l)
{
    edge[++cnt].to=v;
    edge[cnt].next=head[u];
    edge[cnt].dis=l;
    head[u]=cnt;
}
int main()
{
    read(T);read(C);read(Ts);
    for(int f,t,v,i=;i<=C;i++)
    {
        read(f);read(t);read(v);
        add(f,t,v);
    //    add(t,f,v);
    }
    for(int i=;i<=T;i++) dis[i]=;
    dis[Ts]=;
    Node a;
    a.x=dis[Ts];
    a.y=Ts;
    q.push(a);
    while(!q.empty())
    {
        Node tmp=q.top();q.pop();
        if(vis[tmp.y]) continue;
        int v=tmp.y;
        vis[v]=;
        for(int i=head[v];i;i=edge[i].next)
        {
            if(dis[edge[i].to]>edge[i].dis+dis[v])
            {
                dis[edge[i].to]=edge[i].dis+dis[v];
                Node a;
                a.x=dis[edge[i].to];
                a.y=edge[i].to;
                q.push(a);
            }
        }
    }
    for(int i=;i<=T;i++) printf("%d ",dis[i]);
    return ;
}

堆优化dijkstra 548ms

#include <iostream>
#include <cstring>
#include <cstdio>

#define INF 2147483647
using namespace std;
typedef long long LL;

struct node {
    LL to,from,dis;
}e[];
bool vis[];
LL head[],ds[];
LL n,m,s,i,j,tot;
void add(LL u,LL v,LL w)
{
    tot++;
    e[tot].to=v;
    e[tot].dis=w;
    e[tot].from=head[u];
    head[u]=tot;
}
void spfa(LL k)
{
    LL l=,r=,queue[];
    for(i=;i<=n;++i)
    {
        ds[i]=INF;
        vis[i]=;
    }
    ds[k]=;
    queue[++r]=k;
    while(l<r )
    {
        LL now=queue[++l];
        vis[now]=;
        for(i=head[now];i;i=e[i].from)
        {
            LL v=e[i].to;
            if(ds[v]>ds[now]+e[i].dis)
            {
                ds[v]=ds[now]+e[i].dis;
                if(!vis[v])
                {
                    queue[++r]=v;
                    vis[v]=;
                }
            }
        }
    }
}
int main()
{
    cin>>n>>m>>s;
    LL x,y,z;
    for(i=;i<m;++i)
    {
        cin>>x>>y>>z;
        add(x,y,z);
    }
    spfa(s);
    for(i=;i<=n;++i)
    cout<<ds[i]<<" ";
}

spfa 2973ms