SVD的概念以及应用
第十四章 利用SVD简化数据
一.引言
SVD的全称是奇异值分解,SVD的作用是它能够将高维的数据空间映射到低维的数据空间,实现数据约减和去除噪声的功能。
SVD的特点主要有以下几个方面:
1.它的优点:去除噪声,简化数据,提高算法的结果
2.它的缺点:数据的转化难以理解
3.它适用的数据:数值型数据
二.SVD的作用
SVD经常用于信息检索领域,在信息检索中我们将使用了SVD方法的数据文档数据处理方式称之为隐性语义索引。隐性语义索引,它将一个文档分解为了词和词频,能够利用然后分解得到的矩阵进行奇异值分解从而或者文档的主题与概念。同时它还能够实现同义词的概念映射。
SVD也常常用于推荐系统,通过SVD对数据的约减将原始数据进行空间映射,进行降维,得到的数据可以被定义为另一种概念,可以看做是一种概念抽象的过程。
三.矩阵分解
SVD将一个矩阵(m*n)分解成三个矩阵的乘积,第一个矩阵是m*m,第二个矩阵是m*n(它是一个对角矩阵,只有对角线的元素才可能为非零,并且它的值是按照从到排列的),第三个矩阵是n*n;其中的第二个矩阵就是所说的奇异值。奇异值它能够在一定的程度上表现数据的特征,这一点和PCA中所说的特征值的概念很像,实际上奇异值和特征值也确实存在着联系。Data*dataT的特征值的开方就是data的奇异值。我们按照从大到小的顺序对奇异值进行排序,那么有可能出现奇异值为0的情况,那么这时候就说明该行的特征是多余的,我们在计算的时候就可以忽略它,这样就能够实现特征约减。
四.利用python实现SVD
利用Python事项SVD非常的简单,因为Python中的numpy中有现成的库可以调用svd.
以下是python代码:
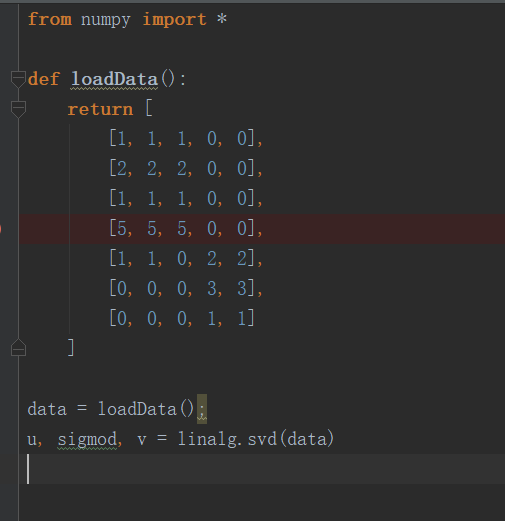
利用我们在知道奇异值之后,对于保留多少个奇异值,有很多种方法。第一种方法是比较常用的,也就是将所有的奇异值进行平方,然后依次把它们加起来知道它们的和达到总值的百分之九十,那么这些奇异值就是我们想要保留的奇异值,这种方法称之为90%energy save。另一种更加直观的方法是我们保留前若干个特征值,比如我们有一万条数据那么我们就保留前2000到三千个特征值。
五.基于协同过滤的推荐引擎
所谓的协同过滤就是利用用户和其他用户进行对比实现推荐。这个对比我们就需要用到相似度的概念,比如两个人喜欢的电影的相似度很高,那么其中一个人看过的电影就可以推荐给另一个没看过该电影的人看。
相似度的度量方式有三种:一种是1/(1+距离),第二种是皮尔逊相关系数,但是皮尔逊相关系数的值是-1到1,要对它进行0到1的归一化,那么就变成了1/2+1/2*皮尔逊相关系数值。第三种方式是余弦相似度。
以下我们用pytnon了解这三种度量方式的代码实现:
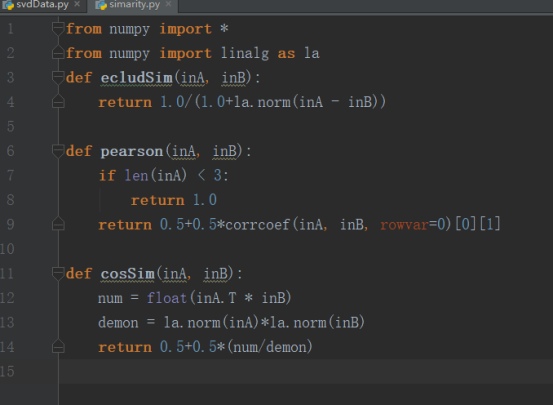
在计算相似度的时候,我们将行向量之间的相似度称之为用户相似度,将列向量之间的额相似度称之为物品相似度,具体使用用户相似度还是物品相似度取决于那个的数量更少。对于一般的推荐系统来说,商品的数量会明显的更少,所以我们倾向于选择使用商品相似度。
六.构建一个食物的推荐系统
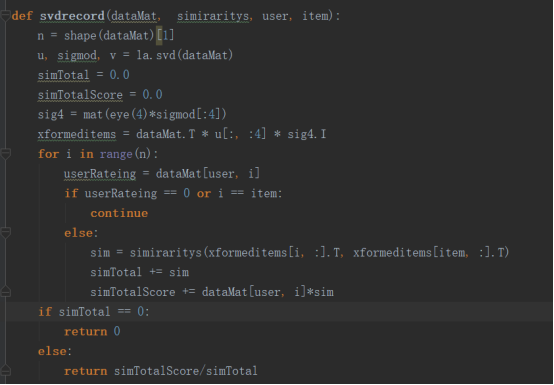
要构建一个食物的推荐系统,要分成两步:1.首先我们需要根据相似度用户对于还未吃过的食物的评分; 2.我们选出未评分的食物中,评分靠前的前几个作为我们的推荐。
以下是具体的代码:第一个步骤:
第二个步骤:
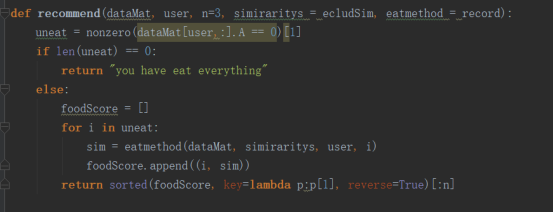
通过以上两个步骤,我们就可以得到推荐的食物的编号,和用户对它的可能评分。
这个算法还存在着一些不足,首先在实际中并不需要在每次计算得分的时候计算一次SVD;其次在计算物体相似度的时候,有很多结果是重复的,因此我们可以在计算的时候保存计算的结果,以便下一次直接调用;最后就是它可能遇到冷启动的问题。所谓的冷启动,指的是当我们新加入一个物品时,因为之前没有任何人为他评过分,因此没有物品和它相似,所以就没有办法让这个物品成为有效的物品推荐给可能喜欢它的用户。解决冷启动的问题很难,我们现在可以用基于内容的推荐来规避这个问题。
六.总结
SVD是一种去除噪声和降维的实用方法,我们可以通过SVD获取数据中的重要特征,通过保留矩阵百分之八十到百分之九十的能量,我们就可以保存重要的特征和去除噪声。SVD可以用于搜索引擎,它能够基于用户和行为数据进行协同过滤。协同过滤的核心是相似度计算,相似度的度量方式有很多种,这里列举了常用的三种。
在大数据中应用SVD技术有点困难,我们可以使用离线处理的方式,在本地先进行SVD计算,然后再应用它。
SVD的概念以及应用的更多相关文章
- 从矩阵(matrix)角度讨论PCA(Principal Component Analysis 主成分分析)、SVD(Singular Value Decomposition 奇异值分解)相关原理
0. 引言 本文主要的目的在于讨论PAC降维和SVD特征提取原理,围绕这一主题,在文章的开头从涉及的相关矩阵原理切入,逐步深入讨论,希望能够学习这一领域问题的读者朋友有帮助. 这里推荐Mit的Gilb ...
- 数据科学中需要知道的5个关于奇异值分解(SVD)的应用
介绍 "Another day has passed, and I still haven't used y = mx + b." 这听起来是不是很熟悉?我经常听到我大学的熟人抱怨 ...
- Notes About Singular Value Decomposition
A brief summary of SVD: An original matrix Amn is represented as a muliplication of three matrices: ...
- SVD奇异值分解的基本原理和运用
SVD奇异值分解: SVD是一种可靠的正交矩阵分解法.可以把A矩阵分解成U,∑,VT三个矩阵相乘的形式.(Svd(A)=[U*∑*VT],A不必是方阵,U,VT必定是正交阵,S是对角阵<以奇异值 ...
- Matrix Factorization SVD 矩阵分解
Today we have learned the Matrix Factorization, and I want to record my study notes. Some kownledge ...
- PCA本质和SVD
一.一些概念 线性相关:其中一个向量可以由其他向量线性表出. 线性无关:其中一个向量不可以由其他向量线性表出,或者另一种说法是找不到一个X不等于0,能够使得AX=0.如果对于一个矩阵A来说它的列是线性 ...
- 数值分析之奇异值分解(SVD)篇
在很多线性代数问题中,如果我们首先思考若做SVD,情况将会怎样,那么问题可能会得到更好的理解[1]. --Lloyd N. ...
- 强大的矩阵奇异值分解(SVD)及其应用
版权声明: 本文由LeftNotEasy发布于http://leftnoteasy.cnblogs.com, 本文可以被全部的转载或者部分使用,但请注明出处,如果有问题,请联系wheeleast@gm ...
- 利用奇异值分解(SVD)简化数据
特征值与特征向量 下面这部分内容摘自:强大的矩阵奇异值分解(SVD)及其应用 特征值分解和奇异值分解在机器学习领域都是属于满地可见的方法.两者有着很紧密的关系,在接下来会谈到,特征值分解和奇异值分解的 ...
随机推荐
- python字典(dictionary)使用:基本函数code实例,字典的合并、排序、copy,函数中*args 和**kwargs做形参和实参
python字典dictionary几个不常用函数例子 一.字典声明 如,d={}; d= {'x':1,'b':2} d1 = dict(x=1,y=2,z=3) d2 = dict(a=3 ...
- Html.java 存储页面信息类
Html.java 存储页面信息类 package com.iteye.injavawetrust.miner; /** * 存储页面信息类 * @author InJavaWeTrust * */ ...
- (五十五)iOS多线程之GCD
GCD的全称为Grand Central Dispatch,翻译为大中央调度,是Apple开发的一个多线程编程解决方法. 进程和线程的概念: 正在进行中的程序被称为进程,负责程序运行的内存分配,每一个 ...
- unity UGUI实现类似NGUI切换Sprite的方式
很多都是使用NGUI的习惯,因为在NGUI中所有图片都打包在一个图集中,通过更改SpriteName就可以更改图片,so,为了方便调用UGUI的sprite,我们也同样需要为其创建一个asset文件. ...
- Cocos2d中update与fixedUpdate的区别(四)
关于fixedUpdate:方法的目的 现在,想象一下在小球飞行的位置1到8之间有一个移动的平台: 该平台不停地上升和下降.有些时候小球可以不碰到而飘过平台,有些时候小球会和平台发生碰撞: 这表示小球 ...
- STL的容器算法迭代器的设计理念
1) STL的容器通过类模板技术,实现数据类型和容器模型的分离. 2) STL的迭代器技术实现了遍历容器的统一方法:也为STL的算法提供了统一性. 3) STL的函数对象实现了自定义数据类型的算法运算 ...
- 《UNIX网络编程 卷1》之"学习环境搭建"(CentOS 7)
<UNIX网络编程 卷1>的源码可以从www.unpbook.com下载得到.解压之后的目录为unpv13e. 详细步骤 编译 进入unpv13e目录,按如下步骤编译: ./configu ...
- Android高级控件(三)—— 使用Google ZXing实现二维码的扫描和生成相关功能体系
Android高级控件(三)-- 使用Google ZXing实现二维码的扫描和生成相关功能体系 摘要 现在的二维码可谓是烂大街了,到处都是二维码,什么都是二维码,扫一扫似乎已经流行到习以为常了,今天 ...
- spring的maven配置文件
spring各个包的maven配置文件 <!--spring-context--> <dependency> <groupId>org.springframewor ...
- RTMPdump(libRTMP) 源代码分析 7: 建立一个流媒体连接 (NetStream部分 2)
===================================================== RTMPdump(libRTMP) 源代码分析系列文章: RTMPdump 源代码分析 1: ...
