【题解】CF1722F L-shapes

题面传送门

其实这题根本不用搜索，有耐心即可。

可以发现，在 \(n\times m\) 范围内扫，可能合法的只有以下四种情况，其中蓝色代表示是 *，红色表示不能是 *，其中黄色五角星表示当前 \(i,j\) 的位置。

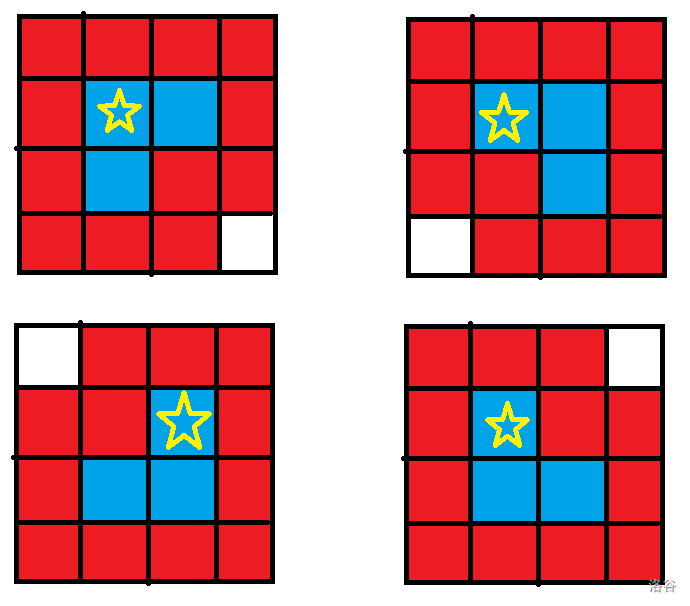
所以只要把 * 标记为 \(1\)，全图扫一遍，发现合法就给它变 \(0\)，看最后有没有 \(1\) 剩余即可。

Code：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
int T,n,m,a[55][55];
char c;
void search(int i,int j){
	if(a[i+1][j]&&a[i+1][j+1]&&!a[i-1][j-1]&&!a[i-1][j]&&!a[i-1][j+1]&&
	   !a[i][j-1]&&!a[i][j+1]&&!a[i][j+2]&&!a[i+1][j-1]&&!a[i+1][j+2]&&
	   !a[i+2][j-1]&&!a[i+2][j]&&!a[i+2][j+1]&&!a[i+2][j+2]){
		a[i][j]=a[i+1][j]=a[i+1][j+1]=0;
		return ;
	}
	if(a[i+1][j-1]&&a[i+1][j]&&!a[i-1][j-1]&&!a[i-1][j]&&!a[i-1][j+1]&&
	   !a[i][j-2]&&!a[i][j-1]&&!a[i][j+1]&&!a[i+1][j-2]&&!a[i+1][j+1]&&
	   !a[i+2][j-2]&&!a[i+2][j-1]&&!a[i+2][j]&&!a[i+2][j+1]){
		a[i][j]=a[i+1][j-1]=a[i+1][j]=0;
		return ;
	}
	if(a[i][j+1]&&a[i+1][j+1]&&!a[i-1][j-1]&&!a[i-1][j]&&!a[i-1][j+1]&&
	   !a[i-1][j+2]&&!a[i][j-1]&&!a[i][j+2]&&!a[i+1][j-1]&&!a[i+1][j]&&
	   !a[i+1][j+2]&&!a[i+2][j]&&!a[i+2][j+1]&&!a[i+2][j+2]){
		a[i][j]=a[i][j+1]=a[i+1][j+1]=0;
		return ;
	}
	if(a[i][j+1]&&a[i+1][j]&&!a[i-1][j-1]&&!a[i-1][j]&&!a[i-1][j+1]&&
	   !a[i-1][j+2]&&!a[i][j-1]&&!a[i][j+2]&&!a[i+1][j-1]&&!a[i+1][j+1]&&
	   !a[i+1][j+2]&&!a[i+2][j-1]&&!a[i+2][j]&&!a[i+2][j+1]){
		a[i][j]=a[i][j+1]=a[i+1][j]=0;
		return ;
	}
}
void solve(){
	scanf("%d%d",&n,&m);
	memset(a,0,sizeof(a));
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			cin>>c;
			if(c=='*') a[i][j]=1;
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			if(a[i][j]==1) search(i,j);
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			if(a[i][j]==1){
				printf("NO\n");
				return ;
			}
		}
	}
	printf("YES\n");
}
int main(){
	scanf("%d",&T);
	while(T--) solve();
    return 0;
}