CF995A Tesla

题目描述

Allen dreams of one day owning a enormous fleet of electric cars, the car of the future! He knows that this will give him a big status boost. As Allen is planning out all of the different types of cars he will own and how he will arrange them, he realizes that he has a problem.

Allen's future parking lot can be represented as a rectangle with 4 4 4 rows and n n n ( n≤50 n \le 50 n≤50 ) columns of rectangular spaces, each of which can contain at most one car at any time. He imagines having k k k ( k≤2n k \le 2n k≤2n ) cars in the grid, and all the cars are initially in the second and third rows. Each of the cars also has a different designated parking space in the first or fourth row. Allen has to put the cars into corresponding parking places.

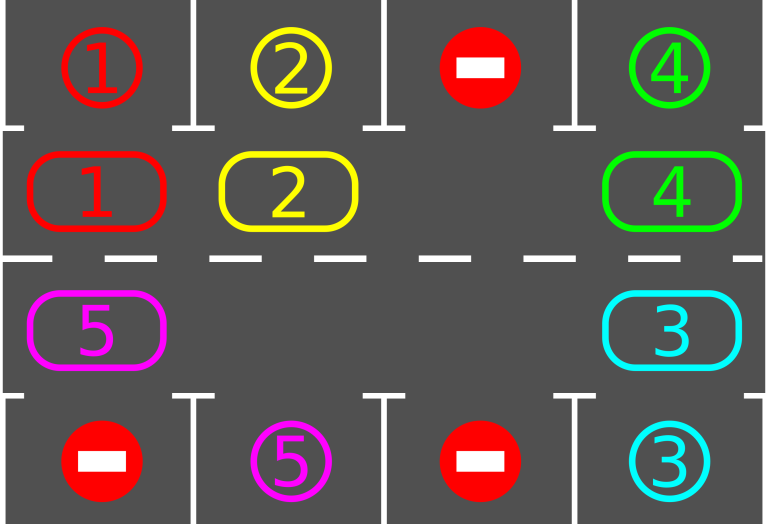Illustration to the first example.However, since Allen would never entrust his cars to anyone else, only one car can be moved at a time. He can drive a car from a space in any of the four cardinal directions to a neighboring empty space. Furthermore, Allen can only move one of his cars into a space on the first or fourth rows if it is the car's designated parking space.

Allen knows he will be a very busy man, and will only have time to move cars at most 20000 20000 20000 times before he realizes that moving cars is not worth his time. Help Allen determine if he should bother parking his cars or leave it to someone less important.

输入输出格式

输入格式：

The first line of the input contains two space-separated integers n n n and k k k ( 1≤n≤50 1 \le n \le 50 1≤n≤50 , 1≤k≤2n 1 \le k \le 2n 1≤k≤2n ), representing the number of columns and the number of cars, respectively.

The next four lines will contain n n n integers each between 0 0 0 and k k k inclusive, representing the initial state of the parking lot. The rows are numbered 1 1 1 to 4 4 4 from top to bottom and the columns are numbered 1 1 1 to n n n from left to right.

In the first and last line, an integer 1≤x≤k 1 \le x \le k 1≤x≤k represents a parking spot assigned to car x x x (you can only move this car to this place), while the integer 0 0 0 represents a empty space (you can't move any car to this place).

In the second and third line, an integer 1≤x≤k 1 \le x \le k 1≤x≤k represents initial position of car x x x , while the integer 0 0 0 represents an empty space (you can move any car to this place).

Each x x x between 1 1 1 and k k k appears exactly once in the second and third line, and exactly once in the first and fourth line.

输出格式：

If there is a sequence of moves that brings all of the cars to their parking spaces, with at most 20000 20000 20000 car moves, then print m m m , the number of moves, on the first line. On the following m m m lines, print the moves (one move per line) in the format i i i r r r c c c , which corresponds to Allen moving car i i i to the neighboring space at row r r r and column c c c .

If it is not possible for Allen to move all the cars to the correct spaces with at most 20000 20000 20000 car moves, print a single line with the integer −1 -1 −1 .

输入输出样例

输入样例#1：

4 5
1 2 0 4
1 2 0 4
5 0 0 3
0 5 0 3

输出样例#1：

6
1 1 1
2 1 2
4 1 4
3 4 4
5 3 2
5 4 2

输入样例#2：

1 2
1
2
1
2

输出样例#2：

-1

输入样例#3：

1 2
1
1
2
2

输出样例#3：

2
1 1 1
2 4 1

说明

In the first sample test case, all cars are in front of their spots except car 5 5 5 , which is in front of the parking spot adjacent. The example shows the shortest possible sequence of moves, but any sequence of length at most 20000 20000 20000 will be accepted.

In the second sample test case, there is only one column, and the cars are in the wrong order, so no cars can move and the task is impossible.

Solution：

　　本题居然是A题，然后思路确实是模拟，只不过太巧了。

　　我们固定一个方向移动所有的车子，比如顺时针，然后每次能进就进，否则就将其移动到空位上，然后重复这过程，不停绕圈就好了，可以证明即使某辆车反向偏离了终点，也最多只需要$2*50$步就能回来，所以最坏只要绕一圈能进的就进了。模拟此过程，设置一下步数限制，话说模拟题真的难写！

代码：

#include<bits/stdc++.h>
#define il inline
#define ll long long
#define For(i,a,b) for(int (i)=(a);(i)<=(b);(i)++)
#define Bor(i,a,b) for(int (i)=(b);(i)>=(a);(i)--)
using namespace std;
int n,k,a[][],tot;
struct node{
    int id,x,y;
    node(int a=,int b=,int c=){id=a,x=b,y=c;}
}ans[];

int main(){
    scanf("%d%d",&n,&k);
    For(i,,) For(j,,n) scanf("%d",&a[i][j]);
    int nx=,ny=,cnt=,sum=;
    while(cnt<=&&sum!=k){
        int tx=nx,ty,gx,gy;
        nx==?ty=ny+:ty=ny-;
        if(ty>n) tx++,ty--;
        if(ty<) tx--,ty++;
        gy=ty;
        tx==?gx=:gx=;
        if(a[tx][ty]!=){
            if(a[tx][ty]==a[gx][gy])ans[++tot]=node(a[tx][ty],gx,gy),sum++,a[tx][ty]=;
            else if(!a[nx][ny]) ans[++tot]=node(a[tx][ty],nx,ny),swap(a[tx][ty],a[nx][ny]);
        }
        nx=tx,ny=ty;
        cnt++;
    }
    if(sum==k) {
        printf("%d\n",tot);
        For(i,,tot) printf("%d %d %d\n",ans[i].id,ans[i].x,ans[i].y);
    }
    else puts("-1");
    return ;
}