抽样分布(2) t分布

定义 t分布

设X ~ N(0,1),Y ~ χ²(n),且X，Y相互独立，则称随机变量

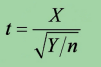
服从自由度为n的t分布（学生氏分布）

记为 t~t（n），其概率密度为

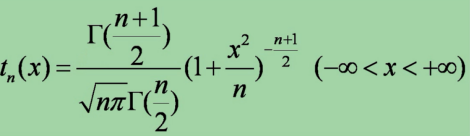
由于t_n(x)是偶函数，其图形关于y轴对称。当n趋于无穷大时，t分布以标准正态分布N（0,1）为极限分布。也就是说t分布当n~∞时，t_n(x)趋近于标准正态分布的表达式。而当n比较小的时候，t分布和标准正太分布的差距就比较大。

t分布的应用

t分布的分位点

对于一个数α（<0α<1）,怎么求数c使得概率 P{t>c}=α？这个点c称为t分布的上α分位点，记为 t_α(n)

即

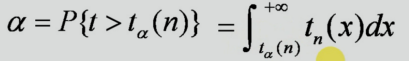
通常是已知积分值求积分下限。

----------------------------------完----------------------------------------

本文内容有参考自互联网资源。