【HDOJ6627】equation（模拟）

题意：给定n，整数序列a和b，整数C，求所有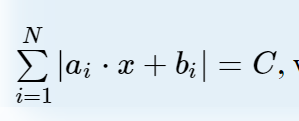成立的x

n<=1e5，1<=a[i]<=1e3，-1e3<=b[i]<=1e3，1<=C<=1e9

思路：

大概就照每条直线的零点分段，维护一下系数和常数项

特判的地方挺多，精度也要注意，写起来像计算几何

感觉这种麻烦的东西应该有模板

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 typedef unsigned int uint;
 typedef unsigned long long ull;
 typedef pair<int,int> PII;
 typedef pair<ll,ll> Pll;
 typedef vector<int> VI;
 typedef vector<PII> VII;
 #define N  1100000
 #define M  4100000
 #define fi first
 #define se second
 #define MP make_pair
 #define pi acos(-1)
 #define mem(a,b) memset(a,b,sizeof(a))
 #define rep(i,a,b) for(int i=(int)a;i<=(int)b;i++)
 #define per(i,a,b) for(int i=(int)a;i>=(int)b;i--)
 #define lowbit(x) x&(-x)
 #define Rand (rand()*(1<<16)+rand())
 #define id(x) ((x)<=B?(x):m-n/(x)+1)
 #define ls p<<1
 #define rs p<<1|1

 const ll MOD=,inv2=(MOD+)/;
       double eps=1e-;
       int INF=1e9;

 struct arr
 {
     ll a,b;
 }c[N],ans[N];

 bool cmp(arr a,arr b)
 {
     return a.b*b.a>b.b*a.a;
 }

 ll read()
 {
    ll v=,f=;
    char c=getchar();
    while(c<||<c) {if(c=='-') f=-; c=getchar();}
    while(<=c&&c<=) v=(v<<)+v+v+c-,c=getchar();
    return v*f;
 }

 ll gcd(ll x,ll y)
 {
     if(y==) return x;
     return gcd(y,x%y);
 }

 int xiaoyu(ll x1,ll y1,ll x2,ll y2)
 {
     //printf("xiaoyu %I64d %I64d %I64d %I64d\n",x1,y1,x2,y2);
     int p=-;
     ll t=x1*y2-y1*x2;
     if(t==) return ;
     if(t<) p=-p;
     if(y1*y2<) p=-p;
     return (p==);
 }

 int main()
 {
     //freopen("1.in","r",stdin);
     int cas=read();
     while(cas--)
     {
         int n;
         scanf("%d",&n);
         ll C=read();
         rep(i,,n)
         {
             c[i].a=read();
             c[i].b=read();
         }
         sort(c+,c+n+,cmp);
         //rep(i,1,n) printf("%I64d %I64d\n",c[i].a,c[i].b);
         int m=;
         ll sa=,sb=;
         rep(i,,n)
         {
             sa-=c[i].a;
             sb-=c[i].b;
         }
         //printf("sa=%I64d C-sb=%I64d\n",sa,C-sb);
         int flag=;
         if(sa==&&C-sb==) flag=;
         if(xiaoyu(C-sb,sa,-c[].b,c[].a))
         {
             if(sa==&&C-sb!=) continue;
             m++;
             ll t=gcd(abs(C-sb),abs(sa));
             //printf("t=%I64d\n",t);
             ans[m].a=(C-sb)/t;
             ans[m].b=sa/t;
             if(ans[m].b<)
             {
                 ans[m].a=-ans[m].a;
                 ans[m].b=-ans[m].b;
             }
         }
         c[n+].a=-1e15; c[n+].b=;
         rep(i,,n)
         {
             sa+=2ll*c[i].a;
             sb+=2ll*c[i].b;
             //printf("sa=%I64d C-sb=%I64d\n",sa,C-sb);
             if(sa==&&C-sb==)
             {
                 flag=;
                 break;
             }
             if(sa==&&C-sb!=) continue;
             if(xiaoyu(C-sb,sa,-c[i].b,c[i].a)==&&xiaoyu(C-sb,sa,-c[i+].b,c[i+].a))
             {
                 if(m>=&&(C-sb)*ans[m].b==sa*ans[m].a) continue;
                 m++;
                 ll t=gcd(abs(C-sb),abs(sa));
                 ans[m].a=(C-sb)/t;
                 ans[m].b=sa/t;
                 if(ans[m].b<)
                 {
                     ans[m].a=-ans[m].a;
                     ans[m].b=-ans[m].b;
                 }
             }
         }
         if(flag)
         {
             printf("-1\n");
             continue;
         }
         if(m==)
         {
             printf("0\n");
             continue;
         }

         printf("%d ",m);
         rep(i,,m-) printf("%I64d/%I64d ",ans[i].a,ans[i].b);
         printf("%I64d/%I64d\n",ans[m].a,ans[m].b);
     }

     return ;
 }