模板 - 强连通分量 - Kosaraju

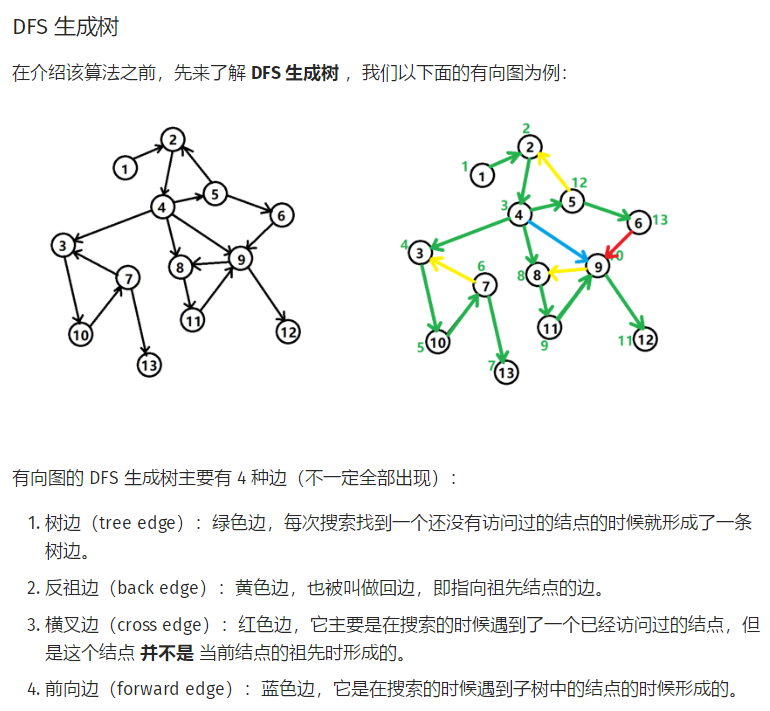
Kosaraju算法 O(n+m)

vector<int> s;

void dfs1(int u) {
    vis[u] = true;
    for (int v : g[u])
        if (!vis[v])
            dfs1(v);
    s.push_back(u);
}

void dfs2(int u) {
    color[u] = sccCnt;
    for (int v : g2[u])
        if (!color[v])
            dfs2(v);
}

void Kosaraju() {
    s.clear();
    for (int i = 1; i <= n; ++i)
        if (!vis[i])
            dfs1(i);
    sccCnt = 0;
    for (int i = n; i >= 1; --i)
        if (!color[s[i]]) {
            ++sccCnt;
            dfs2(s[i])
        }
}

https://www.luogu.org/problem/P1262

首先考虑假如一个间谍没办法被揭发不能被贿赂，也就是他不是可行的入口点也没有别人指向他，那么无解。

否则可能要若干个入度为0的点，这些点必须被贿赂，且这些点能到达的点不需要再贿赂。

否则一定存在环，或者多个环交在一起的，而这些环都是同一强连通分量内的，找这个强连通分量里面的最小的那个。

有个问题就是加入强连通分量里的都不能被贿赂就很尴尬了，所以干脆一开始就把强连通分量用编号最小的点来代替？

这个就是在dfs1的时候把额外的信息维护好了，然后在dfs2的时候维护这个强连通分量的最小花费以及假如是INF的话的最小id。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

const int MAXN = 3005;
const int INF = 0x3f3f3f3f;

int n,w[MAXN], indeg[MAXN];

vector<int> G[MAXN], G2[MAXN];

//从i点出发的连通分量，染色为c1[i]
int c1[MAXN],cntc1;
bool visc1[MAXN];

//i点所在的强连通分量，染色为c2[i]
int c2[MAXN],cntc2;
int minCost[MAXN], minID[MAXN];

int s[MAXN],cnts;

void dfs1(int u,int c) {
    c1[u]=c;
    for (int v : G[u])
        if (!c1[v])
            dfs1(v,c);
    s[++cnts]=u;
}

void dfs2(int u, int &minid) {
    c2[u] = cntc2;
    minCost[cntc2] = min(minCost[cntc2], w[u]);
    minid = min(minid, minID[cntc2]);
    for (int v : G2[u])
        if (!c2[v])
            dfs2(v, minid);
}

void Kosaraju(ll &sum, int &minid) {
    minid = INF;
    for (int i = 1; i <= n; ++i)
        if (!c1[i]){
            ++cntc1;
            dfs1(i,cntc1);
        }
    for (int i = n; i >= 1; --i) {
        if (!c2[s[i]]) {
            ++cntc2;
            minCost[cntc2] = INF;
            minID[cntc2] = INF;
            dfs2(s[i], minid);
        }
        if(minCost[cntc2] == INF)
            minid = min(minid, minID[cntc2]);
        else{
            if(!visc1[c1[s[i]]]){
                visc1[c1[s[i]]]=true;
                sum += minCost[cntc2];
            }
        }
    }
}

int main() {
#ifdef Yinku
    freopen("Yinku.in", "r", stdin);
#endif // Yinku
    int p;
    scanf("%d%d", &n, &p);
    memset(w, INF, sizeof(w[0]) * (n + 1));
    for(int i = 1; i <= p; ++i) {
        int id, c;
        scanf("%d%d", &id, &c);
        w[id] = c;
    }
    int m;
    scanf("%d", &m);
    for(int i = 1; i <= m; ++i) {
        int u, v;
        scanf("%d%d", &u, &v);
        ++indeg[v];
        G[u].emplace_back(v);
        G2[v].emplace_back(u);
    }
    ll sum = 0;
    for(int i = 1; i <= n; ++i) {
        if(indeg[i] == 0 && w[i] == INF) {
            puts("NO");
            printf("%d\n", i);
            return 0;
        } else if(indeg[i] == 0) {
            //处理了所有入度为0的点，剩下的必定是独立环
            ++cntc1;
            dfs1(i,cntc1);
            visc1[cntc1]=true;
            sum += w[i];
        }
    }
    int minid;
    Kosaraju(sum, minid);
    if(minid == INF) {
        puts("YES");
        printf("%lld\n", sum);
    } else {
        //某个强连通分量里有不能被贿赂的点
        puts("NO");
        printf("%d\n", minid);
    }
    return 0;
}

https://www.luogu.org/problem/P1262

首先每个入链必须都要给一套，然后剩下的必有环，或者环带出链。这样就很麻烦了。把整个图的强连通分量缩成点之后，变成若干独立的链（这些链可能会交叉）。入度为0的点就是子问题1的答案。子问题2里面，考虑每次多连一条边可以消除至多1个入度为0的和1个出度为0的（就算是孤立点，也是要连一条入边一条出边才能强连通），整个图强连通肯定存在一种首尾相连的办法。答案为两者间的最大值。特例是缩点之后假如只剩下一个点，那么不需要连边。

注意一定要先处理掉链，然后进去找强连通分量，成功缩点之后新图的G的边记得要去重，方便的话可以用set，怕卡就vector然后sortunique。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

const int MAXN = 105;
const int INF = 0x3f3f3f3f;

int n, w[MAXN], indeg[MAXN];

vector<int> G[MAXN], G2[MAXN];

//从i点出发的连通分量，染色为c1[i]
int c1[MAXN], cntc1;

//i点所在的强连通分量，染色为c2[i]
int c2[MAXN], cntc2;

//第i个强连通分量内的点
vector<int> C2[MAXN];

int s[MAXN], cnts;

void dfs1(int u) {
    c1[u] = cntc1;
    for (int v : G[u])
        if (!c1[v])
            dfs1(v);
    s[++cnts] = u;
}

void dfs2(int u) {
    C2[cntc2].push_back(u);
    c2[u] = cntc2;
    for (int v : G2[u])
        if (!c2[v])
            dfs2(v);
}

void Kosaraju() {
    //再计算环
    for (int i = 1; i <= n; ++i)
        if (!c1[i]) {
            ++cntc1;
            dfs1(i);
        }
    for (int i = n; i >= 1; --i)
        if (!c2[s[i]]) {
            ++cntc2;
            dfs2(s[i]);
        }
}

set<int> G3[MAXN];
int indeg3[MAXN], outdeg3[MAXN];

int main() {
#ifdef Yinku
    freopen("Yinku.in", "r", stdin);
#endif // Yinku
    scanf("%d", &n);
    for(int u = 1; u <= n; ++u) {
        int v;
        while(1) {
            scanf("%d", &v);
            if(!v)
                break;
            G[u].push_back(v);
            G2[v].push_back(u);
            ++indeg[v];
        }
    }
    for (int i = 1; i <= n; ++i)
        if (!c1[i] && indeg[i] == 0) {
            ++cntc1;
            dfs1(i);
        }
    Kosaraju();
    if(cntc2 == 1) {
        //只有一个强连通分量
        printf("%d\n%d\n", 1, 0);
    } else {
        for(int u = 1; u <= cntc2; ++u) {
            for(auto ui : C2[u]) {
                for(auto vi : G[ui]) {
                    if(c2[vi] != u) {
                        G3[u].insert(c2[vi]);
                        ++indeg3[c2[vi]];
                        ++outdeg3[u];
                    }
                }
            }
        }

        /*for(int i = 1; i <= n; ++i) {
            printf("%d:%d\n", i, c2[i]);
        }
        puts("");

        for(int i=1;i<=cntc2;++i){
            printf("u=%d\n",i);
            for(auto v:G3[i])
                printf("  v=%d\n",v);
        }*/

        int in0 = 0, out0 = 0;
        for(int u = 1; u <= cntc2; ++u) {
            if(indeg3[u] == 0)
                ++in0;
            if(outdeg3[u] == 0)
                ++out0;
        }
        printf("%d\n%d\n", in0, max(in0, out0));
    }
    return 0;
}