重新网格化（Remesh）

Remesh并没有一个严格的定义，简单的讲，Remesh就是从一个输入网格生成另一个网格，并且满足一定的要求。根据网格改动大小，可以分为这么几类：

保持顶点拓扑和几何信息，优化网格连接关系
保持顶点拓扑信息，同时优化顶点几何和网格连接关系
顶点重采样，优化网格连接关系

Remesh对原网格的改动比较大，实际应用中要谨慎使用。尽量使用改动比较小的Remesh方法。

Delaunay三角化

Delaunay三角化，是点云的一种三角化方法，它具有某些好的性质：

网格中的最小角最大化
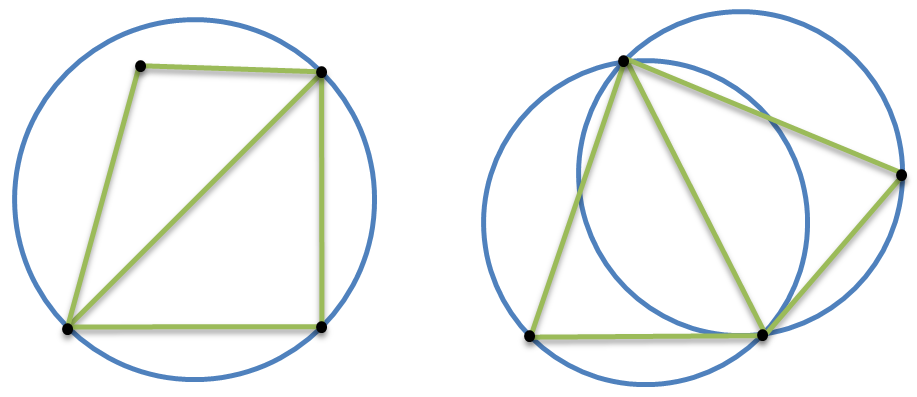
任意三角形的外接圆内不含三角形以外的顶点
三角化的网格是点云的凸包
最大化所有三角面片的内切圆的平均值
其它......

带约束的Delaunay三角化

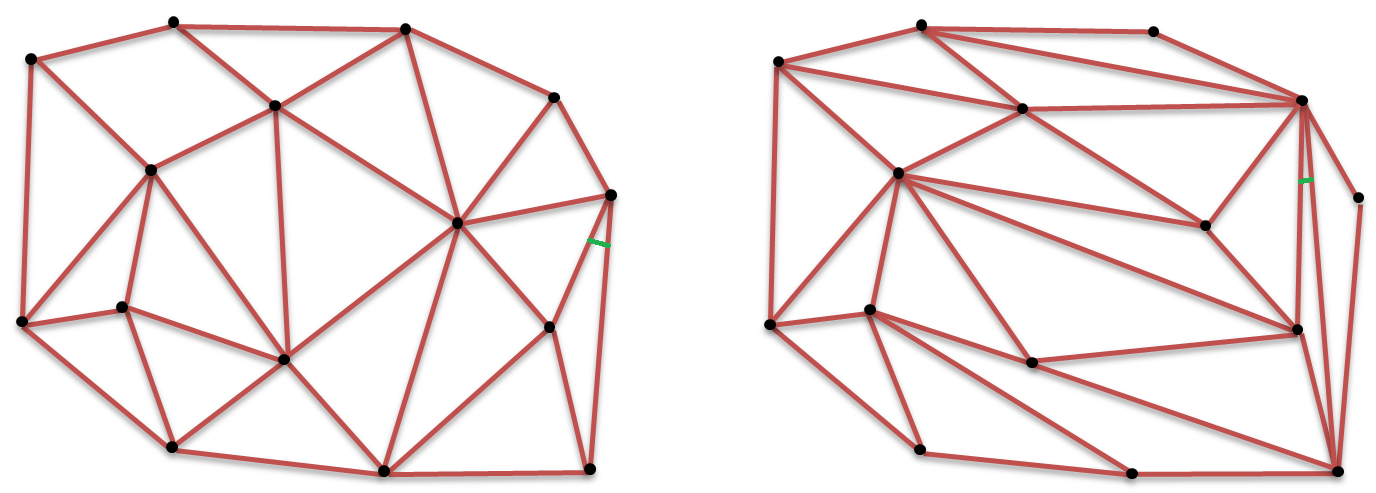
有时候，点云包含一些线段连接约束，如下左图所示。有些约束边并不满足Denaulay性质，所以，它并不能得到整体的Delaunay三角化结果(如下中图是点云的一个Delaunay三角化结果)。我们可以放开一些Delaunay性质约束，使其尽量的接近Delaunay三角化。下右图是一个带约束的Denaulay三角化的结果。可以比较一下中图和右图的结果差异。

Delaunay网格优化

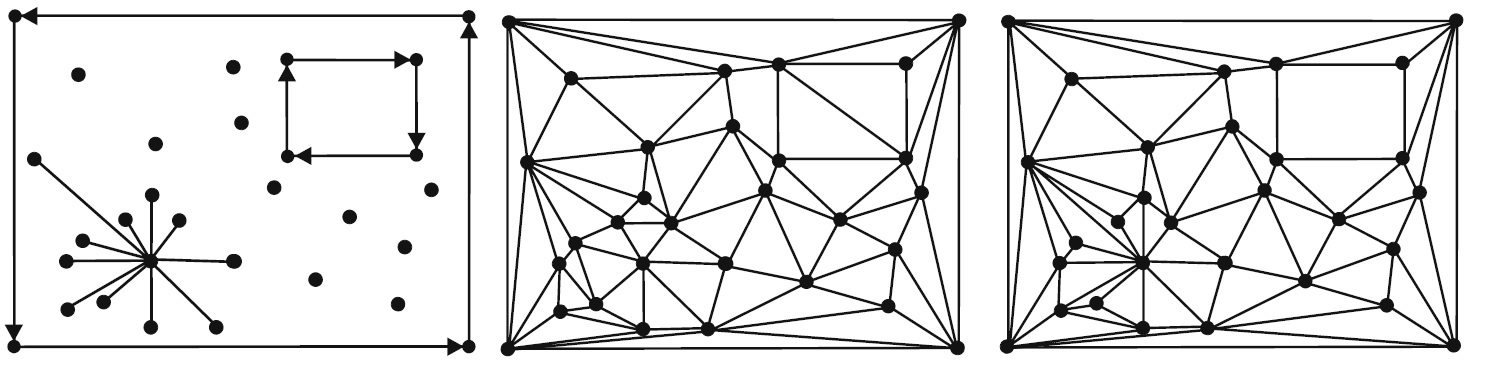
Delaunay优化，可以优化网格的连接关系，减少狭长三角形，保持网格顶点数目和位置不变。如下图所示，图2和图3是图1点云不同的三角化结果。图2经过一系列拓扑优化，如Delaunay边翻转操作，得到图3的高质量网格。

Delaunay优化只改变了网格顶点的连接关系，一般是局部的Delaunay边翻转。由于顶点保持不变，它可以极大可能的保持住原始网格的几何信息。缺点是，在顶点分布很差的情况下，优化的效果有限。

Voronoi图

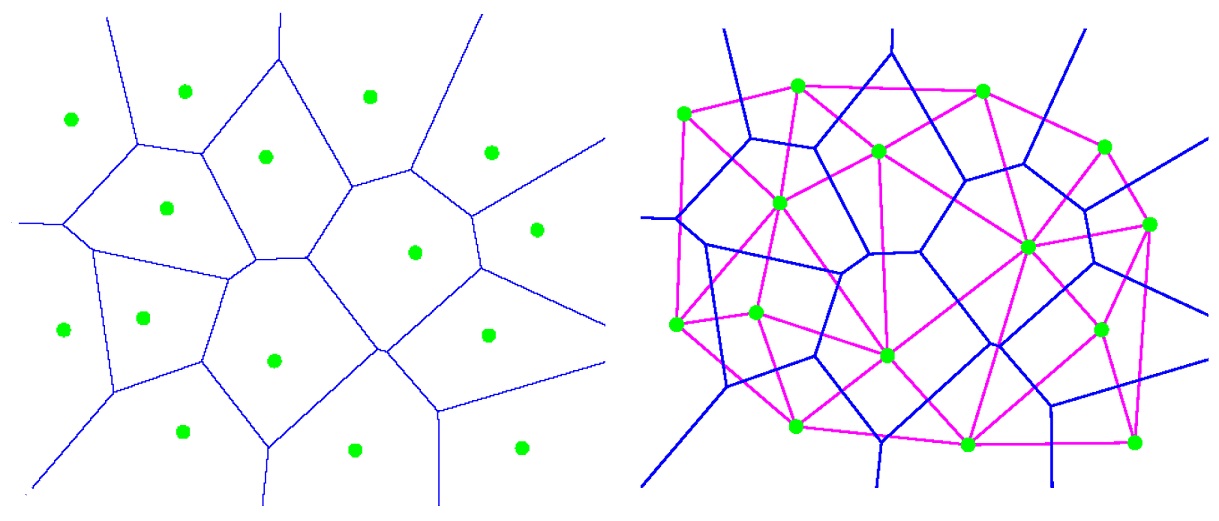
给定一群平面（或曲面）的点，其Voronoi图，把平面（或者曲面）分隔成一块一块的区域，每个区域包含一个点，并且这块区域到所有点的最近点为其所包含的点。如图左所示。这些线也是相邻两点的垂直平分线。如果是曲面上的点，点之间的距离为曲面的测地距离。

Voronoi图和Delaunay三角化的图，互为对偶图。如图右所示。

重心Voronoi图

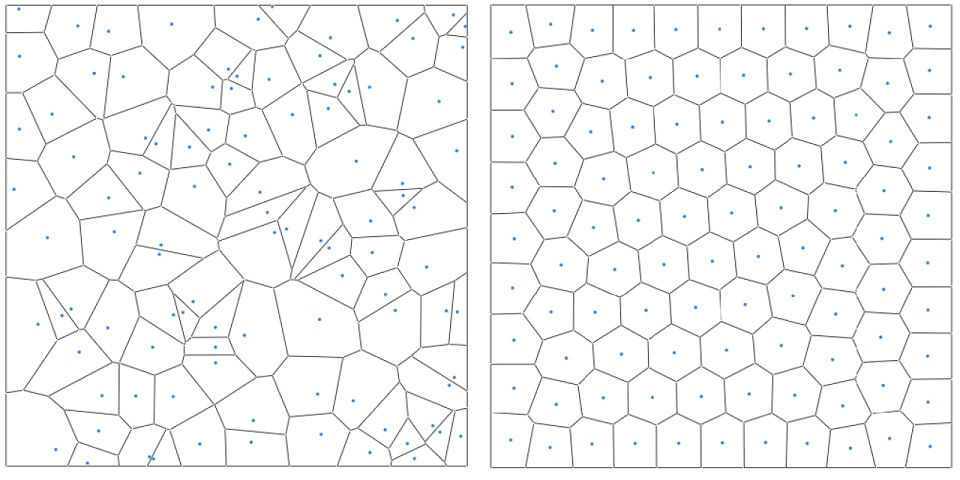
重心Voronoi图，是一种特殊的Voronoi图，其每个区域的重心和其对应点重合。如右图所示，这就是一个重心Voronoi图。

重心Voronoi优化

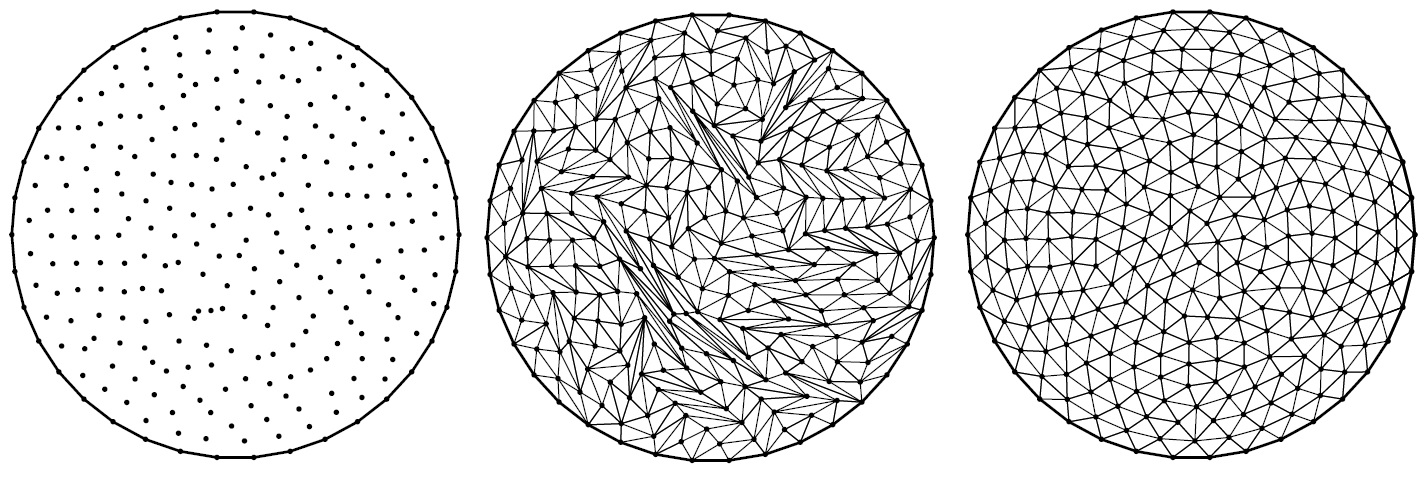
重心Voronoi优化，可以减少狭长三角形。它和Delaunay优化的区别是，它不仅优化网格顶点的连接关系，还要优化顶点的位置。如下图1所示，虽然这是一个Delaunay三角化，但明显可以看出其网格质量很很差的，经过一系列几何优化（如重心Voronoi优化）后，顶点分布更加均匀，然后再做一个Delaunay三角化就得到了图2的结果。

重心Voronoi优化，虽然可以优化顶点分布，但其优化程度有限，在顶点分布极不均匀的情况下，效果还是不理想的。

重新网格化(Remesh)

这里的Remesh，主要是指顶点重新采样的类型。前面提到的Delaunay优化和重心Voronoi优化也属于Remesh的范畴，但它们对顶点分布的优化能力有限。

Remesh的目标有很多种，一般是应用驱动的，不同的应用所需要的性质是有差别的，即使是同一个性质，有时候是硬约束，有时候是软约束。常见的一些性质有：

新网格是原网格的一个好的逼近
新网格复杂度（网格顶点或面片数量）
网格面片质量满足一定的要求：避免狭长和退化面片；顶点度数为6；顶点分布满足均匀分布或几何相关的各项异性分布；网格边长要求。
保持特征边
新网格要保持流形结构

通常情况下，这些性质很难同时满足，有些性质是矛盾的：

网格复杂度与逼近误差
网格顶点均匀分布与逼近误差
保持特征边与网格面片质量

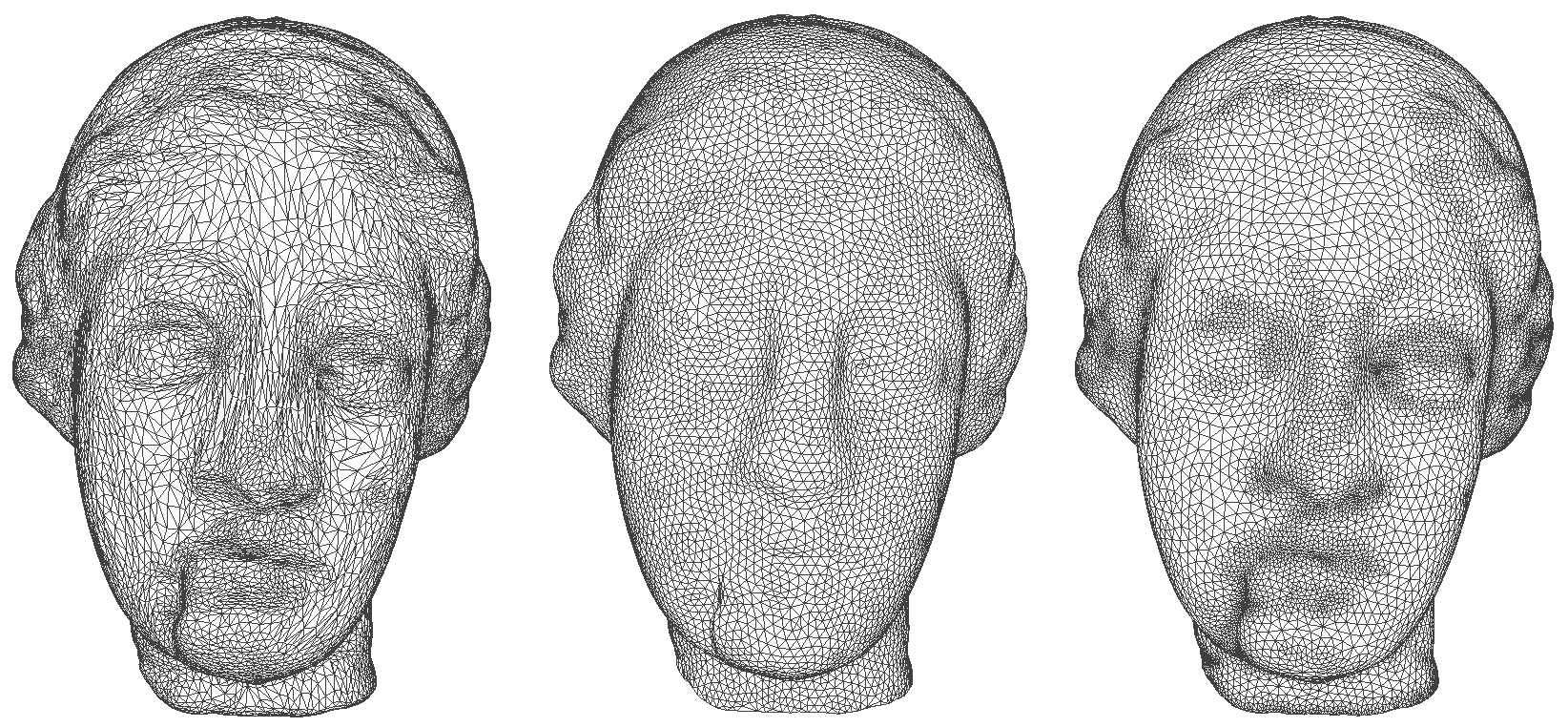
Remesh的方法，大致可以分为局部和全局的：

局部方法：经过一系列的局部拓扑和几何操作的迭代，来Remesh整个网格。它的优点是计算速度比较快，容易实现；缺点是缺乏整体质量的把控，是一种启发式方法。
全局方法：一般指把网格分割成一片一片的，然后分片参数化子网格。参数化的过程中，保持住边界的连续性。也有一些全局参数化的方法，不要网格分割这一步。最后再把参数域的网格拓扑结构反映射回原网格。它的优点是网格的全局质量容易把控，缺点也显而易见，强烈的依赖参数化方法，稳定高质量的实现会比较困难。

有兴趣的读者，欢迎参考视频版本：Delaunay三角化；Voronoi图