Codeforces 789e The Great Mixing （bitset dp 数学）

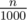Sasha and Kolya decided to get drunk with Coke, again. This time they have k types of Coke. i-th type is characterised by its carbon dioxide concentration . Today, on the party in honour of Sergiy of Vancouver they decided to prepare a glass of Coke with carbon dioxide concentration . The drink should also be tasty, so the glass can contain only integer number of liters of each Coke type (some types can be not presented in the glass). Also, they want to minimize the total volume of Coke in the glass.

Carbon dioxide concentration is defined as the volume of carbone dioxide in the Coke divided by the total volume of Coke. When you mix two Cokes, the volume of carbon dioxide sums up, and the total volume of Coke sums up as well.

Help them, find the minimal natural number of liters needed to create a glass with carbon dioxide concentration 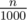. Assume that the friends have unlimited amount of each Coke type.

Input

The first line contains two integers n, k (0 ≤ n ≤ 1000, 1 ≤ k ≤ 1e6) — carbon dioxide concentration the friends want and the number of Coke types.

The second line contains k integers a1, a2, ..., ak (0 ≤ ai ≤ 1000) — carbon dioxide concentration of each type of Coke. Some Coke types can have same concentration.

Output

Print the minimal natural number of liter needed to prepare a glass with carbon dioxide concentration 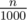, or -1 if it is impossible.

Examples

input

400 4
100 300 450 500

output

2

input

50 2
100 25

output

3

Note

In the first sample case, we can achieve concentration 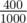 using one liter of Coke of types  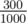and : .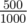

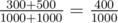In the second case, we can achieve concentration 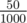 using two liters of  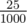type and one liter of  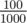type: .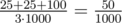

给你k个不同浓度（浓度可能重复哦）的饮料，再给你一个目标浓度n，只允许让你用已给的k种饮料，每个只允许用整数升，问你最少用多少升饮料就能配成目标浓度。

首先我们发现如果要满足条件，我假设第i种饮料取k_i升，则

这样我们对于每个a[i]，我们a[i]-=n，然后问题转换成了我们在这个数中选数，每个数能选多次，最后让所有选出的数的sum=0

这像不像一个背包问题？但是我们注意到n的范围是1e6，那么如果ans存在，ans最大是多少呢？     1000！

因为假设目标浓度为b，有小于b的浓度a，大于b的浓度c。我们只需要（c-b）升a与(b-a)升c就能配成b！  [(c-b)*a+(b-a)*c]/[(c-b)+(b-a)]=b

此时我们用了(c-b)+(b-a)=a-c升，最大就是1000了

现在大体思路已经确定，两层for循环，外层循环升(1~1005)，内层循环a[i]。此时复杂度是1e9。

我们这时用bitset数组优化。bitset是一堆0 1 的数组，在进行位运算时很快，因为只有0 1 可以用来标记状态的有无。

我们开一个2*2000的bitset，我们将0这个位置向左移动1000位来避免负数。每次更新dp[t]数组就行了。

我代码里面 n  k的定义是反着的...

代码如下：

 #include <bits/stdc++.h>

 using namespace std;
 const int maxn=1e6+;
 int n,k;
 int a[maxn];
 bitset<> dp[];
 int main()
 {
     //freopen("de.txt","r",stdin);
     while (~scanf("%d%d",&k,&n)){
         for (int i=;i<n;++i)
             scanf("%d",&a[i]),a[i]-=k;
         sort(a,a+n);
         n=unique(a,a+n)-a;//将a去下重
         int t=;
         dp[][]=;//将初始位置标记为1,即可以被vis到
         for (int i=;i<=;++i){//循环升(步数)
             for (int j=;j<n;++j){
                 if (a[j]<)//(如果a[j]<0)
                     dp[t]|=dp[-t]>>(-a[j]);//将当前状态向右移-a[j]位，让下一状态继承这个变化
                 else
                     dp[t]|=dp[-t]<<(a[j]);//将当前状态向左移a[j]位
             }
             if (dp[t][]!=){//如果此时回到了初始状态，找到了答案
                 cout<<i<<endl;
                 return ;
             }
             t=-t;
             dp[t].reset();//每次将上一状态清空，用滚动数组
         }
         printf("-1\n");
     }
     return ;
 }