leetcode-mid-math-172. Factorial Trailing Zeroes-NO-？？？？

mycode

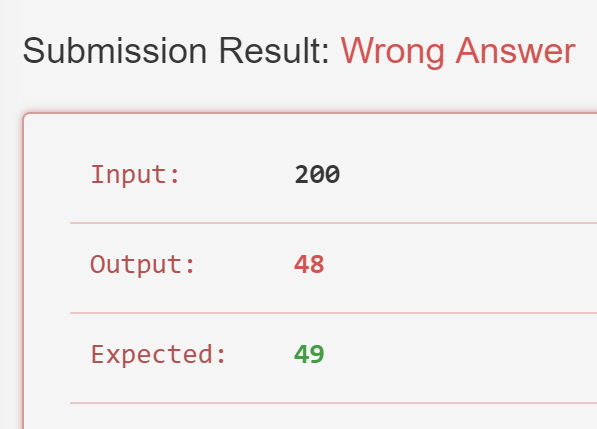
问题：为甚在小于200的时候，答案ok，大于等于200的时候，就少一个1？？？

class Solution(object):
    def trailingZeroes(self, n):
        """
        :type n: int
        :rtype: int
        """
        if n<1:
            return 0
        k = 5
        count = 0
        while n // k:
            count += n // k
            k = k*k
        #count_2 = 1 if n%10==0 else 0
        #if n < 200:
        #    return count
        return count
    #30-》 30 .。25.。。20。。15.。。没有数25中的另外一个5！
    

参考

class Solution(object):
    def trailingZeroes(self, n):
        """
        :type n: int
        :rtype: int
        """
        return 0 if n == 0 else n / 5 + self.trailingZeroes(n / 5)