CQOI2005 三角形面积并 和 POJ1177 Picture

1845: [Cqoi2005] 三角形面积并

Time Limit: 3 Sec  Memory Limit: 64 MB
Submit: 1664  Solved: 443
[Submit][Status][Discuss]

Description

给出n个三角形，求它们并的面积。

Input

第一行为n(N < = 100)， 即三角形的个数
以下n行，每行6个整数x1, y1, x2, y2, x3, y3，代表三角形的顶点坐标。坐标均为不超过10 ^ 6的实数，输入数据保留1位小数

Output

输出并的面积u, 保留两位小数

Sample Input

2

0.0 0.0 2.0 0.0 1.0 1.0

1.0 0.0 3.0 0.0 2.0 1.0

Sample Output

1.75

HINT

Source

[Submit][Status][Discuss]

HOME
Back

Claris的题解

求出所有交点后从左往右扫描线，用每段的中位线去截所有三角形，算出长度并后乘以该段长度即可，时间复杂度\(O(n^3\log n)\)。

#include<bits/stdc++.h>
#define rg register
#define il inline
#define co const
template<class T>il T read(){
    rg T data=0,w=1;rg char ch=getchar();
    while(!isdigit(ch)) {if(ch=='-') w=-1;ch=getchar();}
    while(isdigit(ch)) data=data*10+ch-'0',ch=getchar();
    return data*w;
}
template<class T>il T read(rg T&x) {return x=read<T>();}
typedef long long ll;
using namespace std;

co double eps=1e-9,INF=1e6;
il int sig(double x) {return abs(x)<eps?0:(x>0?1:-1);}
struct P{double x,y;};
il bool cmp(co P&u,co P&v) {return u.x<v.x;}
il P operator+(co P&u,co P&v) {return (P){u.x+v.x,u.y+v.y};}
il P operator-(co P&u,co P&v) {return (P){u.x-v.x,u.y-v.y};}
il P operator*(co P&u,double k) {return (P){u.x*k,u.y*k};}
il double cross(co P&u,co P&v) {return u.x*v.y-u.y*v.x;}
il bool has_intersection(co P&a,co P&b,co P&p,co P&q){
	return sig(cross(b-a,p-a))*sig(cross(b-a,q-a))<0&&
		   sig(cross(q-p,a-p))*sig(cross(q-p,b-p))<0;
}
il P line_intersection(co P&a,co P&b,co P&p,co P&q){
	return a+(b-a)*(cross(p-a,q-p)/cross(b-a,q-p));
}

co int N=300;
int n,m;
P tri[N][4],seg[N];
double px[N*N],ans;
double cal(double x){
	P D=(P){x,-INF},U=(P){x,INF};
	int m=0;
	for(int i=0,k=0;i<n;++i,k=0){
		double y[2];
		for(int j=0;j<3;++j)if(has_intersection(tri[i][j],tri[i][j+1],D,U))
			y[k++]=line_intersection(tri[i][j],tri[i][j+1],D,U).y;
		if(k) seg[m++]=(P){min(y[0],y[1]),max(y[0],y[1])};
	}
	if(m>1) sort(seg,seg+m,cmp);
	double l=-INF,r=-INF,t=0;
	for(int i=0;i<m;++i){
		if(sig(seg[i].x-r)>0) t+=r-l,l=seg[i].x;
		r=max(r,seg[i].y);
	}
	return t+r-l;
}
int main(){
//	freopen(".in","r",stdin),freopen(".out","w",stdout);
	read(n);
	for(int i=0;i<n;++i){
		for(int j=0;j<3;++j)
			scanf("%lf%lf",&tri[i][j].x,&tri[i][j].y),px[m++]=tri[i][j].x;
		tri[i][3]=tri[i][0];
	}
	for(int i=0;i<n;++i)for(int j=0;j<i;++j)
		for(int k=0;k<3;++k)for(int l=0;l<3;++l)
			if(has_intersection(tri[i][k],tri[i][k+1],tri[j][l],tri[j][l+1]))
				px[m++]=line_intersection(tri[i][k],tri[i][k+1],tri[j][l],tri[j][l+1]).x;
	sort(px,px+m);
	for(int i=1;i<m;++i)if(sig(px[i]-px[i-1]))
		ans+=(px[i]-px[i-1])*cal((px[i]+px[i-1])/2);
	return printf("%.2lf\n",ans-eps),0;
}

Picture

Language:Default

Picture

Time Limit: 2000MS		Memory Limit: 10000K
Total Submissions: 14427		Accepted: 7542

Description

A number of rectangular posters, photographs and other pictures of the same shape are pasted on a wall. Their sides are all vertical or horizontal. Each rectangle can be partially or totally covered by the others. The length of the boundary of the union of all rectangles is called the perimeter.



Write a program to calculate the perimeter. An example with 7 rectangles is shown in Figure 1.



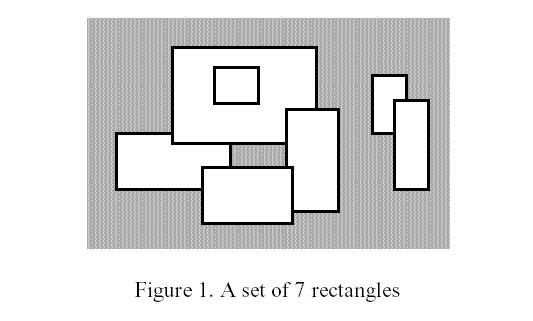
The corresponding boundary is the whole set of line segments drawn in Figure 2.



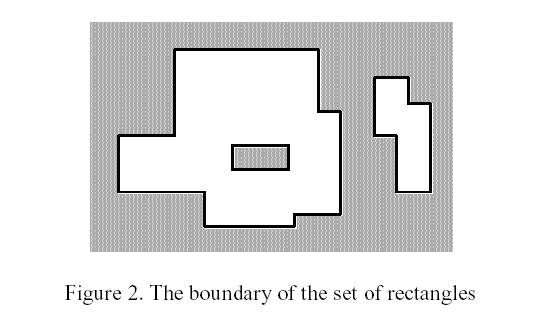
The vertices of all rectangles have integer coordinates.

Input

Your program is to read from standard input. The first line contains the number of rectangles pasted on the wall. In each of the subsequent lines, one can find the integer coordinates of the lower left vertex and the upper right vertex of each rectangle. The values of those coordinates are given as ordered pairs consisting of an x-coordinate followed by a y-coordinate.



0 <= number of rectangles < 5000

All coordinates are in the range [-10000,10000] and any existing rectangle has a positive area.

Output

Your program is to write to standard output. The output must contain a single line with a non-negative integer which corresponds to the perimeter for the input rectangles.

Sample Input

7
-15 0 5 10
-5 8 20 25
15 -4 24 14
0 -6 16 4
2 15 10 22
30 10 36 20
34 0 40 16

Sample Output

228

Source

IOI 1998

给出多个矩形坐标，求所有矩形的组合体的周长

A_Mango的题解

这道题的突破口是线扫描，假想一条垂直于y轴的线从下往上扫描，以矩形x轴方向的边为事件，这样只要知道当前发生事件时矩形的覆盖x轴的长度(为了计算x轴方向的边)，以及由几块孤立的区域组成(为了计算y轴方向的边)，但是问题就是如何在每次更新事件时更新这两个属性

这就到了线段树出场，因为如果要维护这2个属性，必须要在矩形下边的边时加入它，在上边时把它删除，能快速做到对一个线段快速修改就是线段树了，而且对于维护一个区域内的线段的总长度，以及孤立的线段数量，它也不难实现，但这时候问题来了，坐标的范围是-10000~10000,正常用这个坐标来更新线段树的话速度可能不够。所以最好的办法就是先对矩形边的x坐标离散化(不过本题中如果数据不太变态，不离散化估计也能过)

线段树的维护：这也是一个难点，越用这东西越觉得它有很多东西值得钻研。本题中要维护的2个线段树属性

1. 覆盖的总线段长
   
   因为对同个区域插入多次，他的总长度还是不变，对一个区域删除的次数要等于他插入的次数才能把区域中的长度减少，所以要在每个节点加上覆盖次数cover
2. 孤立线段的数量
   
   因为要判断2个子区域是否相连，加上bl,br记录当前节点左右边界是否被覆盖

时间复杂度\(O(n \log n)\)

#include<iostream>
#include<algorithm>
#define rg register
#define il inline
#define co const
template<class T>il T read(){
    rg T data=0,w=1;rg char ch=getchar();
    while(!isdigit(ch)) {if(ch=='-') w=-1;ch=getchar();}
    while(isdigit(ch)) data=data*10+ch-'0',ch=getchar();
    return data*w;
}
template<class T>il T read(rg T&x) {return x=read<T>();}
typedef long long ll;
using namespace std;

co int N=2e4+1,INF=0x3f3f3f3f;
int n,Max=-INF,Min=INF,tot,ans,pre;
struct P{
	int l,r,h,k;
	il bool operator<(co P&p)co {return h!=p.h?h<p.h:k>p.k;}
}a[N];
struct T{
	int sum,num,len;
	bool l,r;
}t[N*4];
il void add(int l,int r,int h,int k){
	a[++tot].l=l,a[tot].r=r,a[tot].h=h,a[tot].k=k;
}
#define lc (p<<1)
#define rc (p<<1|1)
il void work(int p,int l,int r){
	if(t[p].sum) t[p].num=t[p].l=t[p].r=1,t[p].len=r-l+1;
	else if(l==r) t[p].len=t[p].num=t[p].l=t[p].r=0;
	else{
		t[p].len=t[lc].len+t[rc].len;
		t[p].num=t[lc].num+t[rc].num;
		if(t[lc].r&&t[rc].l) --t[p].num;
		t[p].l=t[lc].l,t[p].r=t[rc].r;
	}
}
void change(int p,int l,int r,int L,int R,int k){
	if(L<=l&&r<=R) return t[p].sum+=k,work(p,l,r);
	int mid=l+r>>1;
	if(L<=mid) change(lc,l,mid,L,R,k);
	if(R>mid) change(rc,mid+1,r,L,R,k);
	work(p,l,r);
}
int main(){
//	freopen(".in","r",stdin),freopen(".out","w",stdout);
	read(n);
	for(int i=1,x1,y1,x2,y2;i<=n;++i){
		read(x1),read(y1),read(x2),read(y2);
		Max=max(Max,max(x1,x2)),Min=min(Min,min(x1,x2));
		add(x1,x2,y1,1),add(x1,x2,y2,-1);
	}
	if(Min<=0){
		for(int i=1;i<=tot;++i) a[i].l+=1-Min,a[i].r+=1-Min;
		Max-=Min; // len-1
	}
	sort(a+1,a+tot+1);
	for(int i=1;i<=tot;++i){
		change(1,1,Max,a[i].l,a[i].r-1,a[i].k);
		while(a[i].h==a[i+1].h&&a[i].k==a[i+1].k)
			++i,change(1,1,Max,a[i].l,a[i].r-1,a[i].k);
		ans+=abs(t[1].len-pre),pre=t[1].len;
		ans+=t[1].num*(a[i+1].h-a[i].h)*2;
	}
	printf("%d\n",ans);
	return 0;
}