P3378 【模板】堆 （内含左偏树实现）

P3378 【模板】堆

题解

其实就是一个小根堆啦，STL就可以解决，但是拥有闲情雅致的我学习了Jelly_Goat的左偏树，增加了代码长度，妙啊

Solution 1 STL

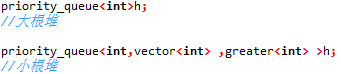
STL 里面priority_queue默认是大根堆，修改一下变成小根堆

#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<cstdlib>
#include<queue>

using namespace std;

typedef long long ll;

inline int read()
{
    int ans=;
    char last=' ',ch=getchar();
    while(ch<''||ch>'') last=ch,ch=getchar();
    while(ch>=''&&ch<='') ans=ans*+ch-'',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

int n,opr,x;
priority_queue<int,vector<int> ,greater<int> >h;

int main()
{
    n=read();
    while(n--)
    {
        opr=read();
        switch(opr)
        {
            case  : x=read();h.push(x);break;
            case  : printf("%d\n",h.top() );break;
            case  : h.pop() ;break;
            default : break ;
        }
    }
    return ;
}

Solution 2 左偏树

安利 Jelly_Goat 神仙的blog

什么是左偏树呢？

就是一个类似二叉堆的东西，画出来像一个二叉树

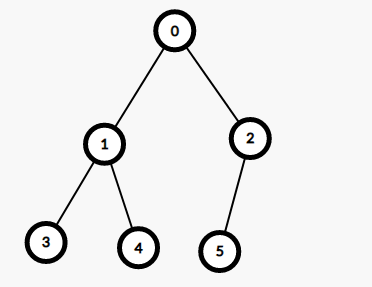
前置芝士：

1.我们定一个节点的 distance 为他距离自己子树中最右边节点的距离，下面简称 dist

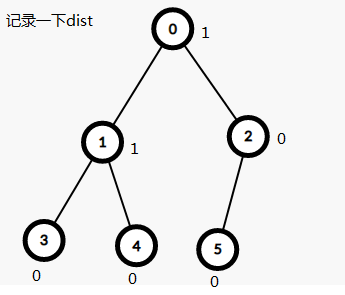
所以，没有右儿子的节点dist就是0啦

2.规定左偏树中，对于一个节点来说，他的左儿子的dist > 他的右儿子的dist

然后这棵树整体就左偏啦

3.怎么计算dist？？？

dfs跑一遍？？？

其实也就是 dist [ fa ] = dist [ rson ] + 1

因为得到一个节点的dist一定是与他的右儿子有关的，既然之前知道了右儿子的dist，从右儿子转移过来，也就是dist [ rson ] + 1 ，不就得到自己的dist了吗

支持操作

1.merge 合并操作

我们在用左偏树实现小根堆（大根堆也可以实现）

假设我们要合并两个小左偏树 a,b

（1）如果一个为空，直接返回另一个不就好啦

（2）如果两个都不为空，那么我们就把他们的根节点权值较小的一个作为合并后的根节点，如果两个根节点的权值一样，那么就把dist较大的一个作为新根节点

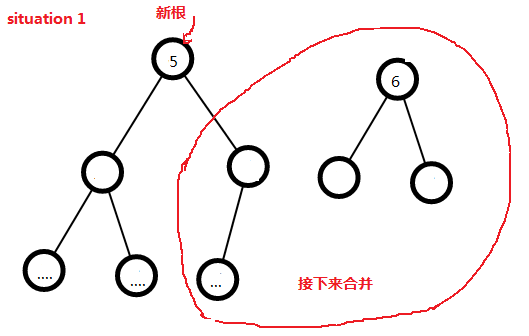
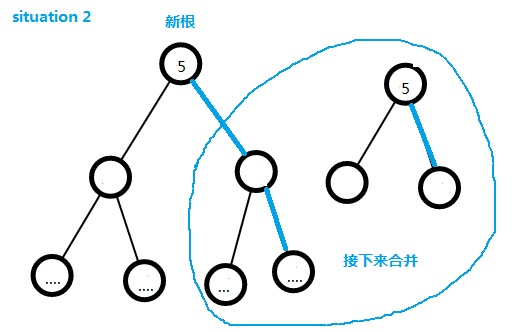
（3）然后继续往下面合并，假设新根是a，那么把b合并到他的右子树去，然后继续处理a的左右子树

（4）get一下新根的dist

2.insert 插入操作

get一个新的点，然后把他与原来的左偏树合并

3.top 访问堆顶 （左偏树实现小/大根堆）

如果堆不为空，就输出堆顶元素，否则输出0

4.pop 弹出堆顶

也就是把左偏树的根节点去掉，合并他的左右子树

5.size 记录一共多少个元素

int cnt 记录，每次新加一个点 就cnt++，弹出一个点，就cnt--

#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<cstdlib>
#include<queue>

using namespace std;

typedef long long ll;

inline int read()
{
    int ans=;
    char last=' ',ch=getchar();
    while(ch<''||ch>'') last=ch,ch=getchar();
    while(ch>=''&&ch<='') ans=ans*+ch-'',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

const int maxn=1e6+;

struct Heapnode
{
    int lson=,rson=,val=,dist=;
};

struct Heap
{
    Heapnode tree[maxn];
    int cnt=,tot=,rt=;
    inline int New(int val)
    {
        ++tot;
        tree[tot].val=val;
        return tot;
    }
    inline int set_dist(int a)
    {
        return tree[a].rson ? tree[tree[a].rson].dist+ : ;
    }
    int merge(int a,int b)
    {
        if(a==||b==) return a+b;
        else if(tree[a].val>tree[b].val) swap(a,b);
        else if(tree[a].val==tree[b].val&&tree[a].dist<tree[b].dist) swap(a,b);
        tree[a].rson=merge(tree[a].rson,b);
        if(tree[a].lson!=&&tree[a].rson!=){
            if(tree[tree[a].lson].dist<tree[tree[a].rson].dist)
               swap(tree[a].lson,tree[a].rson);
        }
        else if(tree[a].lson==&&tree[a].rson!=)
            swap(tree[a].lson,tree[b].rson);
        set_dist(a);
        return a;
    }
    inline void insert(int val)
    {
        cnt++;
        int b=New(val);
        rt=merge(rt,b);
    }
    inline int top()
    {
        return rt?tree[rt].val:;
    }
    inline void pop()
    {
        cnt--;
        int a=tree[rt].lson,b=tree[rt].rson;
        rt=merge(a,b);
    }
    inline int size()
    {
        return cnt;
    }
}h;

int n,opr,x;

int main()
{
    n=read();
    while(n--)
    {
        opr=read();
        switch(opr)
        {
            case  : x=read();h.insert(x);break;
            case  : printf("%d\n",h.top() );break;
            case  : h.pop() ;break;
            default : break ;
        }
    }
    return ;
}