bert系列一：《Attention is all you need》论文解读

论文创新点：

多头注意力
transformer模型

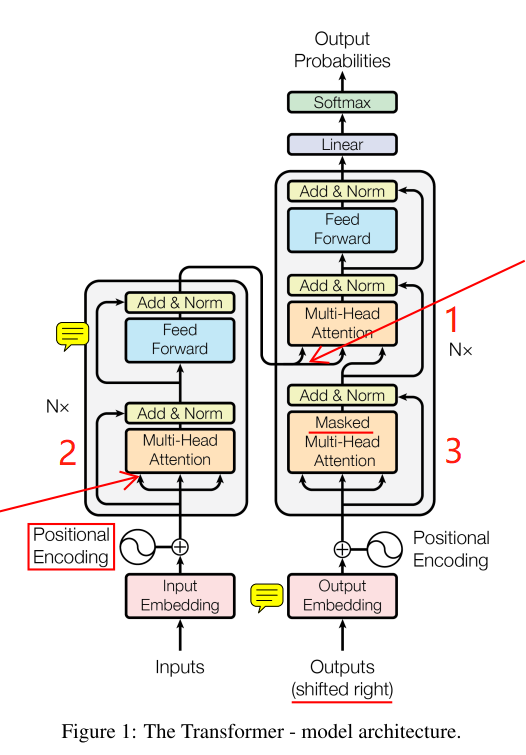
Transformer模型

上图为模型结构，左边为encoder，右边为decoder，各有N=6个相同的堆叠。

encoder

先对inputs进行Embedding，再将位置信息编码进去（cancat方式），位置编码如下：

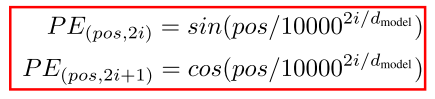
然后经过多头注意力模块后，与残余连接cancat后进行一个Norm操作，多头注意力模块如下：

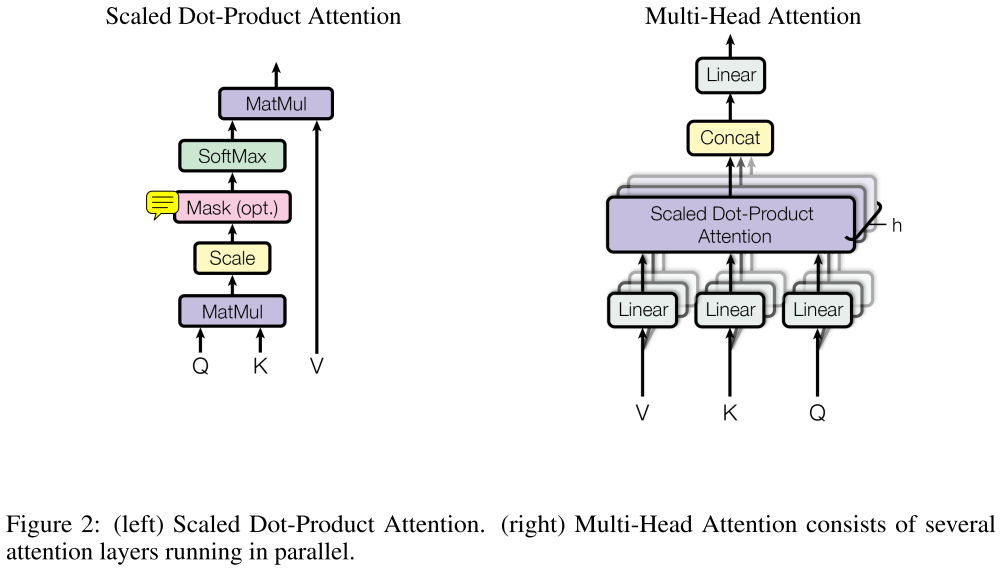
左图：缩放点乘注意力，这就是个平常的注意力机制，只不过多了scale和mask（仅对于decoder下面橙色框部分），使用的是dot-product attention，原文还提到另一种additive attention。

右图：多头注意力实现。每个Q，K，V都经过h个（不同）线性结构，以捕获不同子空间的信息，经过左图结构后，对h个dot-product attention进行concat后，再经过一个线性层。

之后，再通过一个有残余连接的前向网络。

decoder

同样先经过Embedding和位置编码，输入outputs右移了（因为每一个当前输出基于之前的输出）。

下面的橙色框：

之后也经过一个多头的self-attention，不同的是，它多了个mask操作。

这个mask操作是什么意思呢？注意我们的self-attention是一句话中每个词向量都与句子中所有词向量有关，对于encoder这没问题，而对于decoder，我们是根据之前的输出预测下一个输出。

举个例子，在BiLSTM中（当然这里是Transformer模型），假设我们decode时输入为A-B-C-D序列，在B处解码下一个输出时，我们根据之前的输出进行预测，但是这是双向模型，

即我们存在这样的一个之前的输出C-B-A-B，那么这个之前的输出里居然包含了我们下一个需要正确预测的C！这就是“自己看见自己”问题。

所以，mask操作是掩盖掉之后的位置（原文leftward，即向左流动的信息）的影响，原文是置为负无穷。这个橙色框我觉得可以称为half-self-attention。

最上面的橙色框：

它就不能叫self-attention结构了，因为它的K和V来自encoder的输出，Q是下面橙色框的输出。到这步为止，我们的输入inputs是完整的self-attention了，我们的输出outputs也是half-self-attention了。

好了，前戏准备完毕，开始短兵相接了。

这里的K和V一般相同，表示经过self-attention的隐藏语义向量，Q为经过half-self-attention的上一个输出，此处即为解码操作。经过一个有残余连接的前向网络，一个线性层，再softmax得到输出概率分布。

至此，Transformer模型描述完毕。

我们再看看self-attention模块，我之前一直不明白这些Q，K，V是啥东东。此处也是我个人推断。

在self-attention中，K，V表示当前位置的词向量，Q表示所有位置的词向量，用Q中每一个词向量与K进行操作（类似上面缩放点乘注意力截止到softmax），得到L个（L为句子单词数）权重向量。

此时应该有2种操作，一种是对L个权重向量相加，一种是取平均。得到的结果权重向量与V点乘，即为有self-attention后的词向量。

其余的实验及结果部分不再讲述，没什么难点。

这里再提下另一篇论文《End-To-End Memory Networks》中的一个模型结构。因为这篇论文被上面论文提到，对于理解上面论文有所帮助。

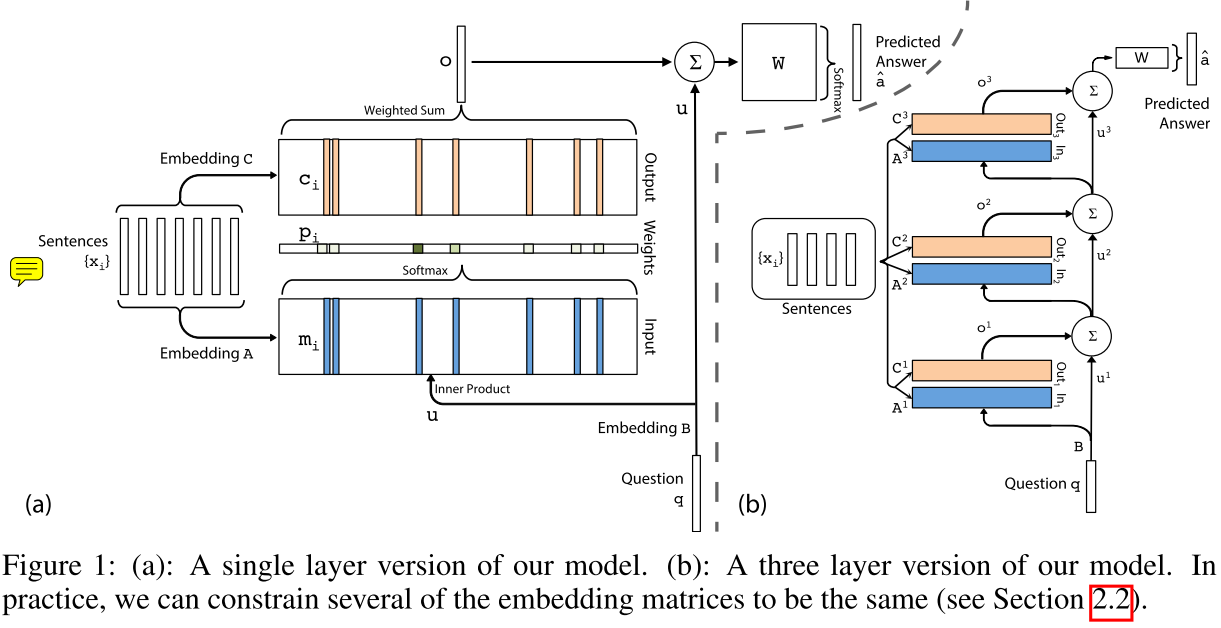
上图左边为单层，右边为多层版本。

单层的输出为：

Embedding B和C用于将输入x和问题q转化为嵌入向量，Embedding A用另一套参数将输出x转化为嵌入向量，与问题q共同决定注意力权重。

因为右图涉及到众多参数，为了简化模型，作者提出2种方案，这里直接上图：

这篇论文的创新点在于右图的多层版本类似RNNs，运算复杂度也比拟RNNs，避免了RNNs存在的一些问题。在QA问题上取得不错的成绩。