7.9模拟赛T1图的遍历（dfs）

图的遍历（dfs）

【题目描述】

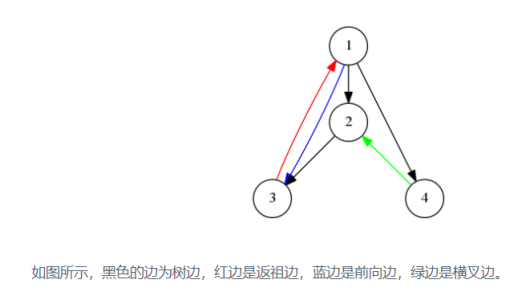
对于一个有向图G来说，我们存在一个经典的遍历算法，就是DFS （深度优先搜索遍历）。将G以1号点为起点进行DFS后，我们可以 得到G的一棵DFS遍历树T。就此，我们可以把G中的所有边分成4种 类型，如下： • 树边：边(u,v)满足是T上的边。 • 返祖边：边(u,v)满足在T上v是u的祖先。 • 前向边：边(u,v)满足在T上u是v的祖先，但不是父亲（即不是 树边）。 • 横叉边：除去以上所有情况的边就是横叉边。 现在我们给出四个整数A,B,C,D，要求构造图G，使得对G以1号点开 始进行DFS后，树边个数为A，返祖边个数为B，前向边个数为C，横 叉边个数为D。要求构造的G满足，联通（可以从1号点出发到达其他 所有点）、无重边、无自环，否则视为不合法。你只需要输出其中 任意一个解即可，我们会用spj判断你的解是否合法。

【输入格式】

仅一行，四个整数，表示 A,B,C,D。

【输出格式】

如果不存在解，输出-1。 如果有解，请现在第一行输出一个整数N，表示G的点数。 接下来N行，第i行先输出一个数Degreei，表示第i个点的出度； 接下来输出Degreei个数，描述i的所有出边。 注意不能存在重边和自环。 请注意，对于点i，在DFS过程中，我们会根据你输出的边的顺序， 依次进行拓展。

【样例输入】

3 1 1 1

【样例输出】

4

3 2 4 3

1 3

1 1

1 2

【数据范围】

本题一共 10 个测试点，每个测试点分值为 10 分。测试数据可分为 6 个部分，具体分值和说明如下： • 10% 的数据满足：0≤A,B,C,D≤5。 • 10% 的数据满足：D=0 • 10% 的数据满足：B=C=0。 • 20% 的数据满足：A≤100。 • 20% 的数据满足：A≤1000。 • 30% 的数据满足：A≤100000。 对于 100%的数据， 满足 0≤A,B,C,D≤100000。

sol:(题解)树边+前向边和返祖边数量是等价的，两者取最大即可称为 X 类 边，极端情况是链，共 N*(N-1)/2 条 但横叉边与上面俩是互斥的，称为 Y 类边，极端情况是菊花，共 (N-1)*(N-2)/2 条 考虑把菊花的一个叶子挪到某个叶子下面，发现 Y 类边少了一 条，X 类边多了一条。链类似 于是可以判断无解的情况，即 X 类边+Y 类边>N*(N-1)/2 yy 横叉边有点奇怪，考虑构造 X 类边刚好的方案，那么之后能 连得横叉边数量是最多的，一定满足 进一步观察，一个点能贡献 X 类边的数量之和它的深度有关，于 是直接先搞条链，最后一个点深度刚好卡好，接下来全都是深度为 1 的叶子即可 有其他构造方案的同学可以上来交流一下

自己yy的：说人话，应该已经知道链加菊花会是最优的，然后先在一条链上凑到max(A+C,B），剩下的搞成菊花

建边的时候dfs下去，注意一下顺序即可

#include <bits/stdc++.h>
using namespace std;
typedef int ll;
inline ll read()
{
    ll s=;
    bool f=;
    char ch=' ';
    while(!isdigit(ch))
    {
        f|=(ch=='-'); ch=getchar();
    }
    while(isdigit(ch))
    {
        s=(s<<)+(s<<)+(ch^); ch=getchar();
    }
    return (f)?(-s):(s);
}
#define R(x) x=read()
inline void write(ll x)
{
    if(x<)
    {
        putchar('-'); x=-x;
    }
    if(x<)
    {
        putchar(x+''); return;
    }
    write(x/);
    putchar((x%)+'');
    return;
}
#define W(x) write(x),putchar(' ')
#define Wl(x) write(x),putchar('\n')
const int N=;
int n,A,B,C,D,X,Y,Id[N],Top,Father[N],Lower[N];
//树边个数为A，返祖边个数为B，前向边个数为C，横叉边个数为D
vector<int>E[N],Ans[N];
inline void Link(int u,int v)
{
    E[u].push_back(v); Ans[u].push_back(v);
}
inline void dfs(int u)
{
    int i,j;
    for(i=;i<=E[u].size();i++)
    {
        int v=E[u][i-];
        Father[v]=u;
        if(C)
        {
            for(j=Father[u];j&&C;j=Father[j])
            {
                Ans[j].push_back(v); C--; if(!C) break;
            }
        }
        if(B)
        {
            for(j=u;j&&B;j=Father[j])
            {
                Ans[v].push_back(j); B--; if(!B) break;
            }
        }
        if(D)
        {
            for(j=;j<=*Lower;j++)
            {
                Ans[v].push_back(Lower[j]); D--; if(!D) break;
            }
        }
        dfs(v);
    }
    Lower[++*Lower]=u;
}
int main()
{
    freopen("dfs.in","r",stdin);
    freopen("dfs.out","w",stdout);
    int i,j,Sum;
    R(A); R(B); R(C); R(D);
    Sum=X=max(B,A+C); Y=D; n=A+;
    if((long long)(1LL*n*(n-)/)<(long long)(X+Y)) return puts("-1"),;
    Id[Top=]=;
    for(i=;i<=n;i++)
    {
        if(Sum>=Top++n-i)
        {
            Link(Id[Top++],i); Sum-=Top; Id[Top]=i;
        }
        else
        {
            int tmp=Sum-(n-i); Link(Id[tmp-],i); Sum-=tmp;
        }
    }
    dfs();
    Wl(n);
    for(i=;i<=n;i++)
    {
        W((int)Ans[i].size());
        for(j=;j<=Ans[i].size();j++) W(Ans[i][j-]);
        putchar('\n');
    }
    return ;
}
/*
input
3 1 1 1
output
4
3 2 4 3
1 3
1 1
1 2
*/