《University Calculus》-chape4-导数的应用-微分中值定理

罗尔定理：如果函数f(x)在[a,b]上连续并且在(a,b)处处可微，并且有f(a) = f(b)，则我们必然何以找到一个c∈(a,b),使得f’(c) = 0.

证明：我们从函数f(x)的最大值和最小值出发，它们只能在如下的几种情况取得。

(1)    端点a、b处。.

(2)    f’(x) = 0处，x∈(a,b)。

(3)    导数不存在处。

考虑到罗尔定理对函数的限制，我们可以直接排除(3)，一旦最大值或者最小值的情况是(2)，那么就找到了定理中所描述的c。那么现在还存在一种情况，即最大值和最小值都在情况(1)中取得，此时结合f(a)=f(b),我们可以断定它是常数函数，也是满足定理的。

Ex1：证明x^3 + 3x + 1 = 0只有一个实数解.

证明：考虑反证法，设函数f(x) = x^3 + 3x + 1，那么它至少有两个零点，这里记为x0,x1，显然f(x)是连续函数处处可微，在[x0,x1]上利用罗尔定理，我们能够得到存在f’(x3) = 0，但是事实情况是f’(x) = 3x^2 + 3 > 0恒成立，显然我们的假设与现实相悖，得证。

其实罗尔定理的主要功能是证明拉格朗日中值定理。

拉格朗日中值定理：设f(x)在[a,b]上连续，在(a,b)上可微，那么存在c∈(a,b),满足：

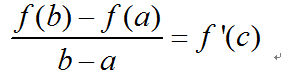
证明：

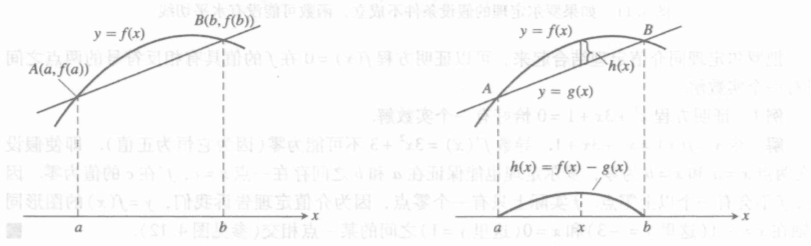
可以看到，罗尔定理是拉格朗日中值定理的一个特殊情况。

基于罗尔定理，我们将会推导出柯西中值定理，而柯西中值定理则是证明洛必达法则的重要工具。

柯西中值定理：

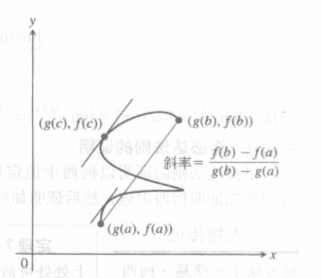
与拉格朗日的几何意义很类似，这里基于一个函数f、g的参数表达形式，我们能够给出柯西中值定理这样一个几何解释：

在x=f(t)，y=g(t)构成的图像当中，函数在a、b处两点形成的割线，在[a,b]之间必然存在一个c，使得x=c出的切线斜率等于割线的斜率。