最小费用流判负环消圈算法（poj2175）

Evacuation Plan

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 3384		Accepted: 888		Special Judge

Description

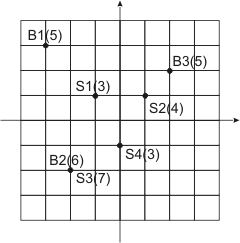The City has a number of municipal buildings and a number of fallout shelters that were build specially to hide municipal workers in case of a nuclear war. Each fallout shelter has a limited capacity
in terms of a number of people it can accommodate, and there's almost no excess capacity in The City's fallout shelters. Ideally, all workers from a given municipal building shall run to the nearest fallout shelter. However, this will lead to overcrowding
of some fallout shelters, while others will be half-empty at the same time. 



To address this problem, The City Council has developed a special evacuation plan. Instead of assigning every worker to a fallout shelter individually (which will be a huge amount of information to keep), they allocated fallout shelters to municipal buildings,
listing the number of workers from every building that shall use a given fallout shelter, and left the task of individual assignments to the buildings' management. The plan takes into account a number of workers in every building - all of them are assigned
to fallout shelters, and a limited capacity of each fallout shelter - every fallout shelter is assigned to no more workers then it can accommodate, though some fallout shelters may be not used completely. 



The City Council claims that their evacuation plan is optimal, in the sense that it minimizes the total time to reach fallout shelters for all workers in The City, which is the sum for all workers of the time to go from the worker's municipal building to the
fallout shelter assigned to this worker. 



The City Mayor, well known for his constant confrontation with The City Council, does not buy their claim and hires you as an independent consultant to verify the evacuation plan. Your task is to either ensure that the evacuation plan is indeed optimal, or
to prove otherwise by presenting another evacuation plan with the smaller total time to reach fallout shelters, thus clearly exposing The City Council's incompetence. 



During initial requirements gathering phase of your project, you have found that The City is represented by a rectangular grid. The location of municipal buildings and fallout shelters is specified by two integer numbers and the time to go between municipal
building at the location (Xi, Yi) and the fallout shelter at the location (Pj, Qj) is D_i,j = |Xi - Pj| + |Yi - Qj| + 1 minutes. 

Input

The input consists of The City description and the evacuation plan description. The first line of the input file consists of two numbers N and M separated by a space. N (1 ≤ N ≤ 100) is a number of municipal buildings in The City (all municipal buildings are
numbered from 1 to N). M (1 ≤ M ≤ 100) is a number of fallout shelters in The City (all fallout shelters are numbered from 1 to M). 



The following N lines describe municipal buildings. Each line contains there integer numbers Xi, Yi, and Bi separated by spaces, where Xi, Yi (-1000 ≤ Xi, Yi ≤ 1000) are the coordinates of the building, and Bi (1 ≤ Bi ≤ 1000) is the number of workers in this
building. 



The description of municipal buildings is followed by M lines that describe fallout shelters. Each line contains three integer numbers Pj, Qj, and Cj separated by spaces, where Pi, Qi (-1000 ≤ Pj, Qj ≤ 1000) are the coordinates of the fallout shelter, and Cj
(1 ≤ Cj ≤ 1000) is the capacity of this shelter. 



The description of The City Council's evacuation plan follows on the next N lines. Each line represents an evacuation plan for a single building (in the order they are given in The City description). The evacuation plan of ith municipal building consists of
M integer numbers E_i,j separated by spaces. E_i,j (0 ≤ E_i,j ≤ 1000) is a number of workers that shall evacuate from the i^th municipal building to the j^th fallout shelter. 



The plan in the input file is guaranteed to be valid. Namely, it calls for an evacuation of the exact number of workers that are actually working in any given municipal building according to The City description and does not exceed the capacity of any given
fallout shelter. 

Output

If The City Council's plan is optimal, then write to the output the single word OPTIMAL. Otherwise, write the word SUBOPTIMAL on the first line, followed by N lines that describe your plan in the same format as in the input file. Your plan need not be optimal
itself, but must be valid and better than The City Council's one.

Sample Input

3 4
-3 3 5
-2 -2 6
2 2 5
-1 1 3
1 1 4
-2 -2 7
0 -1 3
3 1 1 0
0 0 6 0
0 3 0 2

1 2
-1000 -1000 1000
999 0 600
0 1000 600
550 450

Sample Output

SUBOPTIMAL
3 0 1 1
0 0 6 0
0 4 0 1

SUBOPTIMAL
600 400

题意:一个城市中有n个大楼，m个避难所，接下来给出n个大楼的坐标和人数，接下来m行给出每个避难所的坐标和容纳量，大楼到避难所的距离定义为曼哈顿距离+1，然后给出n行m列数据，第i行第j列代表从第i个大楼到第j个避难所去的人数，保证此方案合法，然后判断此方案是否所有人到避难所的距离和最小，是的话输出OPTIMAL，否则给出更好的方案，但不一定是最优的；

分析：如果用最小费用最大流算法直接求解，会超时，此时有个更巧妙的算法，因为题目中已经给出了一套方案，然后就利用给出的方案建立残留网络图；建图方法如下：

第i个大楼到第j个避难所建立正向边，容量是inf-E[i][j]，费用是L[i][j]，然后建立反向边，容量是E[i][j]，费用是-L[i][j]；m个避难所到汇点分别建边，正向边容量是sht[j]-flow[j]，费用是0；反向边容量是flow[j]，费用是0；因为源点到大楼的流量全部流完，所以可以不用建立源点的图

判断是否有负环存在，从汇点入队开始搜，并且搜索边的容量不是0的边，每次更新的时候顺便更新记录当前点的上一个点保存到pre数组里面；判断完后，入队次数超过图中顶点个数的点不一定在负环当中，所以枚举每个点，利用pre回朔搜索看看是否会搜到被枚举的点，但搜到的话，用数组记录该环中的顶点

然后把i到j的边残余容量E+1，j到i的边残余容量E-1。

程序：

#include"stdio.h"
#include"queue"
#include"string.h"
#include"stdlib.h"
#include"vector"
#define inf 100000000
#define M 333
using namespace std;
int t,head[M],in[M],vis[M],dis[M],flow[M],pre[M],use[M];
struct Lode
{
    int x,y,val;
} but[M],sht[M];
int Fab(int a)
{
    if(a<0)
        a=-a;
    return a;
}
struct node
{
    int v,val,cost;
    node(int V,int VAL,int COST)
    {
        v=V;
        val=VAL;
        cost=COST;
    }
};
vector<node>edge[M];
int fuck[M],cnt;
int spfa(int s,int n)
{
    queue<int>q;
    memset(in,0,sizeof(in));
    memset(vis,0,sizeof(vis));
    memset(pre,-1,sizeof(pre));
    for(int i=0; i<=n; i++)
        dis[i]=inf;
    dis[s]=0;
    q.push(s);
    vis[s]=1;
    while(!q.empty())
    {
        int u=q.front();
        q.pop();
        vis[u]=0;
        for(int i=0; i<(int)edge[u].size(); i++)
        {
            int v=edge[u][i].v;
            if(edge[u][i].val&&dis[v]>dis[u]+edge[u][i].cost)
            {
                dis[v]=dis[u]+edge[u][i].cost;
                pre[v]=u;
                if(!vis[v])
                {
                    vis[v]=1;
                    q.push(v);
                    in[v]++;
                    if(in[v]>n)
                    {
                        return v;
                    }
                }
            }
        }
    }
    return 0;
}
int E[M][M],len[M][M];
int main()
{
    int n,m,i,j,k;
    while(scanf("%d%d",&n,&m)!=-1)
    {
        for(i=0; i<=n+m+1; i++)
            edge[i].clear();
        for(i=1; i<=n; i++)
            scanf("%d%d%d",&but[i].x,&but[i].y,&but[i].val);
        for(i=1; i<=m; i++)
            scanf("%d%d%d",&sht[i].x,&sht[i].y,&sht[i].val);
        for(i=1; i<=n; i++)
            for(j=1; j<=m; j++)
                len[i][j]=Fab(but[i].x-sht[j].x)+Fab(but[i].y-sht[j].y)+1;
        memset(flow,0,sizeof(flow));
        for(i=1; i<=n; i++)
        {
            for(j=1; j<=m; j++)
            {
                scanf("%d",&E[i][j]);
                edge[i].push_back(node(j+n,inf-E[i][j],len[i][j]));
                edge[j+n].push_back(node(i,E[i][j],-len[i][j]));
                flow[j]+=E[i][j];//到避难所的当前总流量
            }
        }
        for(j=1; j<=m; j++)
        {
            edge[j+n].push_back(node(n+m+1,sht[j].val-flow[j],0));
            edge[n+m+1].push_back(node(j+n,flow[j],0));
        }
        int ans=spfa(m+n+1,n+m+1);
        if(!ans)
        {
            printf("OPTIMAL\n");
            continue;
        }
        for(i=1; i<=m+n; i++)
        {
            memset(use,0,sizeof(use));
            use[i]=1;
            j=pre[i];
            int flag=0;
            while(j!=-1)
            {
                use[j]++;
                cnt=0;
                if(use[j]>=2)
                {
                    fuck[cnt++]=j;
                    k=pre[j];
                    while(k!=j&&k!=-1)
                    {
                        fuck[cnt++]=k;
                        k=pre[k];
                    }
                    fuck[cnt++]=k;
                }
                if(cnt)
                {
                    flag++;
                    break;
                }
                j=pre[j];
            }
            if(flag)break;
        }
        for(i=cnt-1; i>0; i--)
        {
            if(fuck[i]>=1&&fuck[i]<=n+m&&fuck[i-1]>=1&&fuck[i-1]<=m+n)
            {
                if(fuck[i]<=n&&fuck[i-1]>n)
                    E[fuck[i]][fuck[i-1]-n]++;
                if(fuck[i]>n&&fuck[i-1]<=n)
                    E[fuck[i-1]][fuck[i]-n]--;
            }
        }
        printf("SUBOPTIMAL\n");
        for(i=1; i<=n; i++)
        {
            for(j=1; j<=m; j++)
            {
                if(j==1)
                    printf("%d",E[i][j]);
                else
                    printf(" %d",E[i][j]);
            }
            printf("\n");
        }
    }
    return 0;
}