c/c++ 图的最短路径 Dijkstra(迪杰斯特拉)算法

c/c++ 图的最短路径 Dijkstra(迪杰斯特拉)算法

图的最短路径的概念：

一位旅客要从城市A到城市B，他希望选择一条途中中转次数最少的路线。假设途中每一站都需要换车，则这个问题反映到图上就是要找一条从顶点A到B所含边的数量最少的路径。我们只需从顶点A出发对图作广度优先遍历，一旦遇到顶点B就终止。由此所得广度优先生成树上，从根顶点A到顶点B的路径就是中转次数最少的路径。但是这只是一类最简单的图的最短路径问题。有时，对于旅客来说，可能更关心的是节省交通费用；而对于司机来说，里程和速度则是他们感兴趣的的信息。为了在图上表示相关信息，可对边赋以权值，权值可以表示两个城市之间的距离，或途中所需时间，或交通费用等等。此时路径长度的度量就不再是路径上边的数目，而是路径上边权值之和。

实现思路：

• 创建2个辅助int*数组dist path,1个bool数组s
• dist 存放目标顶点到每个顶点的最短距离
• path 存放目标顶点到每个顶点的路径
• s 被查找过的顶点设置为true，否则为false

图为下图

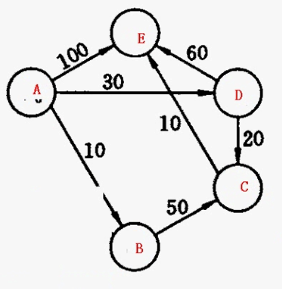
1，假设目标顶点为A，先从A开始找到各个顶点的权值,

	A	B	C	D	E
dist	0	10	无穷大	30	100
path	-1	0	0	0	0
s	true	false	false	false	false

path含义：比如path[1]=0,就代表从下标为0的顶点（A顶点）到B顶点

2，从dist里找到s为false的最小值，也就是dist[1]的值10，下标1说明是顶点B，再从B开始找到各个顶点的权值，更新dist和path，并设置B为true

	A	B	C	D	E
dist	0	10	60	30	100
path	-1	0	1	0	0
s	true	true	false	false	false

3,从dist里找到s为false最小值，也就是dist[3]的值30，下标3说明是顶点D，再从D开始找到各个顶点的权值，更新dist和path，并设置D为true

	A	B	C	D	E
dist	0	10	50	30	90
path	-1	0	3	0	3
s	true	true	false	true	false

4,从dist里找到s为false最小值，也就是dist[2]的值50，下标2说明是顶点C，再从C开始找到各个顶点的权值，更新dist和path，并设置C为true

	A	B	C	D	E
dist	0	10	50	30	60
path	-1	0	3	0	2
s	true	true	true	true	false

5,从dist里找到s为false最小值，也就是dist[4]的值60，下标4说明是顶点E，再从E开始找到各个顶点的权值，更新dist和path，并设置E为true

	A	B	C	D	E
dist	0	10	50	30	60
path	-1	0	3	0	2
s	true	true	true	true	true

下面两幅图可以帮助理解

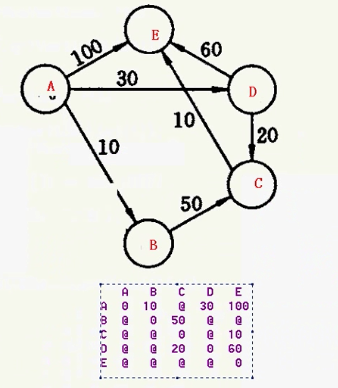
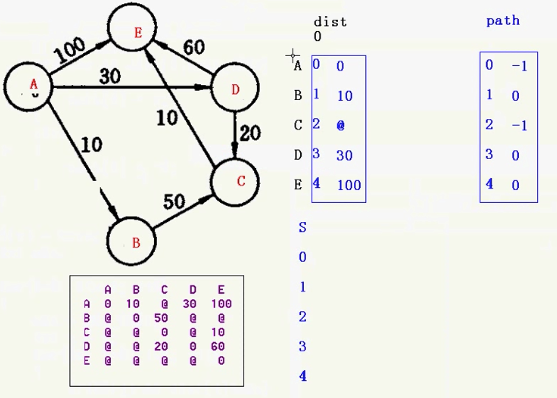
dijkstra.h

#ifndef __mixspantree__
#define __mixspantree__

#include <stdio.h>
#include <malloc.h>
#include <assert.h>
#include <memory.h>
#include <stdlib.h>
#include <stdbool.h>

#define Default_vertex_size 20

#define T char//dai biao ding dian de lei xing
#define E int
#define MAX_COST 0x7FFFFFFF

typedef struct GraphMtx{
  int MaxVertices;//zui da ding dian shu liang]
  int NumVertices;//shi ji ding dian shu liang
  int NumEdges;//bian de shu lian

  T* VerticesList;//ding dian list
  int** Edge;//bian de lian jie xin xi, bu shi 0 jiu shi 1
}GraphMtx;

//chu shi hua tu
void init_graph(GraphMtx* gm);
//打印二维数组
void show_graph(GraphMtx* gm);
//插入顶点
void insert_vertex(GraphMtx* gm, T v);
//添加顶点间的线
void insert_edge(GraphMtx* gm, T v1, T v2, E cost);

//最短路径
void short_path(GraphMtx* g,T v,E* dist, int* path);
#endif

dijkstra.c

#include "dijkstra.h"

void init_graph(GraphMtx* gm){
  gm->MaxVertices = Default_vertex_size;
  gm->NumEdges = gm->NumVertices = 0;

  //kai pi ding dian de nei cun kong jian
  gm->VerticesList = (T*)malloc(sizeof(T) * (gm->MaxVertices));
  assert(NULL != gm->VerticesList);

  //创建二维数组
  //让一个int的二级指针，指向一个有8个int一级指针的数组
  //开辟一个能存放gm->MaxVertices个int一级指针的内存空间
  gm->Edge = (int**)malloc(sizeof(int*) * (gm->MaxVertices));
  assert(NULL != gm->Edge);
  //开辟gm->MaxVertices组，能存放gm->MaxVertices个int的内存空间
  for(int i = 0; i < gm->MaxVertices; ++i){
    gm->Edge[i] = (int*)malloc(sizeof(int) * gm->MaxVertices);
  }
  //初始化二维数组
  //让每个顶点之间的边的关系都为不相连的
  for(int i = 0; i < gm->MaxVertices; ++i){
    for(int j = 0; j < gm->MaxVertices; ++j){
      if(i == j)
	gm->Edge[i][j] = 0;
      else
	gm->Edge[i][j] = MAX_COST;
    }
  }
}
//打印二维数组
void show_graph(GraphMtx* gm){
  printf("  ");
  for(int i = 0; i < gm->NumVertices; ++i){
    printf("%3c  ", gm->VerticesList[i]);
  }
  printf("\n");
  for(int i = 0; i < gm->NumVertices; ++i){
    //在行首,打印出顶点的名字
    printf("%c:", gm->VerticesList[i]);
    for(int j = 0; j < gm->NumVertices; ++j){
      if(gm->Edge[i][j] == MAX_COST){
	printf("%3c  ", '*');
      }
      else{
	printf("%3d  ", gm->Edge[i][j]);
      }
    }
    printf("\n");
  }
  printf("\n");
}
//插入顶点
void insert_vertex(GraphMtx* gm, T v){
  //顶点空间已满，不能再插入顶点了
  if(gm->NumVertices >= gm->MaxVertices){
    return;
  }
  gm->VerticesList[gm->NumVertices++] = v;
}

int getVertexIndex(GraphMtx* gm, T v){
  for(int i = 0; i < gm->NumVertices; ++i){
    if(gm->VerticesList[i] == v)return i;
  }
  return -1;
}
//添加顶点间的线
void insert_edge(GraphMtx* gm, T v1, T v2, E cost){
  if(v1 == v2)return;

  //查找2个顶点的下标
  int j = getVertexIndex(gm, v1);
  int k = getVertexIndex(gm, v2);
  //说明找到顶点了,并且点之间还没有线
  if(j != -1 && k != -1 ){
    //因为是有方向，所以更新1个值
    gm->Edge[j][k] = cost;
    //边数加一
    gm->NumEdges++;
  }
}

//取得2个顶点之间的权值
E getWeight(GraphMtx* g, int v1, int v2){
  if(v1 == -1 || v2 == -1) return MAX_COST;
  return g->Edge[v1][v2];
}
//最短路径
void short_path(GraphMtx* g,T v,E* dist, int* path){
  int n = g->NumVertices;
  bool* s = (bool*)malloc(sizeof(bool) * n);
  assert(NULL != s);

  int vi = getVertexIndex(g, v);
  for(int i = 0; i < n; ++i){
    //获得各个顶点与目标顶点之间的权值
    dist[i] = getWeight(g, vi, i);
    s[i] = false;
    if(i != vi && dist[i] < MAX_COST){
      path[i] = vi;
    }
    else{
      path[i] = -1;
    }
  }

  s[vi] = true;
  int min;
  int w;
  for(int i = 0; i < n - 1; ++i){
    min = MAX_COST;
    //u为最短路径顶点的下标
    int u = vi;
    for(int j = 0; j < n; ++j){
      if(!s[j] && dist[j] < min){
	u = j;
	min = dist[j];
      }
    }
    //把u加入到s集合
    s[u] = true;

    //更新下一个点到所有点的权值
    for(int k = 0; k < n; ++k){
      w = getWeight(g, u, k);
      if(!s[k] && w < MAX_COST && dist[u] + w < dist[k]){
	dist[k] = dist[u] + w;
	path[k] = u;
      }
    }
  }
}

dijkstramain.c

#include "dijkstra.h"

int main(){
  GraphMtx gm;
  //初始化图
  init_graph(&gm);
  //插入顶点
  insert_vertex(&gm, 'A');
  insert_vertex(&gm, 'B');
  insert_vertex(&gm, 'C');
  insert_vertex(&gm, 'D');
  insert_vertex(&gm, 'E');

  //添加连线
  insert_edge(&gm, 'A', 'B', 10);
  insert_edge(&gm, 'A', 'D', 30);
  insert_edge(&gm, 'A', 'E', 100);
  insert_edge(&gm, 'B', 'C', 50);
  insert_edge(&gm, 'C', 'E', 10);
  insert_edge(&gm, 'D', 'C', 20);
  insert_edge(&gm, 'D', 'E', 60);
  //打印图
  show_graph(&gm);

  int n = gm.NumVertices;
  E* dist = (E*)malloc(sizeof(E) * n);
  int* path = (int*)malloc(sizeof(int) * n);
  assert(NULL != dist && NULL != path);

  //最短路径
  short_path(&gm, 'A', dist, path);

}

完整代码

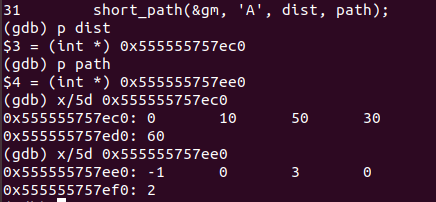
编译方法：gcc -g dijkstra.c dijkstramain.c

执行结果如下图：