nginx变量（日志log_format）

  • HTTP请求变量 - arg_PARAMETER、http_HEADER、sent_http_HEADER

它是指http请求中的变量，举例：

curl访问百度页面，需要在access.log显示Host字段内容

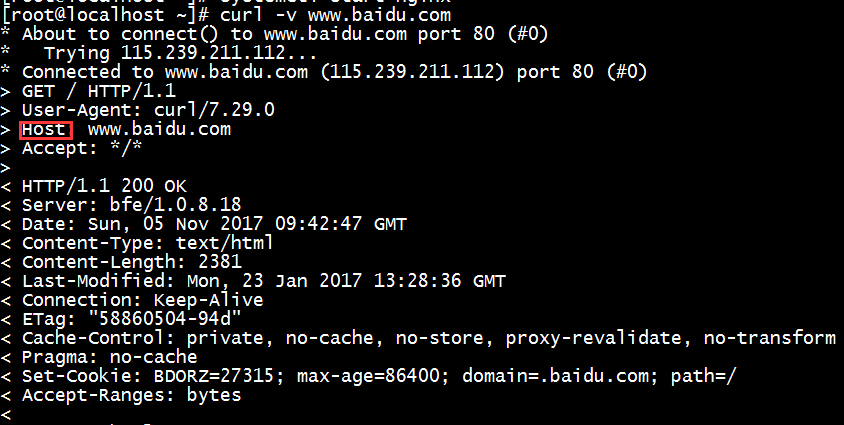
修改/etc/nginx/nginx.conf，配置内容等于http+请求包头名称

访问页面

  • 内置变量 - ngnix内置的

http://nginx.org/en/docs/http/ngx_http_log_module.html#log_format

  • 自定义变量 - 自己定义

nginx变量（日志log_format）的更多相关文章

  1. 《Nginx - 变量》- log_format/核心变量

    一:log_format - 概述 - log_format 用于管理 Nginx 的详细信息,日志管理等信息,很多都是基于这个来实现. - 可配置参数 $remote_addr 客户端地址 $rem ...

  2. nginx 日志log_format格式

    官方文档: http://nginx.org/en/docs/http/ngx_http_log_module.html The ngx_http_log_module module writes r ...

  3. log_format为Nginx设置日志格式

    nginx服务器日志相关指令主要有两条,一条是log_format,用来设置日志格式, 另外一条是access_log,用来指定日志文件的存放路径.格式和缓存大小,一般在nginx的配置文件中日记配置 ...

  4. 【nginx运维基础(4)】Nginx的日志管理(日志格式与定时分割日志)

    Nginx日志主要分为两种:访问日志和错误日志.日志开关在Nginx配置文件(一般在server段来配置)中设置,两种日志都可以选择性关闭,默认都是打开的. 访问日志access_log #日志格式设 ...

  5. nginx的日志配置

    本文转自:https://www.cnblogs.com/biglittleant/p/8979856.html 版权归属原作者!!!!!! nginx access日志配置 access_log日志 ...

  6. Nginx 错误日志配置

    1.Nginx错误日志信息介绍: error_log的语法格式及参数说明: error_log      file         level; 关键字    日志文件   错误日志级别 其中,关键字 ...

  7. Nginx 访问日志配置

    一.Nginx 访问日志介绍 Nginx 软件会把每个用户访问网站的日志信息记录到指定的日志文件里,供网站提供者分析用户的浏览行为等,此功能由 ngx_http_log_module 模块负责. 二. ...

  8. Nginx的日志剖析

    1.访问日志(access.log) Nginx的访问日志就是一个文件,它存储着每个用户对网站的访问请求,这个功能是有ngx_http_log_module模块来负责的,这个文件存在的主要目的就是为了 ...

  9. Nginx 访问日志

    配置访问日志: [root@localhost ~]$ cat /usr/local/nginx/conf/nginx.conf http { log_format main '$remote_add ...

随机推荐

  1. eolinker——分享项目只需两步

    登陆后打开项目概况 然后进入到分享项目界面,可根据自己的需求进行设置

  2. WEB请求处理

    https://blog.csdn.net/bpingchang/article/details/51328941

  3. prufer序列

    介绍 其实是\(pr\ddot{u}fer\)序列 什么是prufer序列? 我们认为度数为\(1\)的点是叶子节点 有一颗无根树,每次选出编号最小的叶子节点,加到当前prufer序列的后面,然后删掉 ...

  4. Java8的Stream语法详解（转载）

    1. Stream初体验 我们先来看看Java里面是怎么定义Stream的: A sequence of elements supporting sequential and parallel agg ...

  5. scrapy简单使用

    #settings.py文件设置 #如果网站中没有robots文件,就不会抓取任何数据 ROBOTSTXT_OBEY = False #设置请求头 DEFAULT_REQUEST_HEADERS = ...

  6. MT【169】拉格朗日配方

    已知$x^2+y^2+z^2=1$求$3xy-3yz+2z^2$的最大值______ 答案:$3$ 提示:$3(x^2+y^2+z^2)-(3xy-3yz+2z^2)=3\left(y+\dfrac{ ...

  7. python学习日记（函数--装饰器）

    楔子 前提,我有一段代码(一个函数). import time def run_time(): time.sleep(0.1) print('我曾踏足山巅') 需求1:现在,我想计算这段代码的运行时间 ...

  8. python学习日记（流程控制习题）

    请输出1-2+3...+99除88以外的和 i = 1 sum = 0 while i <= 99: if i == 88: i = i + 1 continue else: if i%2 == ...

  9. OpenLayers学习笔记（七）— 类似比例尺的距离环（一）

    openlayers 3 地图上创建一个距离环,始终以地图中心为中心,每个环之间的距离类似比例尺,随地图缩放而变化. 添加具有覆盖整个范围的特征的虚拟层,其可以被设置为围绕地图中心的环.注意,根据地图 ...

  10. Git错误汇总

    Git提示rejected To github.com:zhuxiaoxi/Web-Demo.git ! [rejected] master -> master (fetch first) er ...