C++解题报告 ： 迭代加深搜索之 ZOJ 1937 Addition Chains

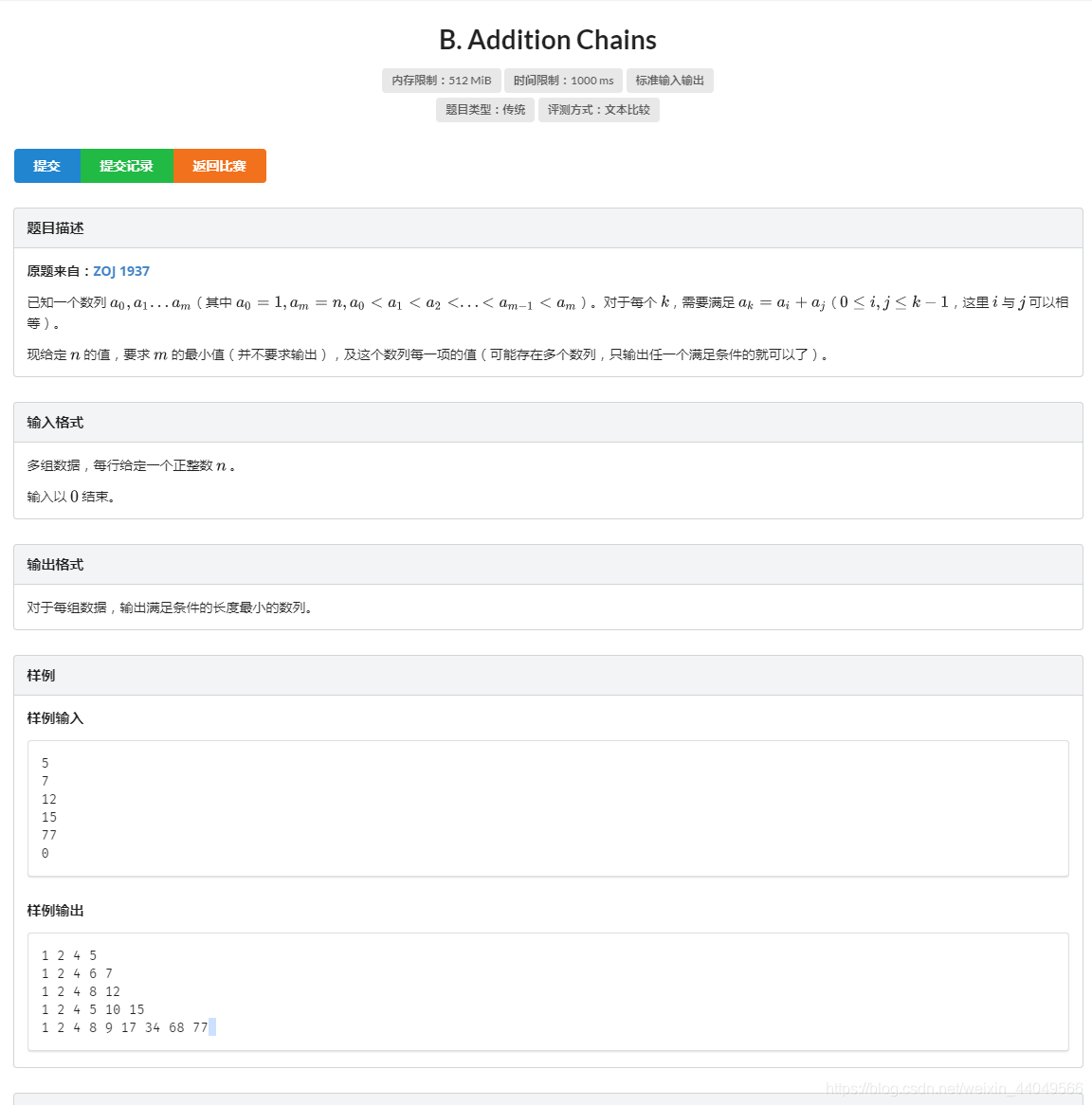
此题不难，主要思路便是IDDFS（迭代加深搜索），关键在于优化。

一个IDDFS的简单介绍，没有了解的同学可以看看：

https://www.cnblogs.com/MisakaMKT/articles/10767945.html

我们可以这么想，设当前规定长度为M，题目要求得出的数为N。

在搜索中，当前的步数为step,当前的数列为 数组a。

首先来确定思路，便是在以得出的数列a中枚举每两个数相加得出sum,然后继续搜索下一步。

初步的代码便是：

void iddfs(int step) {
	for(int i=1;i<=step；i++)
		for(int j=1;j<=step;j++) {
			a[step+1]=a[i]+a[j];
			iddfs(step+1);
		}
}

但是我们需要保证的数列应该是有序上升的，所以需要保证a[step+1]必须大于a[x]。

void iddfs(int step) {
	for(int i=1;i<=step；i++)
		for(int j=1;j<=step;j++) {
			a[step+1]=a[i]+a[j];
			if(a[step+1]>a[step]) continue;
			iddfs(step+1);
		}
}

但这样还不够，为了满足样例的需求，应该要从大到小来枚举加数。为了避免重复搜，还可以让j=i。

void iddfs(int step) {
	for(int i=step;i>=1；i--)
		for(int j=i;j>=1;j--) {
			a[step+1]=a[i]+a[j];
			if(a[step+1]<a[step]) continue;
			iddfs(step+1);
		}
}

现在可以发现可以简单的过样例了，但最后一个样例的时间却非常的长。所以我们应该要思考优化了。

可以发现序列的最后一个数最大都只能是\(a_{step}*2^{M-step}\)。为什么呢，因为要使最后结果最大，选的都必须是序列中最大的两个数，也就是最后一个数。结果算出来便就是\(a_{step}*2^{M-step}\)。

那么我们的优化就很简单了，如果\(a_{step}*2^{M-step}\)是小于N的，那就根本不可能有解，就需要舍去。这便是这道题剪枝的思想。

最后的代码：

#include <iostream>
#include <cstring>
using namespace std;

#define N 200

int a[200],n,len,flag;

void dfs(int step) {
	if(step>len) return ;
	if(step==len && a[step]==n) {//找到了解，输出
		for(int i=1;i<=step;i++)
			printf("%d ",a[i]);
		puts("");
		flag=1;
		return ;
	}
	if(a[step]>=n) return ;
	for(int i=step;i>=1;i--)
		for(int j=step;j>=i;j--) {
			if(a[i]+a[j]>a[step] && a[i]+a[j]<=n ) {
				a[step+1]=a[i]+a[j];
				int sum=a[i]+a[j];
                for(int k=step+2;k<=len;k++)
                    sum*=2;
                if(sum<n) continue;
				dfs(step+1);
				if(flag) return ;
			}
		}
}

int main() {
	while(cin>>n) {
		len=0;
		if( !n ) return 0;
		memset(a,0,sizeof(0));
		a[1]=1;a[2]=2,a[3]=4;
		int m=1;
		while(m<n) {//这句加不加都无所谓，对时间复杂度影响不大
			m*=2;//len完全可以从1开始
			len++;
		}
		for(len;;len++) {
			dfs(1);
			if(flag) break;
		}
		flag=0;
	}
}

include

include

using namespace std;

define N 200

int a[200],n,len,flag;

void dfs(int step) {

if(step>len) return ;

if(steplen && a[step]n) {

for(int i=1;i<=step;i++)

printf("%d ",a[i]);

puts("");

flag=1;

return ;

}

if(a[step]>=n) return ;

for(int i=step;i>=1;i--)

for(int j=step;j>=i;j--) {

if(a[i]+a[j]>a[step] && a[i]+a[j]<=n ) {

a[step+1]=a[i]+a[j];

int sum=a[i]+a[j];

for(int k=step+2;k<=len;k++)

sum*=2;

if(sum<n) continue;

dfs(step+1);

if(flag) return ;

}

}

}

int main() {

while(cin>>n) {

len=0;

if( !n ) return 0;

memset(a,0,sizeof(0));

a[1]=1;a[2]=2,a[3]=4;

int m=1;

while(m<n) {

m*=2;

len++;

}

for(len;;len++) {

dfs(1);

if(flag) break;

}

flag=0;

}

}