SciTech-EECS-BigDataAIML: SVD(奇异值分解) + Eigenvalue Decomposition(特征值分解)

SciTech-EECS-BigDataAIML:

SVD(奇异值分解)

Singular Value(奇异值) 就是 Eigenvalue 的平方根.

SVD 线性代数皇冠上的明珠

熟知SVD, 可以使我们更深刻地理解"Matrix(矩阵)"的"代数结构"和"几何意义".

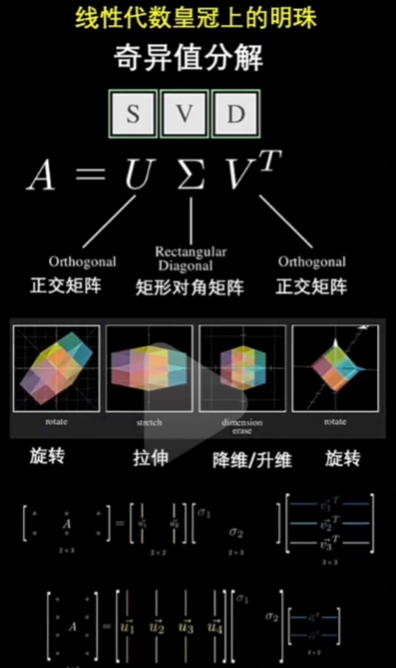
SVD(奇异值分解)不仅在科学、工程、机器学习 和 数据分析 等领域有非常重要的应用;

而且他把"Linear Algebra(线性代数)"的许多"核心概念"有机的联系在了一起. 例如:

• Rank: 秩
• Range: 像空间/列空间/范围
• Null Space: 零空间/核空间
• Eigenvalue: 特征值
• Eigenvector: 特征向量
• Transpose: 转置
• Inverse: 逆矩阵
• Symmetric Matrix: 对称矩阵
• Orthogonal Matrix: 正交矩阵
• PSD Matrix(Positive Semi Definite Matrix): 半正定矩阵

矩阵分解(矩阵因子分解)

矩阵分解(矩阵因子分解) 的一种方法, 即：

• 将 初始矩阵 表示成 “分解矩阵(两个或多个)”的乘积，
• 每个“分解矩阵”都是有 新结构 或 特殊性质的。类似于代数的因子分解

Eigenvalue Decomposition(特征值分解)

特征值分解 是 矩阵分解(矩阵因子分解) 的一种。

特征值分解的实质，是求解给定矩阵的 特征值和 特征向盘，提取出矩阵最重要的特征，

其中特征值分解公式 , 其中Q为特征向量矩阵， 是特征值对角阵。

• Eigenvalue Decomposition(特征值分解) 只适用于 的方阵 特征提取。

SVD(奇异值分解)

https://zhuanlan.zhihu.com/p/480389473

实际应用的数据对应的大部分矩阵可能不是方阵(如稀疏的有很多0), 就要提取主要特征；

• SVD(奇异值分解) 是将 任意较复杂矩阵 用 维度数更少, 更简单的“分解矩阵”的矩乘表示 ;
  
  例如可用 3个分解矩阵 来描述 “变换矩阵”(高维度的目标矩阵) 的重要特性。
• 矩阵\(A_{m \times n}\)不是方阵, 我们不能求其特征值;
• 但对于矩阵 \(A^T A\) 和 \(A A^T\)， 分别为\(n阶\)和\(m阶\)对称方阵:
  
  它们的秩等同: \(R(A^T A) = R(A A^T )=R(A)\), 而且它们的 非零特征值的集合 也等同,
• 对称矩阵 的 特征值矩阵 是 正交矩阵，特征值 都为 正实数; 因此可求出奇异值(特征值的平方根).

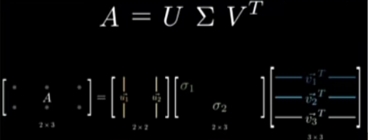
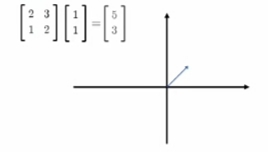
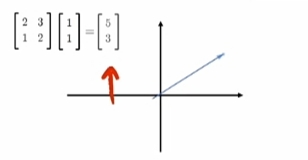
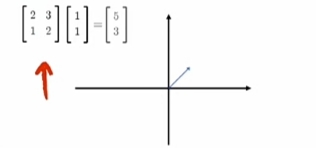
一个Matrix(矩阵)代表一个"线性变换"

• 一个矩阵代表一个“线性变换”
  
  

• 矩阵式线性变换：

  • 对一个vector(向量)/natrix(矩阵)“左乘”变换矩阵 就得到变换后的结果vector(向量)/natrix(矩阵).
    
    

  • 当“变换矩阵”是“方阵(行数=列数)”时, 变换不改变"作用向量"的shape(维度)；

    \[\large A_{m \times m} \times X_{m \times n} = Y_{m \times n}
    \]

• 变换的“规范化”::
  
  将“\(\large 变换矩阵A\)”规范化的分解成 三个 特殊类型的 分解变换矩阵:

  \[\large A_{m \times m} = U \sum V^{T}
  \]

• 变换的“维度变化”
  
  变换后的“结果矩阵”的“Rank(秩)”可能:

  • 同维: 等于 原vector(向量)/natrix(矩阵)的“Rank(秩)”：
  • 降维: 小于 原vector(向量)/natrix(矩阵)的“Rank(秩)”,将(\(\large Rank(X)-Rank(Y)\))个维度变换为"自由维度"；
    
    这种降维变换，可以只保留“Top K 特征值”对应Top K的“特征向量”;
    
    其实可看做: 其它(\(\large Rank(X)-Rank(Y)\))个“自由维度”的特征值为“0”(自由维度)；

• 对 "源矩阵"(\(\large X\)) 作"(\(\large A\))变换 得到 "终矩阵""(\(\large Y\)):
  
  每一个"向量/矩阵" 其实应当表示为“其本身”与“坐标基”的矩阵乘:
  
  (\(\large X = X \times I\)
  
  分解有两部分的变换:

  • 对 "空间单位(模长为1)坐标基"的变换, 旧"坐标基"为\(\large I\)，新"坐标基"的"每一维度"的模长为1；
  • 对 "向量新坐标值" 的变换: "源向量/矩阵" 投射到 新"坐标基"的"每一维度"上的"新坐标值(方向+模长)"的变换

SVD 应用实例 + 代码:

很多其它的机器学习算法也会用到SVD。使用线性代数时, 大多都要使用 SVD。SVD 不仅用在 PCA 、特征压缩(或数据降维)、图像压缩、数字水印、 推荐系统和文章分类、 LSA (隐性语义分析), 在信号分解/重构/降噪、数据融合、同标识别、目标跟踪、故障检测和神经网络等方面也有很好的应用.

矩阵压缩/降维

# -*- coding: utf-8 -*-
import numpy as np
from numpy import linalg as la
#1. SVD分解
A= [[1,1,3,6,1],[5,1,8,4,2],[7,9,2,1,2]]
A=np.array(A)
U,s,VT = la.svd(A)
# 为节省空间，svd输出s只有奇异值的向量
print('奇异值：',s)
# 根据奇异值向量s，生成奇异值矩阵
Sigma = np.zeros(np.shape(A))
Sigma[:len(s),:len(s)] = np.diag(s)

print("左奇异值矩阵：\n",U)
print('奇异值矩阵：\n',Sigma)
print('右奇异矩阵的转置：\n',VT)

#2.SVD重构
B = U.dot(Sigma.dot(VT))
print('重构后的矩阵B：\n', B)

print('原矩阵与重构矩阵是否相同？',np.allclose(A,B))

## 3. SVD矩阵压缩（降维）
for k in range(3,0,-1):  # 3,2,1
    # U的k列，VT的k行
    D = U[:,:k].dot(Sigma[:k,:k].dot(VT[:k,:]))
    print('k=',k,"压缩后的矩阵：\n",np.round(D,1))  # round取整数

• 代码一定要自己跑跑，SVD 得到的特征值的前两项较大，最后一项值较小;
• 取不同的k值, 分别对应于取 U的前 k列, 变成 k阶方阵，
• 取 前k行，对比利用 矩阵乘积得到的新矩阵 与原始矩阵 的情况，
• 对比结果, SVD 后 的 特征值 主要集中在前两个数上，即当 k取2时, 得到的新矩阵较近似; 大多数信息完好的. 因此，保留比较大的奇异值及特征向量，达到用较少数据量 达到较好的矩阵近似效果。

图像的数字化技术与矩阵的奇异值分解

将图形分解成象素的一个矩形的数阵，信息就可以用一个矩阵 $ A_r=(a_{ij})^{m \times n}$ 存储。

数字化图形存储量的压缩方法, 可用 矩阵的奇异值分解 和 矩阵范数 的近似。

对数字图像矩阵\(A_r\) 作 SVD(奇异值分解) , 压缩是取一个$ rank=k (k<r)$的矩阵 \(A_k\) 近似。

奇异值分解的展开形式

\[\large A_r = \sigma_1 u_1 v_{1}^{H} + \sigma_2 u_2 v_{2}^{H} + \cdots + \sigma_n u_n v_{r}^{H}
\]

\[\large A_k = \sigma_1 u_1 v_{1}^{H} + \sigma_2 u_2 v_{2}^{H} + \cdots + \sigma_n u_n v_{k}^{H}
\]

• 存储 \(A_k\) 只要存储\(k\)个奇异值, $ k个m维向量 u_i $ 和$ n维向量v_j \(的所有分量, 共计\)k(m+n+1)$个元素。
• 如果$ m=n=1000 \(, 存储原矩阵\)A_r$需要存储\(1000 \times 1000\)个pixel。
  
  矩阵 \(A_k\)取$ k=100 $时, 近似图象已非常清晰, 存储量仅 100(2000+1)=200100个pixel。
  
  和矩阵 \(A_r\) 比较，存储量减少了80%。

案例2--图像压缩

# -*- coding: utf-8 -*-
from itertools import count
from PIL import Image
import numpy as np

def img_compress(img,percent):
    U,s,VT=np.linalg.svd(img)
    Sigma = np.zeros(np.shape(img))
    Sigma[:len(s),:len(s)] = np.diag(s)
    # 根据压缩比 取k值

    # 方法1 # k是奇异值数值总和的百分比个数，（奇异值权重）
    count = (int)(sum(s))*percent
    k = -1
    curSum = 0
    while curSum <= count:
        k+=1
        curSum += s[k]

    # 方法2
    # k = (int)(percent*len(s)) # k是奇异值个数的百分比个数

    # 还原后的数据D
    D = U[:,:k].dot(Sigma[:k,:k].dot(VT[:k,:]))
    D[D<0] = 0
    D[D>255] = 255
    return np.rint(D).astype('uint8')

# 图像重建
def rebuild_img(filename,percent):
    img = Image.open(filename,'r')
    a = np.array(img)
    R0 = a[:,:,0]
    G0 = a[:,:,1]
    B0 = a[:,:,2]
    R = img_compress(R0,percent)
    G = img_compress(G0,percent)
    B = img_compress(B0,percent)
    re_img = np.stack((R,G,B),2)
    # 保存图片
    newfile = filename+str(percent*100)+'.jpg'
    Image.fromarray(re_img).save(newfile)
    img = Image.open(newfile)
    img.show()

rebuild_img('test.jpg',0.6)

代码一定要动手跑，对比结果