线性代数 A 的 LU 分解

我们本章的目的是对 \(A=LU\) 进行分析，我们以这种思路来看待高斯消元。

好现在还是从简单的开始。

首先，讲一下上一章中没讲完的内容——乘积的逆。

假设 \(A\) 和 \(B\) 均是可逆矩阵，即有：

\[A·A^{-1} = I = A^{-1}·A
\]

那 \(AB\) 的逆是什么？使用单独的逆相乘吗？是的。

用矩阵 \(A\) 的逆和 \(B\) 的逆相乘，什么顺序？反顺序相乘。因此有：

\[(AB)(B^{-1}A^{-1})=I
\]

所以 \(A^{-1}B^{-1}\) 就是我们所求的东西。这里可以把括号抹去，想怎么乘就怎么乘，因为括号可以移动，矩阵有乘法结合律。

首先应该把什么乘起来？\(B\) 乘以 \(B\) 的逆，乘积为单位矩阵；\(A\) 乘以 \(A\) 的逆得到单位矩阵。

关于为什么逆矩阵顺序要反过来，就相当于原来你先脱鞋子在脱袜子，他的逆动作就该是先穿鞋子，再穿袜子，而不是先穿鞋子再穿袜子（bushi。

回到刚才的例子，还要放到另一侧来检验：

\[B^{-1}A^{-1}AB=I
\]

由于下一章可能会涉及到转置，这里就做一个铺垫。

如果转置某可逆方阵，那么其转置的逆是什么？

首先，\(A\) 矩阵可逆：

\[AA^{-1}=I
\]

两侧同时转置，则就要涉及到矩阵转置了。转置单位矩阵会得到什么？还是单位矩阵对吧，不管怎么转置行和列，因为单位矩阵是对称的所以不会有变化。如果我对左边的乘积进行转置，这还是得改变两者的顺序。分别转置两个矩阵，然后以相反顺序相反顺序相乘。

注：矩阵 \(A\) 的转置记作 \(A^T\)

\[(A^{-1})^TA^T = I
\]

这个公式的推导可以说是一目了然，它也足以告诉我们答案了，什么是矩阵 \(A\) 的转置的逆？就是\((A^{-1})^T\) 。

然后我们惊奇的发现：

\[(A^{-1})^T = (A^T)^{-1}
\]

也就是说，转置和逆这两种运算，对于单个矩阵而言，顺序可以颠倒。好，这些就是我们将要用到的基础公式。

接下来，我们回到我们的主题 \(A\) 的 \(LU\) 分解。

我假设有一个矩阵 \(A\) 它是一个具有一切美好性质的矩阵。考虑 \(2 \times 2\) 的情况。

\[A=\begin{bmatrix}
2&1\\
8&7
\end{bmatrix}
\]

所以 \(E_{2,1}\) 是多少？

很显然，

\[U = \begin{bmatrix} 2&1\\0&3 \end{bmatrix}\,\,\,\,\,
E_{2,1} = \begin{bmatrix}
1&0\\-4&1
\end{bmatrix}
\]

有：

\[\quad \quad E_{2,1}·A = U
\\
\begin{bmatrix}
1&0\\-4&1
\end{bmatrix}
\begin{bmatrix}
2&1\\
8&7
\end{bmatrix}=\begin{bmatrix} 2&1\\0&3 \end{bmatrix}
\]

我们开始计算：

\[\begin{equation}
A = LU\\
\begin{bmatrix}
2&1\\
8&7
\end{bmatrix}=
L
\begin{bmatrix}
2&1\\
0&3
\end{bmatrix}
\end{equation}
\]

所以，这里的 \(L\) 是什么，它和 \(E_{2,1}\) 有什么关系？是逆。因为如果两边同时乘以 \(E_{2,1}\) 的逆 \(\dots\)

\[\begin{aligned}
E_{2,1}·A·(E_{2,1})^{-1}&=U·(E_{2,1})^{-1}\\
I·A&=U·(E_{2,1})^{-1}\\
A&=U·(E_{2,1})^{-1}\\
\therefore L&=(E_{2,1})^{-1}\\
\because (E_{2,1})^{-1}&=\begin{bmatrix}
1&0\\
4&1
\end{bmatrix}\\
\therefore L&=\begin{bmatrix}
1&0\\
4&1
\end{bmatrix}
\end{aligned}
\]

好，这是 \(2 \times 2\) 的情况。那么，\(L\) 代表什么？为什么用字母 \(L\) ?

\(U\) 代表上三角矩阵（\(Upper\)），\(L\) 表示下三角矩阵（\(Lower\)）。

可以看到，他的对角线上都是 \(1\) 因为对角线上都是主元，有时我们会把主元单独列出来：

\[\begin{aligned}
A&=LDU\\
\begin{bmatrix}
2&1\\
8&7
\end{bmatrix}&=
\begin{bmatrix}
1&0\\
4&1
\end{bmatrix}
\begin{bmatrix}
2&0\\
0&3
\end{bmatrix}
\begin{bmatrix}
1&\frac{1}{2}\\
0&1
\end{bmatrix}
\end{aligned}
\]

\(D\) 表示对角矩阵 （\(Diagonal\)）

下面不能只停留在 \(2 \times 2\) 了，这里的例子非常简单。

接下来考虑 \(3 \times 3\) 的情况：

\[\begin{aligned}
E_{3,2}E_{3,1}E_{2,1}A&=U \,\,\,\,\,(No\,\,Row\,\,Exchanges)\\
A&={E_{2,1}}^{-1}{E_{3,1}}^{-1}{E_{3,2}}^{-1}U\\
&=LU
\end{aligned}
\]

我们假设一下：

\[E_{3,2}=\begin{bmatrix}
1&0&0\\
0&1&0\\
0&-5&1\\
\end{bmatrix}
\quad
E_{2,1}=\begin{bmatrix}
1&0&0\\
-2&1&0\\
0&0&1\\
\end{bmatrix}
\]

有：

\[\begin{bmatrix}
1&0&0\\
0&1&0\\
0&-5&1\\
\end{bmatrix}
\begin{bmatrix}
1&0&0\\
-2&1&0\\
0&0&1\\
\end{bmatrix}=
\begin{bmatrix}
1&0&0\\
-2&1&0\\
10&-5&1\\
\end{bmatrix}=E \longleftrightarrow EA=U
\]

下面我要反顺序计算它的逆：

\[\begin{bmatrix}
1&0&0\\
2&1&0\\
0&0&1\\
\end{bmatrix}
\begin{bmatrix}
1&0&0\\
0&1&0\\
0&5&1\\
\end{bmatrix}=
\begin{bmatrix}
1&0&0\\
2&1&0\\
0&5&1\\
\end{bmatrix}=L \longleftrightarrow A=LU
\]

对于 \(A=LU\) 如果不存在行交换，消元乘数可以直接写入 \(L\) 中。

我们考虑一个问题，**一个 \(n \times n\) 的矩阵 \(A\) ，需要多少次操作？ **

令 \(n=100\) 假设矩阵中没有 \(0\) 。

第一步，

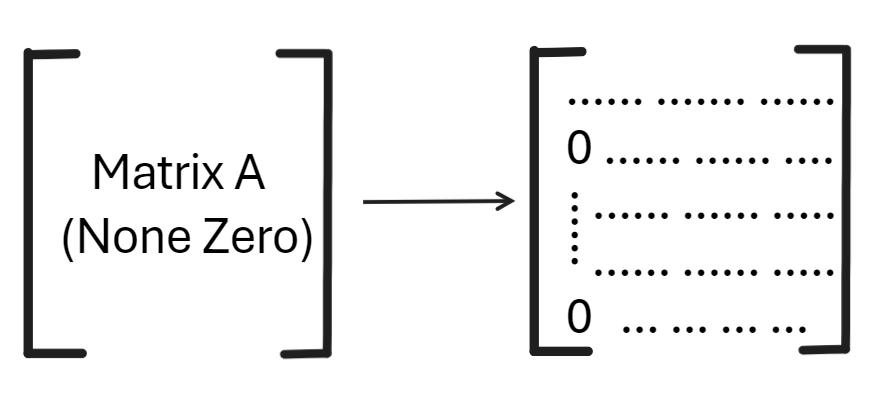
经过一步操作，剩下的就是 \(99 \times 99\) 的方阵了，因为主元已近在 \((1,1)\) 的位置，第一行已经固定，第一列同样的已经固定，剩下的也就是 \(99 \times 99\) 的方阵了。

那么，最终需要多少步？注意我们算的是时间复杂度（粗略理解就行，可能叫时间复杂度有点不太严谨），不是消元的次数。

所以，

\[Cost\,\,of\,\,A=n^2+(n-1)^2+(n-2)^2+\dots+1^2\approx\frac{1}{3}n^3\\
Cost\,\,of\,\,B=n^2
\]

下面讲讲置换（\(Permutations\)），考虑 \(3 \times 3\) 的情况。

有矩阵 \(\begin{bmatrix}
1&0&0\\
0&1&0\\
0&0&1
\end{bmatrix}\) ,通过一次置换可以得到： \(\begin{bmatrix}
0&1&0\\
1&0&0\\
0&0&1
\end{bmatrix}\) 、 \(\begin{bmatrix}
0&0&1\\
0&1&0\\
1&0&0
\end{bmatrix}\) 、

\(\begin{bmatrix}
1&0&0\\
0&0&1\\
0&1&0
\end{bmatrix}\) 、 \(\begin{bmatrix}
0&1&0\\
0&0&1\\
1&0&0
\end{bmatrix}\) 、 \(\begin{bmatrix}
0&0&1\\
1&0&0\\
0&1&0
\end{bmatrix}\) 。

仔细观察会发现这个矩阵群很有意思，将它们两两相乘，得到的矩阵仍然在这六个矩阵之中。

置换矩阵有一个很奇妙的性质：

\[P^{-1}=p^T
\]

它的逆等于其转置。我最后再讲一点，考虑 \(4 \times 4\) 的情况，有多少种转置矩阵？显然是 \(24\) 种。

本章到此结束。

预告：下一章的内容是转置和置换