Java八大排序之基数排序

基数排序（radix sort）属于“分配式排序”（distribution sort），又称“桶子法”（bucket sort）或bin sort，顾名思义，它是透过键值的部份资讯，将要排序的元素分配至某些“桶”中，藉以达到排序的作用，基数排序法是属于稳定性的排序，其时间复杂度为O (nlog(r)m)，其中r为所采取的基数，而m为堆数，在某些时候，基数排序法的效率高于其它的稳定性排序法。

步骤：

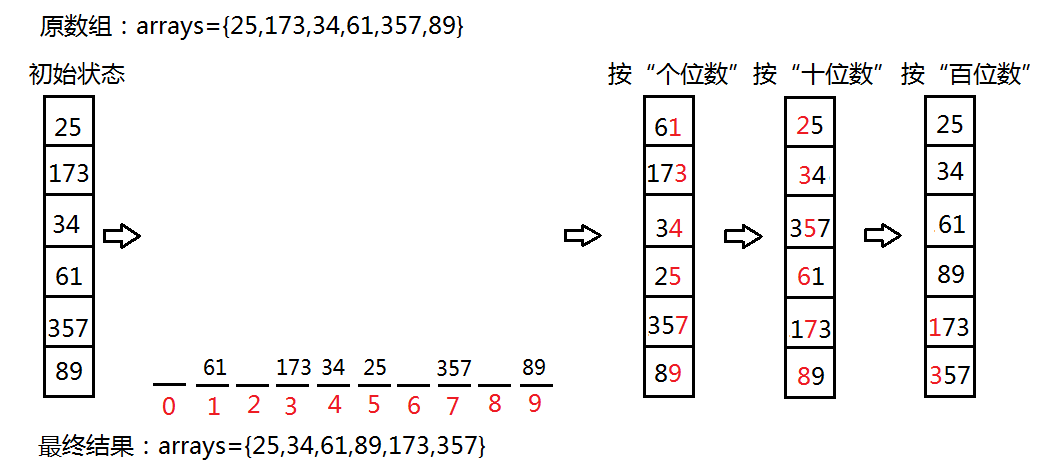
　　一，求出一个数组中最大的数的位数，表示要排序多少次；

　　二，先根据个位数排序，个位数相同的放入相同的桶子中，分别对应着0-9的桶子；

　　三，然后将桶子中的数据重新串连起来，按照0-9的桶子顺序和先进先出的规则；

　　四，重复第二步和第三步，只是之后的个位数分别设为十位数，百位数，千位数......，直到排序次数完结。

执行过程图：

代码：

 public class RadixSort {
     //最大数的位数
     public static int maxLength(int[] arrays){
         int maxArr = arrays[0];
         for (int i = 0; i < arrays.length-1; i++){
             if (arrays[i] < arrays[i+1]){
                 maxArr = arrays[i+1];
             }
         }
         return (maxArr+"").length();
     }
     //排序
     public static void radix(int[] arrays){
         int i = 0;
         int j;
         int n = 1;
         int index = 0;  //数组下标
         int l = arrays.length;  //数组长度
         int max = maxLength(arrays);    //最大数的位数
         //创建十个桶子数组
         int[][] tempArr = new int[10][l];
         //每个桶子的定义
         int[] counts = new int[10];
         while (i <= max){
             //把arrays数组中的数据分配到每个数组中
             for (j = 0; j < l; j++){
                 int temp = arrays[j]/n%10;
                 tempArr[temp][counts[temp]] = arrays[j];
                 counts[temp]++;
             }
             //将每个桶子数组中的数据收集到arrays数组中
             for (j = 0; j < counts.length; j++){
                 for (int a = 0; a < counts[j]; a++){
                     arrays[index] = tempArr[j][a];
                     index++;
                 }
                 counts[j] = 0;
             }
             index = 0;
             n = n*10;
             i++;
         }
     }
     //测试
     public static void main(String[] args) {
         int[] arrays={49,38,65,97,176,213,227,49,78,34,12,164,11,18,1};
         radix(arrays);
         System.out.println(Arrays.toString(arrays));
     }
 }

测试结果：

[1, 11, 12, 18, 34, 38, 49, 49, 65, 78, 97, 164, 176, 213, 227]

时间复杂度：设待排序列为n个记录，d为最大数的位数，radix为每个位数的取值范围。每次根据位数排序时，都会分为一趟收集和一趟分配，这个时间复杂度为O(n+radix);所以时间复杂度为O(d(n+radix))。

结语：优缺点还是不知道；