C++分治策略实现线性时间选择

问题描述：

给定线性序集中n个元素和一个整数k，1≤k≤n，要求找出这n个元素中第k小的元素，即如果将这n个元素依其线性序排列时，排在第k个的元素即为要找到元素。

细节须知：（与之前的随笔相比）

（1）设置了对于程序运行次数的手动输入设定

（2）取消了文件的读入，直接生成随机数进行排序查找

（3）扩大了随机数的范围、数组的可申请大小

（4）时间统计精确到了微秒级

（5）运行结束后一次性写入提升了程序稳定性，写入的数据可用于数据分析图表

算法原理：

将n个输入元素划分成⌈n/5⌉个组，每组5个元素，只可能有一个组不是5个元素。用任意一种排序算法，将每组中的元素排好序，并取出每组的中位数，共⌈n/5⌉个。递归调用算法Select来找出⌈n/5⌉个元素的中位数。如果⌈n/5⌉是偶数，就找它的两个中位数中较大的一个。以这个元素作为划分基准。以此递归排序找到所需的第k项。

 #include<iostream>
 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<fstream>
 #include<algorithm>
 #include<windows.h>
 #include<ctime>
 using namespace std;
 LARGE_INTEGER nFreq;//LARGE_INTEGER在64位系统中是LONGLONG，在32位系统中是高低两个32位的LONG，在windows.h中通过预编译宏作定义
 LARGE_INTEGER nBeginTime;//记录开始时的计数器的值
 LARGE_INTEGER nEndTime;//记录停止时的计数器的值
 
 //一次快排
 int Partition(int nums[],int p,int r,int x)
 {
     if(p>r) return -;
     //找出基准x的位置并与第一位交换
     for(int i=p;i<=r;i++)
     {
         if(nums[i]==x)
         {
             swap(x,nums[p]);
             break;
         }
     }
     int left=p,right=r;
     while(left<right)
     {
         while(left<right && nums[right]>=x) right--;
         nums[left]=nums[right];
         while(left<right && nums[left]<x) left++;
         nums[right]=nums[left];
     }
     nums[left]=x;
     return left;
 }
 
 //快速排序
 void QuickSort(int nums[],int low,int high)
 {
     if(low>high) return;
     int key=nums[low];
     int left=low,right=high;
     while(left<right)
     {
         while(left<right && nums[right]>=key) right--;
         nums[left]=nums[right];
         while(left<right && nums[left]<key) left++;
         nums[right]=nums[left];
     }
     nums[left]=key;
     QuickSort(nums,low,left-);
     QuickSort(nums,left+,high);
 }
 
 int Select(int nums[],int p,int r,int k)
 {
     if(r-p<)
     {
         QuickSort(nums,p,r);
         return nums[p+k-];
     }
     //每5个为一组，找到各组的中位数，并存储在前(r-p-4)/5个位置里
     for(int i=;i<=(r-p-)/;i++)
     {
         QuickSort(nums,p+*i,p+*i+);
         swap(nums[p+i],nums[p+*i+]);
     }
     //找所有中位数的中位数
     int x=Select(nums,p,p+(r-p-)/,(r-p-)/);
     //以x为基准做一次快排
     int i=Partition(nums,p,r,x);
     int j=i-p+;
     //判断k属于那个部分
     if(k<=j)
         return Select(nums,p,i,k);
     else
         return Select(nums,i+,r,k-j);
 }
 int main(){
     ofstream fout;
     double cost;
     int i = ,m = ,n = ,key = ;
     cout<<"Please enter the number of times you want to run the program:";        //输入程序运行次数
     cin>>m;
     int data_amount[m];
     double runtime[m];
     srand((unsigned int)time(NULL));      //设置随机数种子
     for(i=;i<m;i++)
     {
         n=+RAND_MAX*(rand()%)+rand();           //RAND_MAX=32767,随机生成数据量
         data_amount[i]=n;                               //限定数据规模为10000~9872867
         cout<<"☆The "<<i+<<"th test Data amount is："<<n<<endl;
         int j=;
         int *a=(int *)malloc(n*sizeof(int));
         for(j=;j<n;j++){
             a[j]=RAND_MAX*(rand()%)+rand();          //随机生成0~13139567的随机数
         }
         key=rand()%+;   //随机生成1~10000作为所要选择的次序
         QueryPerformanceFrequency(&nFreq);//获取系统时钟频率
         QueryPerformanceCounter(&nBeginTime);//获取开始时刻计数值
         int t=Select(a,,n-,key);
         QueryPerformanceCounter(&nEndTime);//获取停止时刻计数值
         cost=(double)(nEndTime.QuadPart - nBeginTime.QuadPart) / (double)nFreq.QuadPart;
         runtime[i]=cost;
         cout<<"The "<<key<<"th number is："<<t<<endl;
         cout<<"The running time is："<<cost<<" s"<<endl;
         free(a);
     }
     fout.open("data.txt");
     if(!fout){
         cerr<<"Can not open file 'data.txt' "<<endl;
         return -;
     }
     for(i=;i<m;i++){
            fout<<data_amount[i]<<","<<runtime[i]<<endl;
     }
     fout.close();
     cout<<"Success!"<<endl;
     return ;
 }

程序设计思路：

假设输入的数据规模为n，要查找的数据次序为k。

（1）判断数组长度，若小于75则直接进行快速排序，否则进行之后的算法。

（2）将n个输入元素划分成⌈n/5⌉个组，每组五个元素。用快速排序将每组中的元素排好序，并确定每组的中位数，共⌈n/5⌉个。

（3）递归调用算法Select来找出这⌈n/5⌉个元素的中位数。如果⌈n/5⌉是偶数，就找它的两个中位数中较大的一个。以这个元素作为划分基准。

（4）以此递归调用进行排序，最终搜索得到要找的第k项。

时间复杂性分析：

为了分析算法Select的计算时间复杂性，设n=r-p+1，即n为输入数组的长度。算法的递归调用只有在n≥75时才执行。因此，当n＜75是算法Select所用的计算时间不超过一个常数C₁。找到中位数的中位数x后，算法Select以x为划分基准调用Partition对数组a[p:r]进行划分，这需要O（n）时间。算法Select的for循环体行共执行n/5次，每一次需要O（1）时间。因此，执行for循环共需O（n）时间。

设对n个元素的数组调用算法Select需要T（n）时间，那么找中位数的中位数x至多用了T（n/5）的时间。已经证明了，按照算法所选的基准x进行划分所得到的2个子数组分别至多有3n/4个元素。所以，无论对哪一个子数组调用，Select都至多用了T（3n/4）的时间。

总之，可以得到关于T（n）的递归式

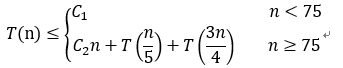
解此递归式可得T（n）=O（n）。

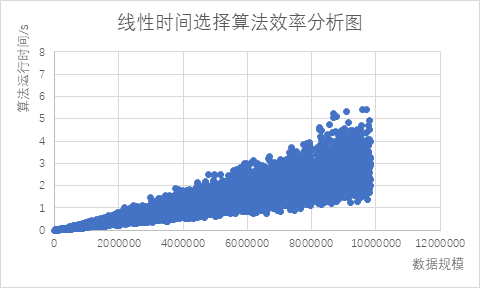
经过5000次不同规模数据的实验并统计运行时间得到如下算法效率分析图：