python算法与数据结构-双向链表(40)

一、双向链表的介绍

　　一种更复杂的链表是“双向链表”或“双面链表”。每个节点有两个链接：一个指向前一个节点，当此节点为第一个节点时，指向空值；而另一个指向下一个节点，当此节点为最后一个节点时，指向空值。

　　

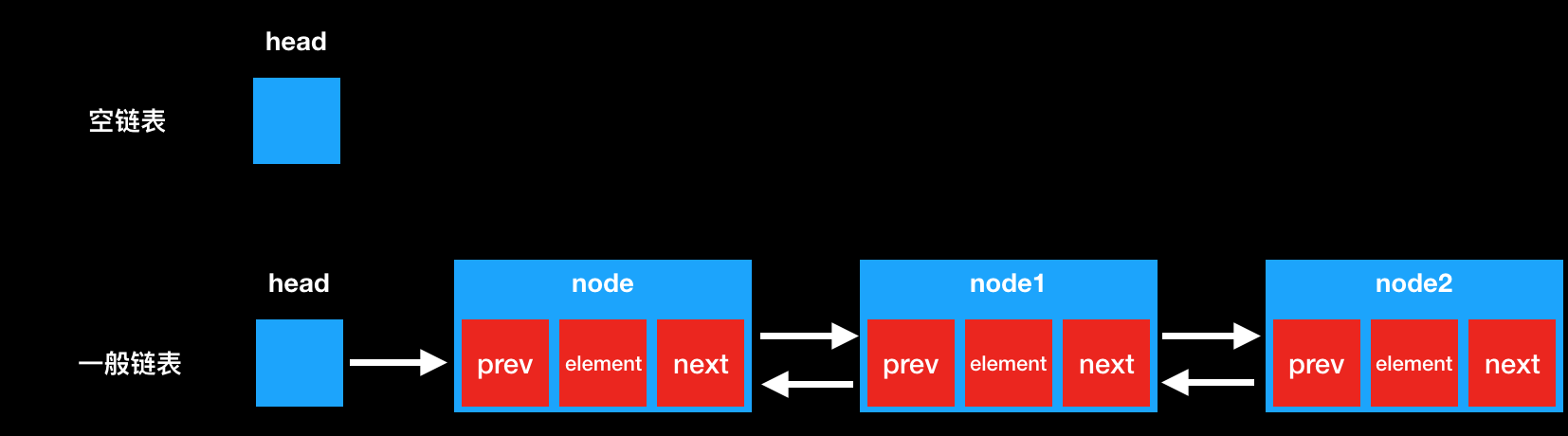
　　上图是双向链表的结构图，即通过上一个节点可以找到下一个，通过下一个也可以找到上一个节点。

二、双向链表插入和删除的图解

　　1、插入图解

　　

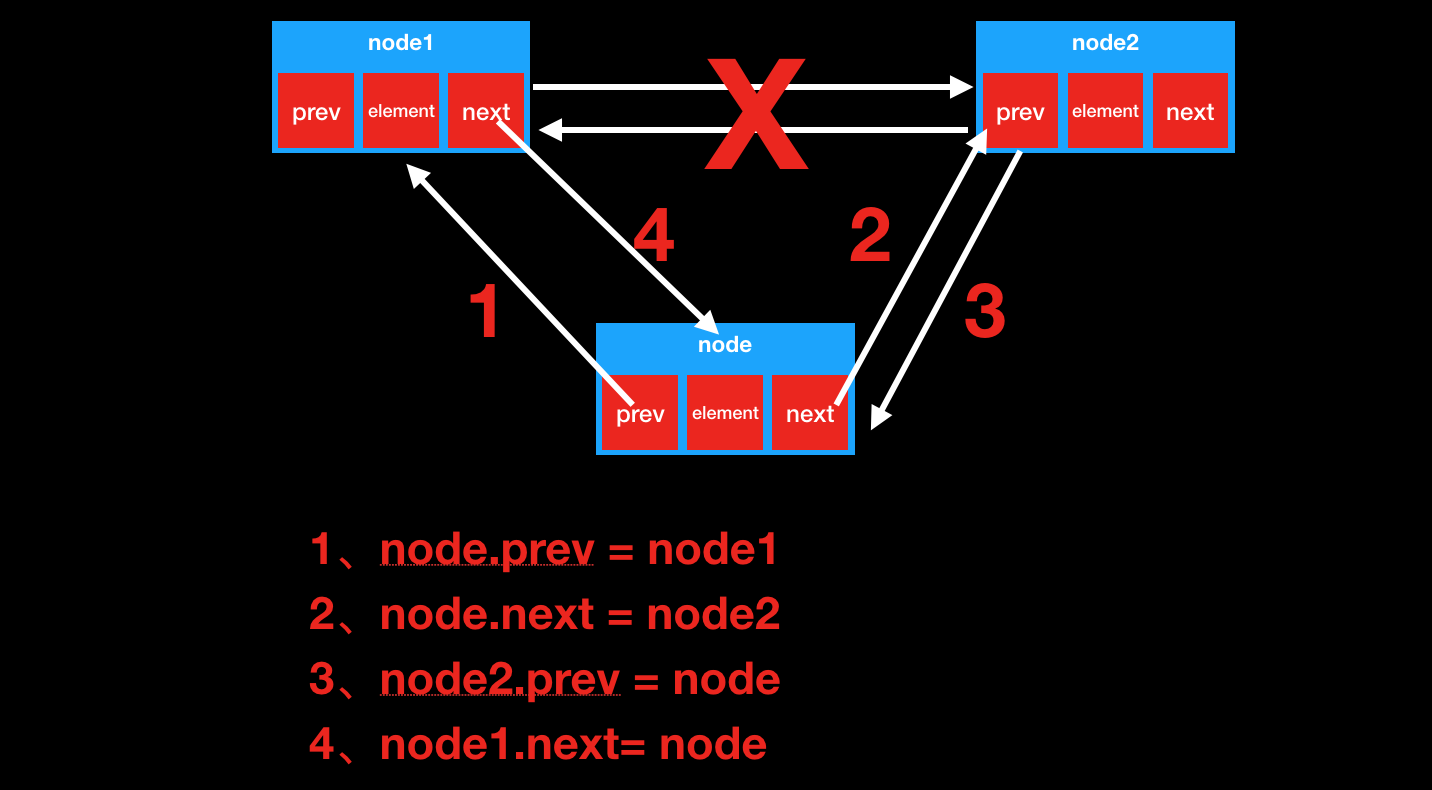
　　2、删除图解

　　

三、双向链表的python代码实现

# 1、创建节点
class Node(object):
    # 初始化方法
    def __init__(self, item):
        self.item= item
        self.next = None
        self.prev = None

# 2、创建循环链表
class DoubleLinKList(object):
    # 初始化方法
    def __init__(self):
        self._head = None

    # 3、判断是否为空
    def is_empty(self):
        """判断链表是否为空"""
        return self._head == None

    # 4、求其长度
    def length(self):
        """返回链表的长度"""
        cur = self._head
        count = 0
        while cur != None:
            count += 1
            cur = cur.next
        return count

    # 遍历
    def travel(self):
        """遍历链表"""
        print("你要遍历的链表元素有：",end=" ")
        cur = self._head
        while cur != None:
            print("%s "%cur.item,end=" ")
            cur = cur.next
        print("")

    # 5、头插
    def add(self, item):
        """头部插入元素"""
        node = Node(item)
        if self.is_empty():
            # 如果是空链表，将_head指向node
            self._head = node
        else:
            # 将node的next指向_head的头节点
            node.next = self._head
            # 将_head的头节点的prev指向node
            self._head.prev = node
            # 将_head 指向node
            self._head = node

    # 6、尾插
    def append(self, item):
        """尾部插入元素"""
        node = Node(item)
        if self.is_empty():
            # 如果是空链表，将_head指向node
            self._head = node
        else:
            # 移动到链表尾部
            cur = self._head
            while cur.next != None:
                cur = cur.next
            # 将尾节点cur的next指向node
            cur.next = node
            # 将node的prev指向cur
            node.prev = cur

    # 7、查找
    def search(self, item):
        """查找元素是否存在"""
        cur = self._head
        while cur != None:
            if cur.item == item:
                return True
            cur = cur.next
        return False

    # 8、指定位置插入
    def insert(self, pos, item):
        """在指定位置添加节点"""
        if pos <= 0 or pos>self.length()+1 :
            print("你输入的位置有误，请重新输入")
        elif pos == 1:
            self.add(item)
        elif pos == self.length()+1:
            self.append(item)
        else:
            node = Node(item)
            cur = self._head
            count = 1
            # 移动到指定位置的前一个位置
            while count < (pos - 1):
                count += 1
                cur = cur.next
            # 将node的prev指向cur
            node.prev = cur
            # 将node的next指向cur的下一个节点
            node.next = cur.next
            # 将cur的下一个节点的prev指向node
            cur.next.prev = node
            # 将cur的next指向node
            cur.next = node

    # 9、删除
    def remove(self, item):
        """删除元素"""
        if self.is_empty():
            return
        else:
            cur = self._head
            if cur.item == item:
                # 如果首节点的元素即是要删除的元素
                if cur.next == None:
                    # 如果链表只有这一个节点
                    self._head = None
                else:
                    # 将第二个节点的prev设置为None
                    cur.next.prev = None
                    # 将_head指向第二个节点
                    self._head = cur.next
                return
            while cur != None:
                if cur.item == item:
                    # 将cur的前一个节点的next指向cur的后一个节点
                    cur.prev.next = cur.next
                    # 将cur的后一个节点的prev指向cur的前一个节点
                    cur.next.prev = cur.prev
                    break
                cur = cur.next

# 验证
if __name__ == '__main__':

    double_link = DoubleLinKList()
    # 头插
    double_link.add(1)
    # 遍历
    double_link.travel()
    # 尾插
    double_link.append(2)
    double_link.travel()
    # 按照索引插入
    double_link.insert(3,4)
    double_link.travel()

    double_link.insert(3,3)
    double_link.travel()
    # 删除
    double_link.remove(3)
    double_link.travel()

运行结果为：

你要遍历的链表元素有： 1
你要遍历的链表元素有： 1  2
你要遍历的链表元素有： 1  2  4
你要遍历的链表元素有： 1  2  3  4
你要遍历的链表元素有： 1  2  4 

四、双向链表的C语言代码实现

//  main.m
//  双向链表
//  Created by 侯垒 on 2019/6/28.
//  Copyright © 2019 可爱的侯老师. All rights reserved.

#import <Foundation/Foundation.h>
typedef struct N
{
    int element;
    struct N *next;
    struct N *prev;
}Node;

// 创建节点
Node *createNode(int num)
{
    Node *node = (Node *)malloc(sizeof(Node));
    node->element = num;
    node->next = NULL;
    node->prev = NULL;
    return node;
}

// 创建双向链表
Node *createDoubleLinkList(Node *node)
{
    Node *head = node;
    return head;
}

// 判断是否为空
int is_empty(Node *head)
{
    if (head == NULL)
    {
        return ;
    }
    else
    {
        return ;
    }
}

// 求其长度
int length(Node *head)
{
    Node *current = head;
    int count = ;
    while (current != NULL)
    {
        count++;
        current = current->next;
    }
    return count;
}

// 遍历
void travel(Node *head)
{
    printf("你要遍历的数据有：");
    Node *current = head;
    while (current != NULL)
    {
        printf("%d ",current->element);
        current = current->next;
    }
    printf("\n");
}

// 头插
Node * add(Node *head,int num)
{
    Node *node = createNode(num);
    if (is_empty(head)==)
    {
        head = node;
    }
    else
    {
        node->next = head;
        head->prev = node;
        head = node;
    }
    return head;
}

// 尾插
Node* append(Node *head,int num)
{
    Node *node = createNode(num);
    if (is_empty(head)==)
    {
        head = node;
    }
    else
    {
        Node *current = head;
        while (current->next != NULL)
        {
            current = current->next;
        }
        current->next = node;
        node->prev = current;
    }
    return head;
}

// 查找
int search(Node *head,int num)
{
    Node *current = head;
    for (int i=; i<length(head); i++)
    {
        if (current->element == num)
        {
            return i+;
        }
        current = current->next;
    }
    return ;
}

// 按指定位置插入
Node * insert(Node *head ,int index,int num)
{
    if (index<=||index>length(head)+)
    {
        printf("你要插入的位置不对，请重新插入");
    }
    else if (index == )
    {
       head = add(head, num);
    }
    else if (index == length(head)+)
    {
        append(head, num);
    }
    else
    {
        Node *node = createNode(num);
        Node *current = head;
        for (int i=; i<index-; i++)
        {
            current = current->next;
        }
        node->prev = current;
        node->next = current->next;
        current->next->prev = node;
        current->next = node;
    }
    return head;
}

// 删除元素
Node * removeNode(Node *head,int num)
{
    if (is_empty(head)==)
    {
        printf("你要删除的链表为空");
    }
    else
    {
        Node *current = head;
        //处理头结点就是要删除的节点
        if (current->element == num)
        {
            if (current->next == NULL)
            {
                // 只有首节点这一个元素
                head = NULL;
            }
            else
            {
                // 要删除的是首节点，但是后面还有元素
                current->next->prev = NULL;
                head = current->next;
            }
        }
        else
        {
            while (current!=NULL)
            {
                if (current->element == num)
                {
                    current->prev->next = current->next;
                    current->next->prev = current->prev;
                    break;
                }
                current = current->next;
            }
        }
    }
    return head;
}

int main(int argc, const char * argv[]) {

    // 创建节点
    Node *node = createNode();
    // 创建链表
    Node *head = createDoubleLinkList(node);
    // 验证遍历
    travel(head);
    // 验证头插
    head = add(head, );
    travel(head);
    // 验证尾插
    head = append(head, );
    travel(head);

    // 验证查找
    int index = search(head, );
    if (index != )
    {
        printf("你要查找的数据在%d位置\n",index);
    }
    else
    {
        printf("没有找到你要的数据\n");
    }

    //验证按指定位置插入
    head = insert(head, , );
    travel(head);

    //验证删除
    head = removeNode(head, );
    travel(head);
    return ;
}

运行结果为：

你要遍历的数据有：
你要遍历的数据有：
你要遍历的数据有：
你要查找的数据在2位置
你要遍历的数据有：
你要遍历的数据有：