hdu 6198（矩阵快速幂）

number number number

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 175    Accepted Submission(s): 119

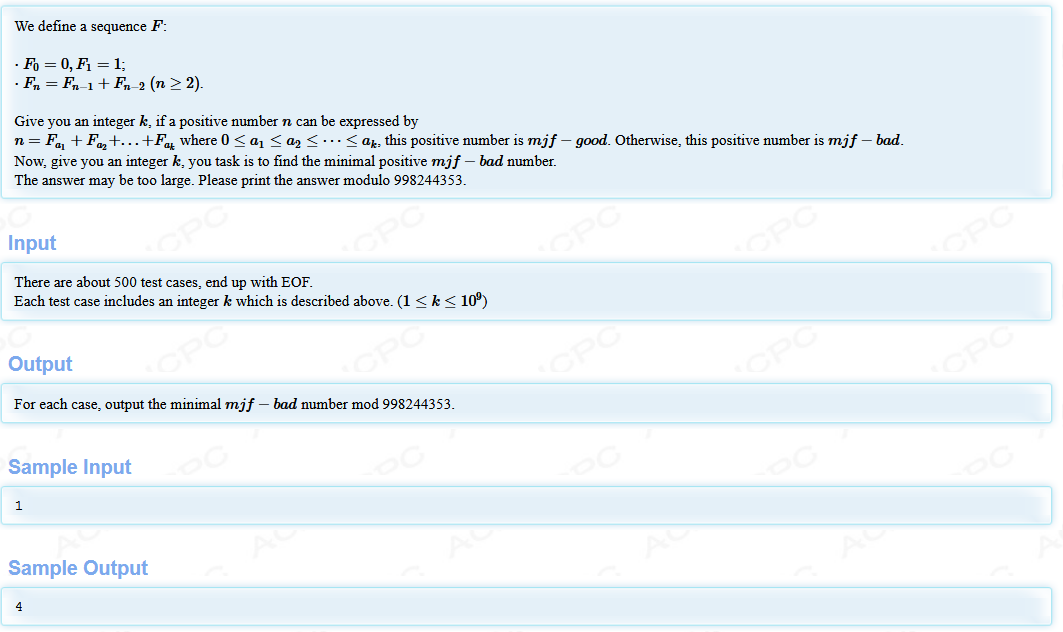
暴力发现当4 12 33 88 232

和斐波那契数列对比  答案为 第2*k+3个数减1

直接用矩阵快速幂求的F[2*k+3]  然后减1

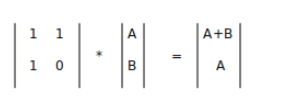A=1,B=0;

然后矩阵快速幂2*k+3-1次得到F[2*k+3]

 #include<iostream>
 #include<cstdio>
 #include<cmath>
 #include<cstring>
 #include<algorithm>
 #include<string.h>
 #include<map>
 #include<set>
 #include<queue>
 #include<vector>
 #include<cstdlib>
 typedef long long ll;
 typedef unsigned long long LL;
 using namespace std;
 const int INF=0x3f3f3f3f;
 const int num=;
 const int mod=;
 int N;
 struct Mat{
     ll a[num][num];
     void init(){
         memset(a,,sizeof(a));
         for(int i=;i<num;i++)
             a[i][i]=;
     }
 };
 Mat mul(Mat a,Mat b){
     Mat ans;
     for(int i=;i<N;i++){
     for(int j=;j<N;j++){
         ans.a[i][j]=;
         for(int k=;k<N;k++){
             ans.a[i][j]+=a.a[i][k]*b.a[k][j];
         }
         ans.a[i][j]=ans.a[i][j]%mod;
     }
     }
     return ans;
 }
 Mat power(Mat a,int n){
     Mat ans;
     ans.init();
     while(n){
         if(n&){
             ans=mul(ans,a);
         }
         n=n>>;
         a=mul(a,a);
     }
     return ans;
 }
 int main(){
     int k;
     N=;
     while(scanf("%d",&k)!=EOF){
         k=k*+;
         Mat aa;
         aa.a[][]=;
         aa.a[][]=;
         aa.a[][]=;
         aa.a[][]=;
         Mat ans=power(aa,k-);
         ll t=((ans.a[][]-)%mod+mod)%mod;
         cout<<t<<endl;
     }
     return ;
 }