ACM_平面、空间分割问题（递推dp）

折线分割平面

Time Limit: 2000/1000ms (Java/Others)

Problem Description:

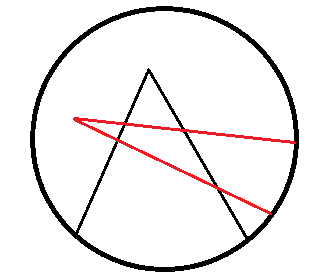
 我们看到过很多直线分割平面的题目，今天的这个题目稍微有些变化，我们要求的是n条折线分割平面的最大数目。比如，一条折线可以将平面分成两部分，两条折线最多可以将平面分成7部分，具体如下所示:

Input:

输入数据的第一行是一个整数C,表示测试实例的个数，然后是C 行数据，每行包含一个整数n(0<n<=10000),表示折线的数量。

Output:

对于每个测试实例，请输出平面的最大分割数，每个实例的输出占一行。

Sample Input:

3
1
2
12

Sample Output:

2
7
277
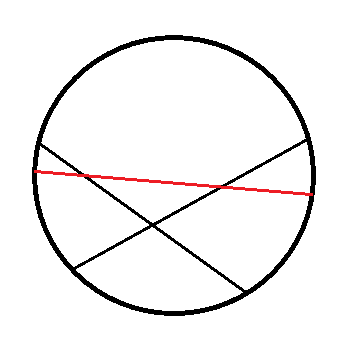
解题思路：首先来看看直线分割平面的情况：在一个平面上有一个圆和n条直线，这些直线中每一条在圆内同其他直线相交，假设没有3条直线相交于一点，试问这些直线将圆分成多少个区域。 

分析：当添加第n条直线时，为了使圆分割成更多的区域，第n条直线要与前n-1条直线都相交，且没有任何三条直线相较于一点，则添加第n条直线会多出n-1个交点。由于每增加n个交点，就会增加n+1个区域(比如原来圆中有2条直线、1个交点、4个区域，现多加了1条红色的直线，则多加了2个交点，共有3个交点，区域个数也多加了3个，一共把圆分成7个区域)，所以添加第n条直线会在原来的基础上增加n个区域。假设f(n)表示n条直线把圆内分成区域的个数，则易得递推式：f(n)=f(n-1)+n。
现在再来考虑折线分割平面的情况：平面上有n条折线，问这些折线最多能将平面分割成多少区域。

分析：由直线分割平面的结论可知，平面内原来直线与直线的交点个数决定了新增直线交点的个数，进而决定新增区域的个数。同理，当添加第n条折线时，为了使圆内分割成更多的区域，第n条折线的2条射线要与前n-1条折线相交，且没有三条射线相交于一点，则添加第n条折线会多出2*2(n-1)=4(n-1)个交点。由于每增加1个交点，就会增加2个区域，所以添加第n条折线会在原来的基础上增加4*(n-1)+1个区域。假设f(n)表示n条折线把圆内分成区域的个数，则易得递推式：f(n)=f(n-1)+4*(n-1)+1=f(n-1)+4*n-3。

AC代码：

 #include<bits/stdc++.h>
 using namespace std;
 int main()
 {
     int c,n,sum[]={,};//没有折线时只有一个平面块
     for(int i=2;i<;++i)
         sum[i]=sum[i-]+*i-;
     while(cin>>c){
         while(c--){
             cin>>n;
             cout<<sum[n]<<endl;
         }
     }
     return ;
 }

再来看看两道变形题：

M线分割平面（小数据）

Time Limit: 2000/1000ms (Java/Others)

Problem Description:

分割平面的题大家不会陌生了。
1条直线最多能把平面分割为2部分;
2条直线最多能把平面分割为4部分;
3条直线最多能把平面分割为7部分;
。。。等等。。。
这是用直线分割平面的，
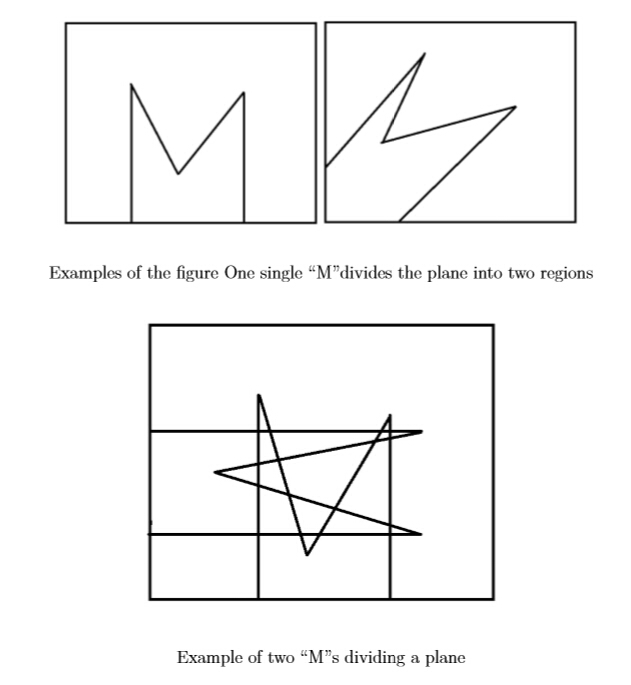
现在我们用M来分割平面。
如图所示例子。

Input:

输入首先输入一个整数T(1 ≤ T ≤ 1000)，接下来有T组数据，每组数据输入一个数N (0 ≤ N ≤ 10000),代表着M的个数。

Output:

对于每组数据，输出N个M最大能分割的平面数，格式参照样例输出。

Sample Input:

2
1
2

Sample Output:

Case #1: 2
Case #2: 19

解题思路：由上面的规律易得递推式：f(n)=f(n-1)+4*4(n-1)+1=f(n-1)+16*n-15。

AC代码：

 #include<bits/stdc++.h>
 using namespace std;
 int main(){
     int t,n,sum[]={,};
     for(int i=;i<;++i)
         sum[i]=sum[i-]+*i-;
     while(cin>>t){
         for(int i=;i<=t;++i){
             cin>>n;
             cout<<"Case #"<<i<<": "<<sum[n]<<endl;
         }
     }
     return ;
 }

N线分割平面

Time Limit: 2000/1000ms (Java/Others)

Problem Description:

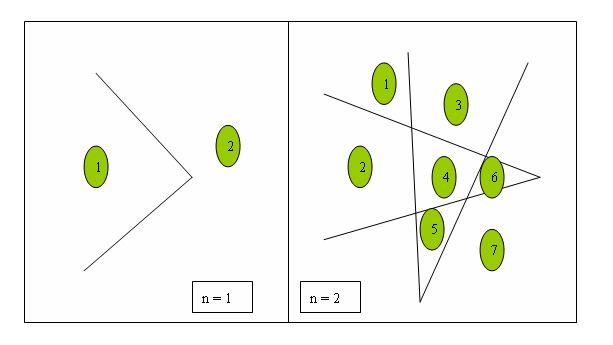
N型折线分割，如图，一个N型折线可以最多把平面分成2份，两个可以最多分成12份。那么n个N型折线可以最多把平面分成几份？

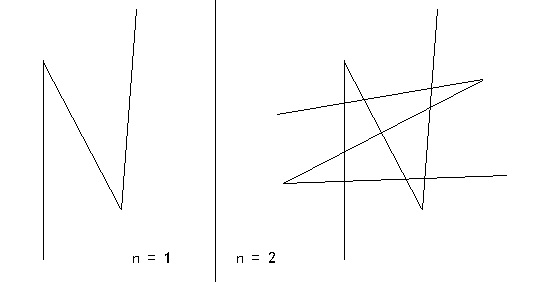
Input:

输入数据的第一行是一个整数C,表示测试实例的个数，然后是C 行数据，每行包含一个整数n(0<n<=10000),表示N型折线的数量。

Output:

对于每个测试实例，请输出平面的最大分割数，每个实例的输出占一行。

Sample Input:

2
1
2

Sample Output:

2
12

解题思路：由上面的规律易得递推式：f(n)=f(n-1)+3*3(n-1)+1=f(n-1)+9*n-8。

AC代码：

 #include<bits/stdc++.h>
 using namespace std;
 int main(){
     int c,n,sum[]={,};
     for(int i=;i<;++i)
         sum[i]=sum[i-]+*i-;
     while(cin>>c){
         while(c--){cin>>n;cout<<sum[n]<<endl;}
     }
     return ;
 }

以上规律只适用于不是封闭曲线（特定直线构成的图形）的所有情况。

接下来看看封闭曲线分割平面的情况：设有n条封闭曲线画在平面上，而任何两条封闭曲线恰好相交于两点，且任何三条封闭曲线不相交于同一点，问这些封闭曲线把平面分割成区域的个数。

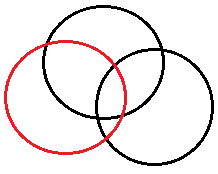
分析：先找找规律：当n=1时，封闭曲线上有0个交点，平面被分成了2个区域；当n=2时，为了使平面分成更多的区域，则第二条封闭曲线必须和前面1条曲线中每条曲线都有2个新的交点，一共就多出了2*1个新的交点，此时对应增加了2*1个区域，平面被分成了2+2=4个区域；当n=3时，同理且任何三条封闭曲线不相交于同一点，则第三条封闭曲线必须和前面2条曲线中每条曲线都有2个新的交点，一共就多出了2*2=4个新的交点，此时对应增加了4个区域，平面被分成了4+4=8个区域......由此可以推出当添加第n条封闭曲线时，其必须与前面n-1条曲线中每条曲线都有2个新的交点，一共就多出了2*(n-1) 个新的交点，此时对应增加了2*(n-1)个区域，所以添加第n条封闭曲线就会在原来的基础上多出2*(n-1)个区域。假设f(n)表示n条封闭曲线把平面分成区域的个数，则易得递推式：f(n)=f(n-1)+2*(n-1)。

实战：题解报告：hdu 1249 三角形

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1249

Problem Description

用N个三角形最多可以把平面分成几个区域?

Input

输入数据的第一行是一个正整数T(1<=T<=10000),表示测试数据的数量.然后是T组测试数据,每组测试数据只包含一个正整数N(1<=N<=10000).

Output

对于每组测试数据,请输出题目中要求的结果.

Sample Input

2

1

2

Sample Output

2

8

解题思路：结合以上的推导可知，当添加第n个三角形时，其必须与前面n-1个三角形中每个三角形都有2个新的交点，由于三角形有三条边，每条边与前面n-1个三角形都有2个新的交点，所以一共就会多出3*2(n-1)个新的交点，对应就会在原来的基础上增加6*(n-1)个区域。假设f(n)为n个三角形将平面分成区域的个数，则易得递推式：f(n)=f(n-1)+6*(n-1)。

AC代码：

 #include<bits/stdc++.h>
 using namespace std;
 int main(){
     int c,n,sum[]={,};
     for(int i=;i<;++i)
         sum[i]=sum[i-]+*(i-);
     while(cin>>c){
         while(c--){
             cin>>n;
             cout<<sum[n]<<endl;
         }
     }
     return ;
 }

最后讲讲平面分割空间的情况：由二维平面分割问题可以得出规律，交点的个数决定新增区域的个数，换一下思路，我们同样能在三维中找到递推式。当n=1时，空间中有0条交线，整个空间被分成2个区域；当n=2时，为了使空间分成更多的区域，则第2个平面必须与前面1个平面中每1个平面都有1条新的交线，此时第2个平面被分成2个区域，相应增加了2个空间区域，整个空间一共被分成2+2=4个区域；当n=3时，由于任何3个平面都不会相交于同一条直线，第3个平面必须与前面2个平面中每一个平面都有一条新的交线，并且此时第3个平面有2条相交直线将其分成4个区域，相应增加了4个空间区域，整个空间一共被分成4+4=8个区域......由此可以推出当添加第n个平面时，其必需与前面n-1个平面都有一条新的交线，且第n个平面有n-1条直线分割该平面，假设sum(n)表示n个平面将空间分成区域的个数，f(n)表示n条直线将平面分成区域的个数，则易得递推式sum(n)=sum(n-1)+f(n-1)，（其中f(n)=f(n-1)+n）。

实战：题解报告：hdu 1290 献给杭电五十周年校庆的礼物

Problem Description

或许你曾经牢骚满腹
或许你依然心怀忧伤
或许你近在咫尺
或许你我天各一方
对于每一个学子
母校 
永远航行在
生命的海洋
今年是我们杭电建校五十周年，这是一个值得祝福的日子。我们该送给母校一个怎样的礼物呢？对于目前的大家来说，最好的礼物当然是省赛中的好成绩，我不能参赛，就送给学校一个DOOM III球形大蛋糕吧，这可是名牌，估计要花掉我半年的银子呢。
想象着正式校庆那一天，校长亲自操刀，把这个大蛋糕分给各地赶来祝贺的校友们，大家一定很高兴，呵呵，流口水了吧...
等一等，吃蛋糕之前先考大家一个问题：如果校长大人在蛋糕上切了N刀（校长刀法极好，每一刀都是一个绝对的平面），最多可以把这个球形蛋糕切成几块呢？
做不出这个题目，没有蛋糕吃的！
为-了-母-校-，为-了-蛋-糕-（不是为了DGMM，枫之羽最会浮想联翩...），加-油-！

Input

输入数据包含多个测试实例，每个实例占一行，每行包含一个整数n(1<=n<=1000)，表示切的刀数。

Output

对于每组输入数据，请输出对应的蛋糕块数，每个测试实例输出一行。

Sample Input

1
2
3

Sample Output

2
4
8

解题思路：平面分割空间问题，直接套用上面的推导公式：sum(n)=sum(n-1)+f(n-1)。

AC代码：

 #include<bits/stdc++.h>
 using namespace std;
 int main(){
     int n,sum[]={,},f[]={,};
     for(int i=;i<;++i)
         sum[i]=sum[i-]+(f[i-]=f[i-]+i-);
     while(cin>>n){cout<<sum[n]<<endl;}
     return ;
 }