DQN(Deep Reiforcement Learning) 发展历程（三）

目录

• 不基于模型(Model-free)的预测
  • 蒙特卡罗方法
  • 时序差分方法
  • 多步的时序差分方法
• 参考

DQN发展历程(一)

DQN发展历程(二)

DQN发展历程(三)

DQN发展历程(四)

DQN发展历程(五)

不基于模型(Model-free)的预测

• 无法事先了解状态转移的概率矩阵

蒙特卡罗方法

• 从开始状态开始，到终结状态，找到一条完整的状态序列，以求解每个状态的值。相比于在整个的状态空间搜索，是一种采样的方法。

• 对于某一状态在同一状态序列中重复出现的，有以下两种方法：
  • 只选择第一个状态进行求解，忽略之后的所有相同状态
  • 考虑所有的状态，求平均值
• 对于求解每个状态的值，使用平均值代表状态值，根据大数定理，状态数足够多的条件下，该平均值等于状态值。平均值求解有两种方法：
  • 存储所有状态后求平均：消耗大量存储空间
  • 每次迭代状态都更新当前平均值：

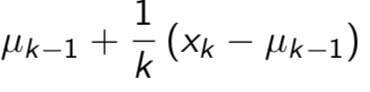
时序差分方法

• 蒙特卡罗方法需要获得从开始到终结的一条完整的状态序列，以求解每个状态的值，时序差分方法则不需要。根据贝尔曼不等式，只需要从当前状态到下一状态求解。
• 时序差分方法每步都更新状态值，而蒙特卡罗方法需要等到所有状态结束才更新。

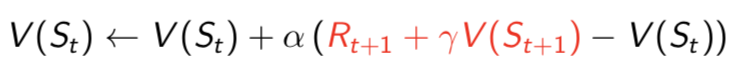
• 蒙特卡罗方法使用最后的目标来求解状态值，而时序差分使用下一状态的估计在每一步调整状态值。
• 蒙特卡罗方法是无偏估计方差较大，时序差分则是有篇估计但估计方差小。

多步的时序差分方法

• 时序差分方法使用当前状态值和下一状态值更新当前状态值，如果使用当前状态值和之后多步的状态值更新当前状态值，就是多步的时序差分方法。
• 当步数到最后的终结状态时，便是蒙特卡罗方法。
• 当步数到下一状态时，便是时序差分方法。
• 多步的时序差分方法，分为前向和后向的时序差分方法。

参考

david siver 课程

https://home.cnblogs.com/u/pinard/