UVALive 2218 Triathlon

https://vjudge.net/problem/UVALive-2218

题意：

铁人三项比赛，每项比赛长度未定，已知每个选手每项比赛的平均速度。

设计每项比赛的长度，让其中某个特定选手获胜。

判断哪些选手有可能 获得冠军，并列不算

每项比赛长度必须>0

线性规划问题

设比赛总长度为1，第一项长度为x，第二项长度为y，第三项长度为1-x-y

则选手i打败选手j的条件是

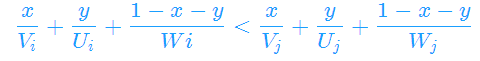
化为Ax+By+C>0，得

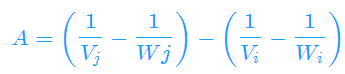
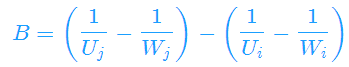
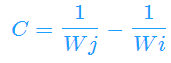
对于每个选手i，都会得到n-1个半平面

再加上x>0,y>0,1-x-y>0

一共n+2个半平面

如果这n+2个半平面有交，那么选手i可能获得冠军

#include<cmath>
#include<cstdio>
#include<algorithm>

#define N 104

using namespace std;

const double eps=1e-;

struct Point
{
    double x,y;

    Point(double x=,double y=) : x(x),y(y) { }

};

typedef Point Vector;

Vector operator + (Vector A,Vector B) { return Vector(A.x+B.x,A.y+B.y); }
Vector operator - (Vector A,Vector B) { return Vector(A.x-B.x,A.y-B.y); }
Vector operator * (Vector A,double b) { return Vector(A.x*b,A.y*b); }

struct Line
{
    Point P;
    Vector v;
    double ang;

    Line() {}
    Line(Point P,Vector v) :P(P),v(v) { ang=atan2(v.y,v.x); }

    bool operator < (Line L) const
    {
        return ang<L.ang;
    }
};

Line L[N];

double Cross(Vector A,Vector B)
{
    return A.x*B.y-A.y*B.x;
}

bool OnLeft(Line L,Point p)
{
    return Cross(L.v,p-L.P)>;
}

Point GetIntersection(Line a,Line b)
{
    Vector u=a.P-b.P;
    double t=Cross(b.v,u)/Cross(a.v,b.v);
    return a.P+a.v*t;
}

bool HalfplaneIntersection(Line *L,int n)
{
    sort(L,L+n);
    int first,last;
    Point *p=new Point[n];
    Line *q=new Line[n];
    q[first=last=]=L[];
    for(int i=;i<n;++i)
    {
        while(first<last && !OnLeft(L[i],p[last-])) last--;
        while(first<last && !OnLeft(L[i],p[first])) first++;
        q[++last]=L[i];
        if(fabs(Cross(q[last].v,q[last-].v))<eps)
        {
            last--;
            if(OnLeft(q[last],L[i].P)) q[last]=L[i];
        }
        if(first<last) p[last-]=GetIntersection(q[last-],q[last]);
    }
    while(first<last && !OnLeft(q[first],p[last-])) last--;
    return last-first>;
}

int V[N],U[N],W[N];

int main()
{
    int n;
    while(scanf("%d",&n)!=EOF)
    {
        for(int i=;i<n;++i) scanf("%d%d%d",&V[i],&U[i],&W[i]);
        for(int i=;i<n;++i)
        {
            int lc=; bool ok=true;
            double k=;
            for(int j=;j<n;++j)
                if(i!=j)
                {
                    if(V[i]<=V[j] && U[i]<=U[j] && W[i]<=W[j]) { ok=false; break; }
                    if(V[i]>=V[j] && U[i]>=U[j] && W[i]>=W[j]) continue;
                    double a=(k/V[j]-k/W[j])-(k/V[i]-k/W[i]);
                    double b=(k/U[j]-k/W[j])-(k/U[i]-k/W[i]);
                    double c=k/W[j]-k/W[i];
                    Point P;
                    Vector v(b,-a);
                    if(fabs(a)>fabs(b)) P=Point(-c/a,);
                    else P=Point(,-c/b);
                    L[lc++]=Line(P,v);
                }
            if(ok)
            {
                L[lc++]=Line(Point(,),Vector(,-));
                L[lc++]=Line(Point(,),Vector(,));
                L[lc++]=Line(Point(,),Vector(-,));
                if(!HalfplaneIntersection(L,lc)) ok=false;
            }
            puts(ok ? "Yes" : "No");
        }
    }
}