Linear Algebra lecture7 note
Computing the nullspace (Ax=0)
Pivot variables-free variables
Special solutions: rref( A)=R

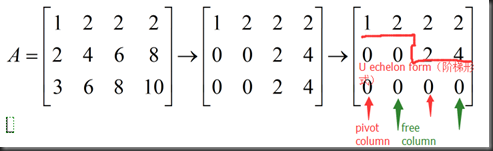
rank of A=the number of pivots=2
由上述矩阵行变换回代可得方程
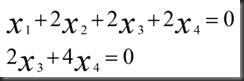
我们自行给free variable对应的x赋值
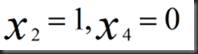
得到一个特解x为
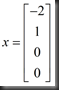 表示的意思是
表示的意思是
再赋一组值
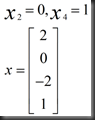 表示的意思是
表示的意思是
以上特解可以组成通解
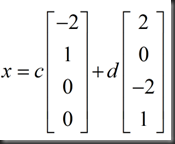
Reduce row(echelon form:zeros above and below pivots) 行最简形

rref (A) means (reduced row echelon form of A)
There are some information that this kind of form tells:
1.pivot rows are row1 and row2
2.pivot cols are col1 and col3
3.this matrix conclude an I(Identity) in it , made by pivot rows and pivot cols
4.全0行表示原行是其他行的线性组合
5.可得知自由列
6.回代得到特解
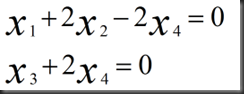
即我们由AX=0到UX=0,最终得到RX=0
交换R中各列,可得如下形式

rref form:
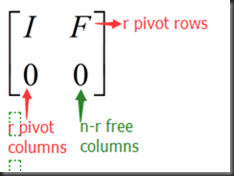
假设N是RX=0的一个特解

回代:
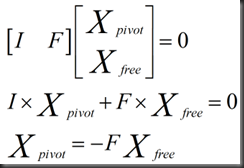
若Xfree赋值单位矩阵I,那么Xpivot可得到-F
特解与F有关,方程得以解出
example:
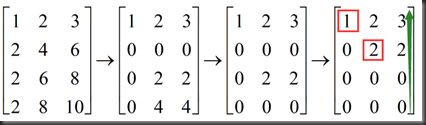
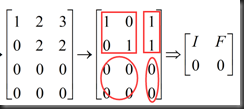
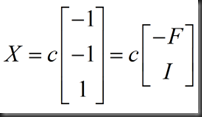
Linear Algebra lecture7 note的更多相关文章
- Linear Algebra lecture1 note
Professor: Gilbert Strang Text: Introduction to Linear Algebra http://web.mit.edu/18.06 Lecture 1 ...
- Linear Algebra lecture9 note
Linear independence Spanning a space Basis and dimension 以上概念都是针对a bunch of vectors, 不是矩阵里的概念 Supp ...
- Linear Algebra lecture10 note
Four fundamental subspaces( for matrix A) if A is m by n matrix: Column space C(A) in Rm (列空间在m维实 ...
- Linear Algebra lecture8 note
Compute solution of AX=b (X=Xp+Xn) rank r r=m solutions exist r=n solutions unique example: 若想方程有解 ...
- Linear Algebra lecture6 note
Vector spaces and subspaces Column space of A solving Ax=b Null space of A Vector space requiremen ...
- Linear Algebra Lecture5 note
Section 2.7 PA=LU and Section 3.1 Vector Spaces and Subspaces Transpose(转置) example: 特殊情况,对称 ...
- Linear Algebra lecture4 note
Inverse of AB,A^(A的转置) Product of elimination matrices A=LU (no row exchanges) Inverse of AB,A^(A ...
- Linear Algebra lecture3 note
Matrix multiplication(4 ways!) Inverse of A Gauss-Jordan / find inverse of A Matrix multiplication ...
- Codeforces Gym101502 B.Linear Algebra Test-STL(map)
B. Linear Algebra Test time limit per test 3.0 s memory limit per test 256 MB input standard input ...
随机推荐
- apache 重定向
<IfModule mod_rewrite.c> RewriteEngine on RewriteCond %{HTTPS} !=on RewriteRule ^(.*) https:// ...
- eclipse 导入工程报错Unable to execute dex: Multiple dex files define Landroid/annotation/SuppressLint
对策: 检查libs 是否有重复加载的.
- js⑧
window对象表示浏览器中打开的窗口, 它是JavaScript浏览器对象模型中的顶层对象.其中还包括了 - Document: 使我们可以从脚本中对 HTML 页面中的所有元素进行访问. - Hi ...
- js操作table
<!DOCTYPE HTML PUBLIC "-//W3C//DTD HTML 4.01 Transitional//EN" "http://www.w3.org/ ...
- x.2
某些原因,和女朋友分手了,难过 订的M18XR3居然提前了半个多月到货,开心 想想一个人的孤单,还是有点难过 转眼间人生已经过去小半,剩下的除去苟延残喘20年,也就不到20年时间蹦跶.都说人生如戏,既 ...
- 19:A*B问题
总时间限制: 1000ms 内存限制: 65536kB 描述 输入两个正整数A和B,求A*B. 输入 一行,包含两个正整数A和B,中间用单个空格隔开.1 <= A,B <= 50000 ...
- DOM扩展之 专有扩展
11.4.3 contains() 方法 用来确定某个节点是不是另一个节点的后代. 注:a.contains(a) 也是返回true.说明contains方法搜索是从自身开始的. DOM Level ...
- vs2013源码编译zlib 1.2.8
1.从 zlib 官网上下载 zlib最新版 1.28 的源码,解压到 zlib-1.2.8 2.使用vs2013打开vc11目录下的sln工程文件(进行单向升级) 3.修改zlibvc工程属性--& ...
- Jenkins - 持续集成环境搭建
1. Jenkins 概述 Jenkins是一个开源的持续集成工具.持续集成主要功能是进行自动化的构建.自动化构建包括自动编译.发布和测试,从而尽快地发现集成错误,让团队能够更快的开发内聚的软件. 2 ...
- The file couldn't be opened because you don't have permission to view it
@import url(http://i.cnblogs.com/Load.ashx?type=style&file=SyntaxHighlighter.css);@import url(/c ...
