1131 Subway Map DFS解法 BFS回溯！

In the big cities, the subway systems always look so complex to the visitors. To give you some sense, the following figure shows the map of Beijing subway. Now you are supposed to help people with your computer skills! Given the starting position of your user, your task is to find the quickest way to his/her destination.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N (≤ 100), the number of subway lines. Then N lines follow, with the i-th (i=1,⋯,N) line describes the i-th subway line in the format:

M S[1] S[2] ... S[M]

where M (≤ 100) is the number of stops, and S[i]'s (i=1,⋯,M) are the indices of the stations (the indices are 4-digit numbers from 0000 to 9999) along the line. It is guaranteed that the stations are given in the correct order -- that is, the train travels between S[i] and S[i+1] (i=1,⋯,M−1) without any stop.

Note: It is possible to have loops, but not self-loop (no train starts from S and stops at S without passing through another station). Each station interval belongs to a unique subway line. Although the lines may cross each other at some stations (so called "transfer stations"), no station can be the conjunction of more than 5 lines.

After the description of the subway, another positive integer K (≤ 10) is given. Then K lines follow, each gives a query from your user: the two indices as the starting station and the destination, respectively.

The following figure shows the sample map.

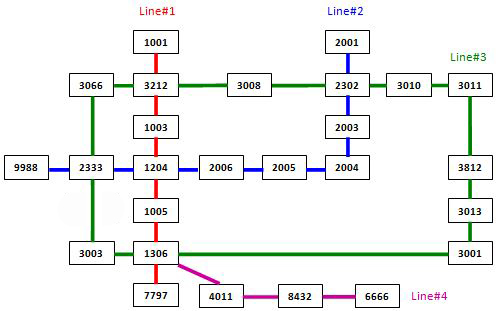
Note: It is guaranteed that all the stations are reachable, and all the queries consist of legal station numbers.

Output Specification:

For each query, first print in a line the minimum number of stops. Then you are supposed to show the optimal path in a friendly format as the following:

where Xi's are the line numbers and Si's are the station indices. Note: Besides the starting and ending stations, only the transfer stations shall be printed.

If the quickest path is not unique, output the one with the minimum number of transfers, which is guaranteed to be unique.

思路：

利用DFS寻找最短路

利用linemap来储存两个站点之间的line

 #include <iostream>
 #include <unordered_map>
 #include <vector>
 using namespace std;
 const int inf = ;
 const int maxn = ;
 vector<int> Graph[maxn];
 unordered_map<int, int> linemap;
 int n,k;
 int mins=inf, mintran=inf;
 vector<int> path,tmppath;
 int vis[maxn];

 int count_trans(vector<int> tmpp){
     int cnt=;
     int idx=linemap[tmpp[]*maxn+tmpp[]];
     for(int i=;i<tmpp.size()-;i++){
         if(linemap[tmpp[i]*maxn+tmpp[i+]]!=idx){
             cnt++;
             idx=linemap[tmpp[i]*maxn+tmpp[i+]];
         }
     }
     return cnt;
 }

 void dfs(int v, int s2){
     tmppath.push_back(v);
     if(v==s2){
         int cnt_trans=count_trans(tmppath);
         if(tmppath.size()<mins||(tmppath.size()==mins&&cnt_trans<mintran)){
             mins=tmppath.size();
             mintran=cnt_trans;
             path=tmppath;
         }
         tmppath.pop_back();
         return;
     }
     for(int i=;i<Graph[v].size();i++){
         if(!vis[Graph[v][i]]){
             vis[Graph[v][i]]=;
             dfs(Graph[v][i], s2);
             vis[Graph[v][i]]=;
         }
     }
     tmppath.pop_back();
 }

 int main(int argc, char *argv[]) {
     fill(vis,vis+maxn,);

     scanf("%d",&n);
     int s1,s2,m;
     for(int i=;i<=n;i++){
         scanf("%d %d",&m,&s1);
         for(int j=;j<m;j++){
             scanf("%d",&s2);
             Graph[s1].push_back(s2);
             Graph[s2].push_back(s1);
             linemap[s1*maxn+s2]=linemap[s2*maxn+s1]=i;
             s1=s2;
         }
     }
     scanf("%d",&k);
     for(int i=;i<k;i++){
         scanf("%d %d",&s1,&s2);
         mins=mintran=inf;
         vis[s1]=;
         dfs(s1,s2);
         vis[s1]=;
         printf("%d\n",mins-);
         int idx=linemap[path[]*maxn+path[]];
         int ls=path[];
         for(int i=;i<path.size()-;i++){
             if(linemap[path[i]*maxn+path[i+]]!=idx){
                 printf("Take Line#%d from %04d to %04d.\n",idx,ls,path[i]);
                 idx=linemap[path[i]*maxn+path[i+]];
                 ls=path[i];
             }
         }
         printf("Take Line#%d from %04d to %04d.\n",idx,ls,s2);
     }
 }

 

不好的BFS

另外还有一种BFS的方法，它的优点是，如果两个站点很近，或者很直接，那么需要遍历的路径就很少，可能就一条：如3011→3001，但像是7797→1001这样的，由于它有很多条相近的路，并且在BFS中是已经出队的点，vis【i】设1，而不是在入队时设1，这样会导致一些节点多次入队

 #include <iostream>
 #include <string>
 #include <algorithm>
 #include <vector>
 #include <queue>
 #include <unordered_map>
 using namespace std;
 const int maxn = ;

 int n;
 vector<int> Graph[maxn];
 unordered_map<int, int> LineMap;
 unordered_map<int, vector<int> > pre;

 vector<int> tmpp,path;
 vector<int> pa;
 int mintrans=;

 void dfs(int v,int s1){
     tmpp.push_back(v);
     if(v==s1){
         int trans=;
         vector<int> tpa;
         for(int i=tmpp.size()-;i>=;i--){
             printf("%d.",tmpp[i]);
         }
         printf("\n");
         /*for(int i=tmpp.size()-1;i>1;i--){
             if(LineMap[tmpp[i]*maxn+tmpp[i-1]]!=LineMap[tmpp[i-1]*maxn+tmpp[i-2]]){
                 trans++;
                 tpa.push_back(tmpp[i-1]);
                 //printf("*\n");
             }
         }
         if(trans<mintrans){
             mintrans=trans;
             pa=tpa;
             path=tmpp;
         }*/
         tmpp.pop_back();
         return;
     }
     for(int i=;i<pre[v].size();i++){
         dfs(pre[v][i],s1);
     }
     tmpp.pop_back();
     return;
 }

 void BFS(int s1,int s2){
     for(unordered_map<int, vector<int> >::iterator it=pre.begin();it!=pre.end();it++){
         it->second.clear();
     }
     int vis[maxn];    fill(vis,vis+maxn,);
     queue<int> q;
     int lv=;
     int last=s1 ,llast=s1;
     q.push(s1);
     vis[s1]=;
     while (q.size()) {
         int top=q.front(); q.pop();
         vis[top]=;
         printf("top=%d\n",top);
         if(top==s2) break;
         for(int i=;i<Graph[top].size();i++){
             if(!vis[Graph[top][i]]){
                 q.push(Graph[top][i]);
                 pre[Graph[top][i]].push_back(top);
                 llast=Graph[top][i];
                 printf("%d,",Graph[top][i]);
             }
         }
         printf("\n");
     }
     printf("\n");
     for(int i=;i<pre[].size();i++){
         printf("%d ;",pre[][i]);
     }printf("\n");
     dfs(s2,s1);

 }

 int main(){
     scanf("%d",&n);
     int m;
     for(int i=;i<=n;i++){
         scanf("%d",&m);
         int s1,s2;
         scanf("%d",&s1);
         for(int j=;j<m;j++){
             scanf("%d",&s2);
             Graph[s1].push_back(s2);
             Graph[s2].push_back(s1);
             LineMap[s1*maxn+s2]=i;
             LineMap[s2*maxn+s1]=i;
             s1=s2;
         }
     }
     int k;
     scanf("%d",&k);
     int s1,s2;
     for(int i=;i<k;i++){
         scanf("%d %d",&s1,&s2);
         BFS(s1,s2);
     }
 }

top=7797
1306,
top=1306
1005,3001,3003,4011,
top=1005
1204,
top=3001
3013,
top=3003
2333,
top=4011
8432,
top=1204
1003,2333,2006,
top=3013
3812,
top=2333
9988,3066,
top=8432
6666,
top=1003
3212,
top=2333
9988,3066,
top=2006
2005,
top=3812
3011,
top=9988

top=3066
3212,
top=6666

top=3212
1001,3008,
top=9988

top=3066

top=2005
2004,
top=3011
3010,
top=3212
1001,3008,
top=1001

3212 ;3212 ;
2333 ;2333 ;
7797.1306.1005.1204.1003.3212.1001.
7797.1306.3003.2333.3066.3212.1001.
7797.1306.1005.1204.2333.3066.3212.1001.
7797.1306.3003.2333.3066.3212.1001.
7797.1306.1005.1204.2333.3066.3212.1001.
7797.1306.1005.1204.1003.3212.1001.
7797.1306.3003.2333.3066.3212.1001.
7797.1306.1005.1204.2333.3066.3212.1001.
7797.1306.3003.2333.3066.3212.1001.
7797.1306.1005.1204.2333.3066.3212.1001.

这些重复都是多次入队的结果，可以看出，太远的路就不会被遍历了，但是会有重复遍历的情况

 好的BFS

参考 https://blog.csdn.net/a799581229/article/details/79176455

 /*************************
 题意:
 一个特殊的地铁图
 求s到e的最短距离路线
 如果距离相同，求换乘次数最少的路线
 ************************/
 /***********************
 解题思路：
 由于点可能有10000个，用dijkstr容易超时
 而这里的特点是只有100条地铁站，每个点最多5个度
 即有很多情况是只有1个选择的情况（笔直向下走）
 因此，我们选择使用BFS，能充分利用这个特性。
 储存图是要把边也存进去，为了判断是否换乘，我们是利用边的组id去判断的。
 入队的是行进状态State
     该状态包括当前站，当前线路组id，当前行进距离，和当前换乘距离
 然后利用优先队列去做队列
 因为结果不唯一，所以我们可以设置一个vis[]，已经出队的点，就设置vis=1
 接下来这个点不需要再入队。
 处理要怎么计算换乘和储存换乘节点即可。
 *************************/
 /***********************
 注意：
     优先bfs时，注意vis只在入队时判断，只在出队时去设1
 *********************/
 #include<iostream>
 #include<stdio.h>
 #include<string>
 #include<vector>
 #include<queue>
 #include<stdlib.h>
 #include<algorithm>
 #include<string.h>
 #include<stack>
 #include<map>
 #include<set>
 #include<unordered_map>
 using namespace std;
 #define M 10005
 #define INF 0x7ffffff

 vector<int> edg[M];
 struct Road{
     int s;
     int e;
     int id;
 };
 Road road[M];

 struct State{
     int dis;
     int cnum; //change num
     int nowcity;
     int nowroad;
     vector<int> cv;
     vector<int> rv;
     bool operator < (const State & a) const{
         if(dis > a.dis)
             return true;
         else if(dis == a.dis)
             return cnum > a.cnum;
         else return false;
     }
 };
 int vis[M];
 void dijk(int start,int end){
     int i;
     priority_queue<State> q;
     memset(vis,,sizeof(vis));
     State sta;
     sta.cnum = ;
     sta.nowcity = start;
     sta.dis = ;
     sta.nowroad = -;
     q.push(sta);
     int city;
     Road r;
     int e;
     State pushs;
     while(!q.empty()){
         sta = q.top();
         q.pop();
         city = sta.nowcity;
         vis[city] = ;
         if(city == end){
             int lastc;
             sta.cv.push_back(end);
             cout<<sta.dis<<endl;
             for(i = ;i < sta.rv.size();i++){
                 printf("Take Line#%d from %04d to %04d.\n",sta.rv[i],sta.cv[i],sta.cv[i+]);
             }
             break;
         }
         for(i = ;i < edg[city].size();i++){
             pushs = sta;
             r = road[edg[city][i]];
             if(r.s == city)
                 e = r.e;
             else e = r.s;

             if(vis[e])
                 continue;
             if(r.id != sta.nowroad){
                 pushs.cnum++;
                 pushs.cv.push_back(sta.nowcity); //将变换处的起点放入
                 pushs.rv.push_back(r.id);
                 pushs.nowroad = r.id;
             }
             pushs.dis++;
             pushs.nowcity = e;
             q.push(pushs);
         }
     }
 }

 int main(){
     int n, i, m, k;
     int j,node,lastnode;
     scanf("%d",&n);

     j=;
     for(i = ;i <= n;i++){
         scanf("%d",&k);
         lastnode = -;
         while(k--){
             scanf("%d",&node);
             if(lastnode != -){
                 edg[lastnode].push_back(j);
                 edg[node].push_back(j);
                 road[j].s = lastnode;
                 road[j].e = node;
                 road[j].id = i;
                 j++;
             }
             lastnode = node;
         }
     }
     cin>>k;
     int s, e;
     while(k--){
         cin>>s>>e;
         dijk(s,e);
     }

     return ;
 }