BZOJ1005--[HNOI2008]明明的烦恼(树的prufer编码)
1005: [HNOI2008]明明的烦恼
Time Limit: 1 Sec Memory Limit: 162 MB
Submit: 5768 Solved: 2253
[Submit][Status][Discuss]
Description
自从明明学了树的结构,就对奇怪的树产生了兴趣......给出标号为1到N的点,以及某些点最终的度数,允许在
任意两点间连线,可产生多少棵度数满足要求的树?
Input
第一行为N(0 < N < = 1000),
接下来N行,第i+1行给出第i个节点的度数Di,如果对度数不要求,则输入-1
Output
一个整数,表示不同的满足要求的树的个数,无解输出0
Sample Input
1
-1
-1
Sample Output
HINT
两棵树分别为1-2-3;1-3-2
转自怡红公子(http://www.cnblogs.com/noip/archive/2013/03/10/2952520.html)----
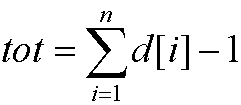
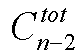 种插法;
种插法;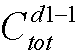 种插法;
种插法;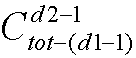 种插法;
种插法;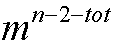 ;
;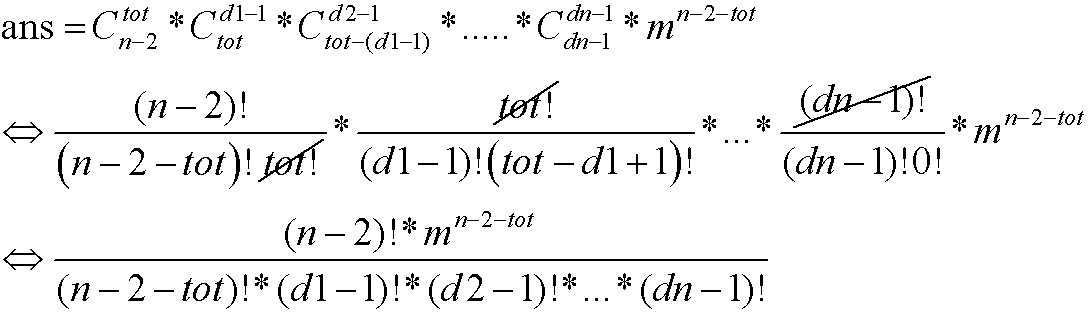
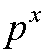 ,其中
,其中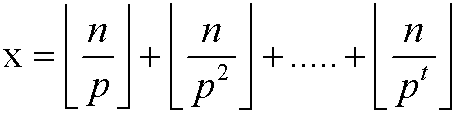 且
且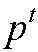 <n
<n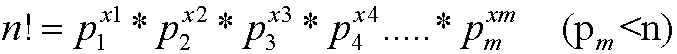
BZOJ1005--[HNOI2008]明明的烦恼(树的prufer编码)的更多相关文章
- bzoj 1005: [HNOI2008]明明的烦恼 树的prufer序列+万进制
题目传送门 思路: 这道题需要前置知识prufer编码,这篇博客对prufer编码和这道题的分析写的很好. 这里主要讲一些对大数阶乘的分解,一个办法当然是用高精度,上面这篇博客用的是java,还有一个 ...
- bzoj1005: [HNOI2008]明明的烦恼(prufer+高精度)
1005: [HNOI2008]明明的烦恼 题目:传送门 题解: 毒瘤题啊天~ 其实思考的过程还是比较简单的... 首先当然还是要了解好prufer序列的基本性质啦 那么和1211大体一致,主要还是利 ...
- bzoj1005 [HNOI2008]明明的烦恼
1005: [HNOI2008]明明的烦恼 Time Limit: 1 Sec Memory Limit: 162 MBSubmit: 3032 Solved: 1209 Description ...
- [BZOJ1005] [HNOI2008] 明明的烦恼 (prufer编码)
Description 自从明明学了树的结构,就对奇怪的树产生了兴趣......给出标号为1到N的点,以及某些点最终的度数,允许在任意两点间连线,可产生多少棵度数满足要求的树? Input 第一行为N ...
- [bzoj1005][HNOI2008][明明的烦恼] (高精度+prufer定理)
Description 自从明明学了树的结构,就对奇怪的树产生了兴趣......给出标号为1到N的点,以及某些点最终的度数,允许在任意两点间连线,可产生多少棵度数满足要求的树? Input 第一行为N ...
- 【prufer编码+组合数学】BZOJ1005 [HNOI2008]明明的烦恼
Description 自从明明学了树的结构,就对奇怪的树产生了兴趣...... 给出标号为1到N的点,以及某些点最终的度数,允许在任意两点间连线,可产生多少棵度数满足要求的树? Solution 这 ...
- BZOJ1005:[HNOI2008]明明的烦恼(组合数学,Prufer)
Description 自从明明学了树的结构,就对奇怪的树产生了兴趣......给出标号为1到N的点,以及某些点最终的度数,允许在任意两点间连线,可产生多少棵度数满足要求的树? Input 第一行为N ...
- bzoj1005: [HNOI2008]明明的烦恼 prufer序列
https://www.lydsy.com/JudgeOnline/problem.php?id=1005 给出标号为1到N的点,以及某些点最终的度数,允许在任意两点间连线,可产生多少棵度数满足要求的 ...
- [bzoj1005][HNOI2008]明明的烦恼-Prufer编码+高精度
Brief Description 给出标号为1到N的点,以及某些点最终的度数,允许在 任意两点间连线,可产生多少棵度数满足要求的树? Algorithm Design 结论题. 首先可以参考这篇文章 ...
- BZOJ1005 HNOI2008明明的烦恼(prufer+高精度)
每个点的度数=prufer序列中的出现次数+1,所以即每次选一些位置放上某个点,答案即一堆组合数相乘.记一下每个因子的贡献分解一下质因数高精度乘起来即可. #include<iostream&g ...
随机推荐
- WMIC命令的利用技巧
WMIC扩展WMI(Windows Management Instrumentation,Windows管理工具),提供了从命令行接口和批命令脚本执行系统管理的支持.在WMIC出现之前,如果要管理WM ...
- eclipse导入maven空项目,eclipse导入时不识别maven项目
经常我们在网上下载的一些开源项目中,想要导入eclipse中,却发现eclipse不识别这个项目,这时候怎么办呢? 解决办法多种多样,我这里举例出最实用的2种: 1.在项目的根目录中加入.classp ...
- 在开源UOJ的导航栏中添加新页面链接
前言 刚用开源UOJ搭建OJ成功时就想在导航栏那里添加一个站内页面链接,无奈当时乱搞水平低,网上也没有教程,不晓得怎么弄 今天突然来了闲情乱搞一通,结果还真乱搞成了...特意写下为后来人少走点弯路 前 ...
- PM2 部署 nodejs API项目
PM2的主要特性: 内建负载均衡(使用Node cluster 集群模块) 后台运行 0秒停机重载,我理解大概意思是维护升级的时候不需要停机. 具有Ubuntu和CentOS 的启动脚本 停止不稳定的 ...
- c#调用存储过程实现批量增加和修改数据
1 例如当我在编辑表格数据,一次编辑了多行需要保存到数据库时,就需要判断数据库中是否已经存在,存在则修改,不存在则新增一条或多条数据,即所谓批量增加或者跟新数据. 首先需要构建数据包,把要添加或者跟新 ...
- 客户想要的 vs 客户实际预算:漫画解读软件开发模式
转自:http://blog.jobbole.com/113230/ 1913 年,美利坚工业之神——亨利福特,发明了世界上第一条流水线,汽车工业从此进入了大规模生产的时代.丰田公司提出的丰田生产系统 ...
- Django的ORM获取单表数据的三种方法
前言主题是从数据库取数据,把数据展现到前端客户端 一共有三种方法如下: 1,以对象的方法: 2,以字典的方法: 3,以元组的方法: 以对象的方法 说明:获取的是QuerySet类型,输出的是每个元素都 ...
- 《浏览器工作原理与实践》<05>渲染流程(上):HTML、CSS和JavaScript,是如何变成页面的?
在上一篇文章中我们介绍了导航相关的流程,那导航被提交后又会怎么样呢?就进入了渲染阶段.这个阶段很重要,了解其相关流程能让你“看透”页面是如何工作的,有了这些知识,你可以解决一系列相关的问题,比如能熟练 ...
- linux基础4-压缩及其相关的命令
一 压缩的原理以及gzip.bzip2.tar三个命令的: Linux下文件的压缩与打包 二 zip.zipinfo.unzip: zip:压缩成.zip文件 zipinfo:列出压缩文件信息
- 2.01_Python网络爬虫概述
一:什么是网络爬虫 网络爬虫(又被称为网页蜘蛛,网络机器人,在FOAF社区中间,更经常的称为网页追逐者),是一种按照一定的规则,自动地抓取网络信息的程序或者脚本: 二:为什么要做网络爬虫? 大数据时代 ...
