Interviewe(hdu3486)

Interviewe

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 6689    Accepted Submission(s): 1582

Problem Description

YaoYao has a company and he wants to employ m people recently. Since his company is so famous, there are n people coming for the interview. However, YaoYao is so busy that he has no time to interview them by himself. So he decides to select exact m interviewers for this task.
YaoYao decides to make the interview as follows. First he queues the interviewees according to their coming order. Then he cuts the queue into m segments. The length of each segment is 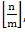, which means he ignores the rest interviewees (poor guys because they comes late). Then, each segment is assigned to an interviewer and the interviewer chooses the best one from them as the employee.
YaoYao’s idea seems to be wonderful, but he meets another problem. He values the ability of the ith arrived interviewee as a number from 0 to 1000. Of course, the better one is, the higher ability value one has. He wants his employees good enough, so the sum of the ability values of his employees must exceed his target k (exceed means strictly large than). On the other hand, he wants to employ as less people as possible because of the high salary nowadays. Could you help him to find the smallest m?

 

Input

The input consists of multiple cases.
In the first line of each case, there are two numbers n and k, indicating the number of the original people and the sum of the ability values of employees YaoYao wants to hire (n≤200000, k≤1000000000). In the second line, there are n numbers v1, v2, …, vn (each number is between 0 and 1000), indicating the ability value of each arrived interviewee respectively.
The input ends up with two negative numbers, which should not be processed as a case.

 

Output

For each test case, print only one number indicating the smallest m you can find. If you can’t find any, output -1 instead.

 

Sample Input

11 300
7 100 7 101 100 100 9 100 100 110 110
-1 -1

 

Sample Output

3

Hint

We need 3 interviewers to help YaoYao. The first one interviews people from 1 to 3, the second interviews people from 4 to 6,
and the third interviews people from 7 to 9. And the people left will be ignored. And the total value you can get is 100+101+100=301>300.

思路：RMQ;

先RMQ处理好区间最大值，首先（sqrt（n））枚举分成多少组，然后O(n)检测，这个时候再考虑每组多少人，我们可以知道枚举多少组的时候，我们把每组（sqrt(n),n）都能包括进去，那后就剩每组[1,sqrt(n)-1]的人这种没处理，然后再[1,sqrt(n)]枚举每组的多少人，然后检验，但这个检验的时候要遵循，最小的原则；比如 12 6

111111111111，是5，然么当每组取两个的时候，只要到第5组就可以了，因为12/5=2,12/6=2;复杂度（n×sqrt（n））；

 1 #include<stdio.h>
 2 #include<algorithm>
 3 #include<iostream>
 4 #include<string.h>
 5 #include<queue>
 6 #include<deque>
 7 #include<stack>
 8 #include<math.h>
 9 using namespace std;
10 typedef long long LL;
11 int ans[200005];
12 void RMQ(int n);
13 int mnsum[200005][22];
14 int mm[200005];
15 int rmq(int x, int y);
16 int  check(int n,int k,int s);
17 int main(void)
18 {
19     int n;
20     int  k;
21     while(scanf("%d %d",&n,&k),n>0&&k>0)
22     {
23         int i;
24         int sum = 0;
25         int minn = -1;
26         for(i = 1; i <= n; i++)
27         {
28             scanf("%d",&ans[i]);
29             sum += ans[i];
30         }
31         if(sum <= k)printf("-1\n");
32         else
33         {
34             RMQ(n);
35             for(i = 1; i <= sqrt(1.0*n); i++)
36             {
37                 int x = n/i;
38                 int xx = check(n,x,k);
39                 if(xx!=-1)
40                 {
41                     minn = xx;
42                     break;
43                 }
44             }
45             if(minn == -1)
46             {
47                 int y = n/(sqrt(1.0*n))-1;
48                 for(i = y; i >= 1; i--)
49                 {
50                     int xx = check(n,i,k);
51                     if(xx!=-1)
52                     {
53                         minn = xx;
54                         break;
55                     }
56                 }
57             }
58             printf("%d\n",minn);
59         }
60     }
61     return 0;
62 }
63 void RMQ(int n)
64 {
65     mm[0] = -1;
66     for(int i = 1; i<=n; i++)
67     {
68         mm[i] = ((i&(i-1)) == 0) ? mm[i-1]+1:mm[i-1];
69         mnsum[i][0] = ans[i];
70     }
71     for(int j = 1; j<=mm[n]; j++)
72         for(int i = 1; i+(1<<j)-1<=n; i++)
73             mnsum[i][j] = max(mnsum[i][j-1], mnsum[i+(1<<(j-1))][j-1]);
74 }
75 int rmq(int x, int y)
76 {
77     int k = mm[y-x+1];
78     return max(mnsum[x][k], mnsum[y-(1<<k)+1][k]);
79 }
80 int  check(int n,int k,int s)
81     {   //if(k==1)printf("1\n");
82         int sum = 0;
83         int i;
84         int cnt = 0;
85         for(i = 1; i+k-1<= n; i+=k)
86         {
87             cnt++;
88             sum += rmq(i,i+k-1);
89             if(sum > s)return cnt;//最小原则；
90         }
91         return -1;
92     }