【HDU6662】Acesrc and Travel(树型Dp)

题目链接

大意

给出一颗树，每个点上有一个权值\(A[i]\)，有两个绝顶聪明的人甲和乙。

甲乙两人一起在树上轮流走，不能走之前经过的点。（甲乙时刻在一起）

甲先手，并可以确定起点。甲想要走过的点权之和最大，乙想要权值和最小。

求最终权值和。

思路

首先有个很明显的想法就是树形Dp：

设\(F0[u]\)表示以\(u\)为根的子树内，甲先手，以\(u\)为起点的权值和。

设\(F1[u]\)表示以\(u\)为根的子树内，乙先手，以\(u\)为起点的权值和。

那么转移式就为：

\(F0[u]=Min(F1[v])+A[u]\)

\(F1[u]=Max(F0[v])+A[u]\)

其中\(v\)为\(u\)的一个儿子。

这样我们可以处理出每个点只在其子树范围走内的答案。

---

考虑从某个点出发，向上走形成的答案。



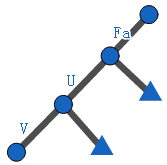
我们设\(TP[V]\)表示不走\(V\)的子树，甲先手，以\(V\)为起点的权值和。

那么\(TP[V]\)的更新就会有两种情况，一种是先走\(U\)，然后再走\(U\)的某个儿子。



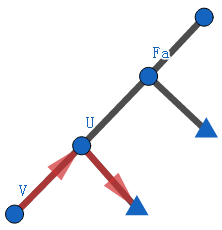
对于这种情况，甲肯定会选\(U\)的儿子中\(F0\)最大的值，即\(F1[U]\)。

但又由于\(V\)可能本身就是最大的，所以应该记录下\(F1\)的最大值与次大值进行转移。

对于另一种，就是先走\(U\)，再走\(Fa\)的情况。



对于这种情况，在走到\(Fa\)时，\(B\)肯定会选择较小的那一边走。

所以就是\(Fa\)所有儿子中最小的\(F1\)，即\(F0[Fa]\)与\(Fa\)向上走的情况\(TP[Fa]\)取较小值就行了。

但同理，\(U\)可能是最小的，所以记录下\(F0\)的最小值与次小值进行转移。

对于以上两种\(TP\)情况的选择由于是\(A\)选，所以取较大值。

注：在转移\(TP\)时，时刻注意为一条链的情况。

最后枚举以哪一个点为起点，取\(F0[U][0]\)与\(TP[U]\)的较小值就行了。

注意叶子节点与根的取值。

代码

细节超多，易错点主要集中在初值的赋值以及根上。

#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;
const int MAXN=600005;
const long long INF=1e17;
int K,N,A[MAXN];
int son0[MAXN],son1[MAXN];
long long Ans;
long long F0[MAXN][2],F1[MAXN][2];//0:A|||||||1:B
long long TP[MAXN];
vector<int>P[MAXN];
void DFS(int u,int fa){
	int Ok=0;
	int size=P[u].size();
	for(int i=0;i<size;i++){
		int v=P[u][i];
		if(v==fa)continue;
		DFS(v,u);Ok=1;
		if(F1[v][0]+A[u]<F0[u][0])F0[u][1]=F0[u][0],F0[u][0]=min(F0[u][0],F1[v][0]+A[u]),son0[u]=v;
		else F0[u][1]=min(F0[u][1],F1[v][0]+A[u]);
		if(F0[v][0]+A[u]>F1[u][0])F1[u][1]=F1[u][0],F1[u][0]=max(F1[u][0],F0[v][0]+A[u]),son1[u]=v;
		else F1[u][1]=max(F1[u][1],F0[v][0]+A[u]);
	}
	if(!Ok)F0[u][0]=F0[u][1]=F1[u][0]=F1[u][1]=A[u];
}
void DFS2(int u,int fa){
	int size=P[u].size();
	for(int i=0;i<size;i++){
		int v=P[u][i];
		if(v==fa)continue;
		long long val1=INF,val2=INF;
		if(P[u].size()!=2){
			if(son1[u]==v)val1=F1[u][1];
			else val1=F1[u][0];
		}else val1=u==1?A[u]:-INF;
		if(P[fa].size()!=2){
			if(son0[fa]==u)val2=F0[fa][1];
			else val2=F0[fa][0];
		}val2=min(val2,TP[fa]);
		TP[v]=A[v]+max(val1,val2+A[u]);
		DFS2(v,u);
	}
}
int main(){
	//freopen("data.txt","r",stdin);
	//freopen("mine.txt","w",stdout);
	scanf("%d",&K);
	while(K--){
		scanf("%d",&N);
		for(int i=0;i<=N;i++){
			F0[i][0]=F0[i][1]=INF;
			F1[i][0]=F1[i][1]=-INF;
			son0[i]=son1[i]=0;TP[i]=-INF;
			P[i].clear();
		}
		for(int i=1;i<=N;i++)scanf("%d",&A[i]);
		for(int i=1,x;i<=N;i++)scanf("%d",&x),A[i]-=x;
		if(N==1){
			printf("%d\n",A[1]);
			continue;
		}
		for(int i=1,x,y;i<N;i++){
			scanf("%d%d",&x,&y);
			P[x].push_back(y);
			P[y].push_back(x);
		}Ans=-INF;P[1].push_back(0);
		DFS(1,0);
		if(P[1].size()!=2)TP[1]=INF;
		else TP[1]=A[1];
		DFS2(1,0);
		Ans=F0[1][0];
		for(int i=2;i<=N;i++){
			if(P[i].size()==1)Ans=max(Ans,TP[i]);
			else Ans=max(Ans,min(F0[i][0],TP[i]));
		}
		printf("%lld\n",Ans);
	}
}