BUAA软件工程个人项目作业

BUAA软件工程个人项目作业

项目	内容
这个作业属于哪个课程	2020春季计算机学院软件工程(罗杰 任健)
这个作业的要求在哪里	个人项目作业
我在这个课程的目标是	学习软件开发的流程
这个作业在哪个具体方面帮助我实现目标	体会个人写项目的流程
教学班级	006
项目地址	https://github.com/monokuma-zhuo/Intersect

PSP项目表格

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划
· Estimate	· 估计这个任务需要多少时间	10	10
Development	开发
· Analysis	· 需求分析 (包括学习新技术)	30	60
· Design Spec	· 生成设计文档	20	30
· Design Review	· 设计复审 (和同事审核设计文档)	20	20
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	5	5
· Design	· 具体设计	30	15
· Coding	· 具体编码	120	100
· Code Review	· 代码复审	15	30
· Test	· 测试（自我测试，修改代码，提交修改）	60	120
Reporting	报告
· Test Report	· 测试报告	10	30
· Size Measurement	· 计算工作量	5	10
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	10	15
	合计	335	445

解题思路描述

读懂题目后，明白题目要求是平面内求直线和圆的交点总数。思路大概分为如何求解该问题和用代码如何实现

如何求解

很显然用解析几何知识，对于所有曲线两两求交点。因此我查找并复习了一些解析几何知识，并确定解题方法。

直线方程最常用的形式有点斜式y=kx+b和标准式Ax+By+C=0。点斜式虽然在运算时方便，但由于要考虑斜率等于0和斜率不存在的情况比较麻烦，故直线方程选择了标准式。

圆方程有标准式(x-a)²+(y-b)²=r²和一般式x²+y²+Dx+Ey+F=0两种形式，由于输入数据直接给出了圆心坐标和半径，我也没有多考虑直接选择了第一种形式。

直线与直线有平行和相交两种情况(重合不考虑)，平行则A1*B2=A2*B1，否则直接联立求解即可。

直线与圆有相交相切相离三种情况，可以利用圆心到直线的距离是否大于半径来判断位置关系，也可以直接联立方程组根据解的个数判断，并得到交点坐标。

圆与圆有内含、内切、相交、外切、相离5种情况，可以利用两个圆心之间的距离判断位置关系，在求解时需要用到圆的一般式，相减去掉平方项后得到一个直线方程，之后用该直线方程和任意一个圆联立即可得到交点坐标。

代码实现

首先考虑到如何存储直线、圆、点，查找并学习了许多c++的容器，比如这次用到的vector，set，pair。

最初是想把点封装为一个类，但由于本题目只需要点的数量，放弃了封装类，仅存在了vector容器中。每个点由横坐标和纵坐标组成，故想到利用pair将x和y组合在一起，所以需要vector<pair>这样的容器。由于可能会有交点重复的情况，所以还需要对vector中的元素去重，将vector排序后用unique和erase进行去重。此外了解到set容器使用红黑树的结构并且不支持重复元素，故也可以直接用set进行存储。

线需要创建一个类，其中包含A,B,C三个参数的值，以及一个求交点坐标的intersect方法，返回值是pair类型。由于该方法我希望直接返回交点的坐标，所以我又写了一个方法判断两直线是否相交，如果相交则再调用intersect方法求坐标，这样也省去了一些不必要的计算。

同理圆也创建一个类，其中包含圆心坐标(a,b)和半径r三个参数。方法借鉴了线类的思想，先判断圆和直线是否有交点，如果有则调用line_cycle_instere方法求得交点坐标。返回值是一个pair<pair,pair>的形式，返回两个交点(如果相切，则相当于两个交点是同一点)。同理，判断两圆是否有交点，如果有则调用cycle_cycle_instere方法求得交点坐标。

设计与测试

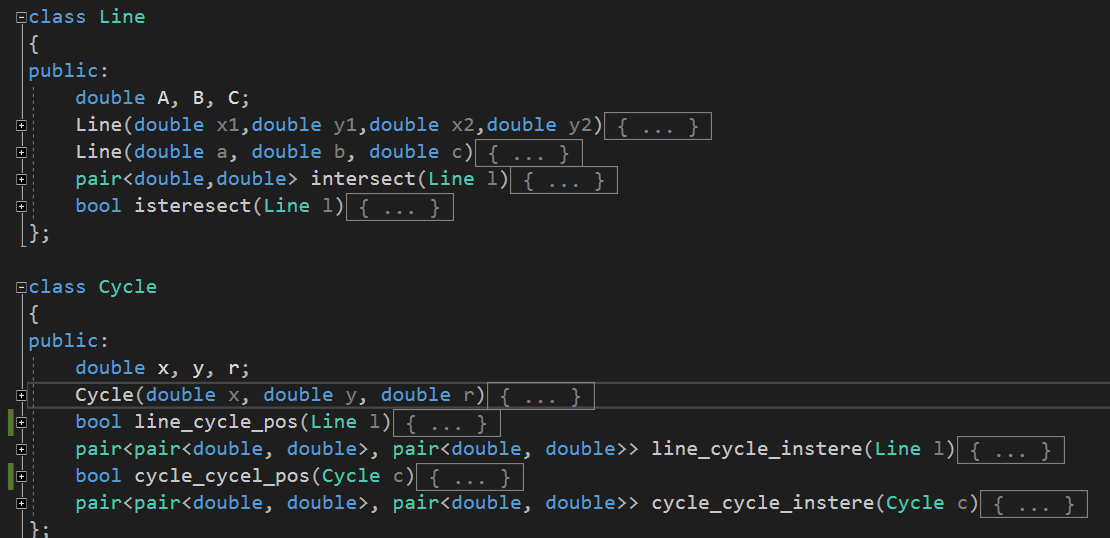
如图共有两个类，Line类有2个构造函数和2个方法，Cycle类有1个构造函数和4个方法。这里我说一下为什么Line类为什么会多一个构造函数，因为根据两圆相交求交点的方法，是会直接得到Ax+By+C=0形式的直线方程。而输入的直线方程是两个点的坐标，二者不同，所以我重载了构造函数，得到直线后再调用line_cycle_instere方法即可。二者之间仅在圆和直线有交点时，Cycle对象会传入一个Line对象并进行求交点的运算。

这次题目比较简单，所以没有画流程图。大致说一下main函数的流程，读入数据后判断是直线还是圆并建立相应的对象存到vector容器中，之后判断该直线或圆有没有和已有的直线和圆相交，如果有则计算交点坐标并存入set容器。最后输出set容器的size即可。

单元测试根据之前分析的情况，针对直线和圆的不同位置关系构造不同的数据。包括：直线与直线相交、平行；直线与圆相交、相切、相离；圆与圆内含、内切、相交、外切、相离。其中还夹杂着直线斜率为0，直线斜率不存在以及重复点的情况。

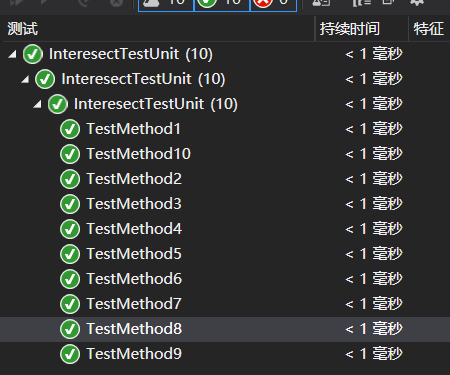
性能分析与改进

在进行性能分析时发现消耗最大的是set容器的insert方法。随着交点增多，树的深度也逐渐加深，这样每进行一次insert就要消耗log数深的复杂度。所以我想到改用vector，毕竟vector的push_back方法是O(1)的复杂度。但经实际测试发现效果并不好，原因是vector在空间不够时，会讲整个数组拷贝到另一份新空间中。这样在数据量大的情况下会经常出现空间不够的情况，就需要反复进行O(n)的操作，代价也非常大，所以权衡之下还是选择了set容器。

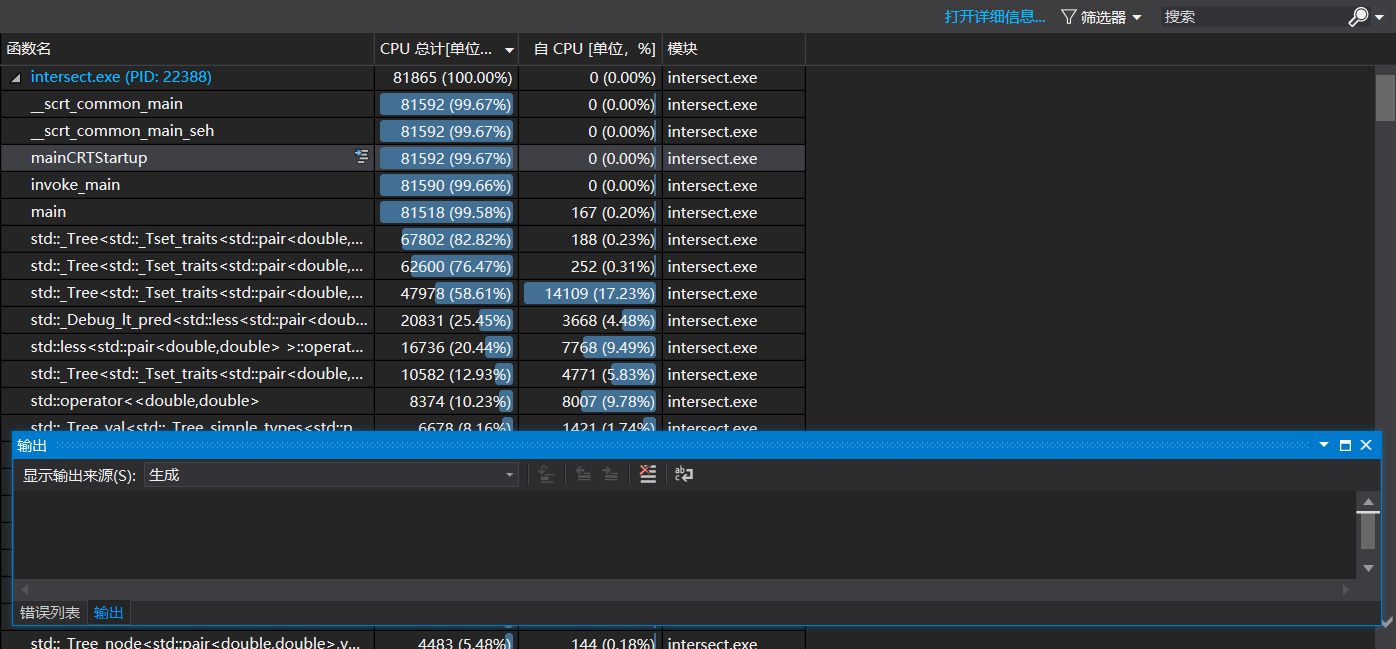
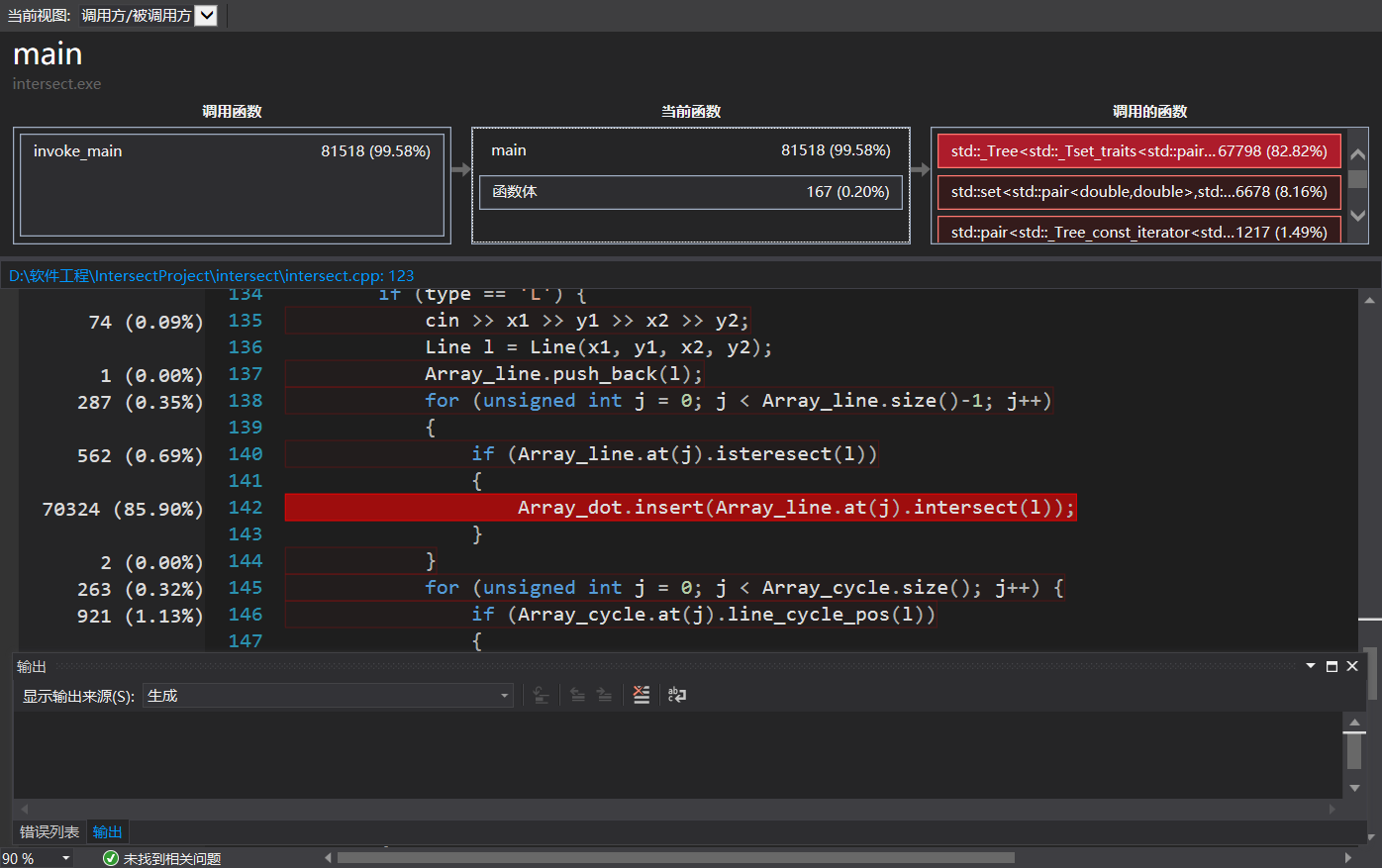
如图这是我随机生成的10000条直线和圆的结果，消耗最大的地方为set容器的insert方法（上图数据仅供参考，实际的交点数已远大于题目要求）

代码说明

pair<double,double> intersect(Line l)
{
	double x = (l.C * B - C * l.B) / (A * l.B - B * l.A);
	double y = (C * l.A - l.C * A) / (A * l.B - B * l.A);
	pair<double, double> dot(x, y);
	return dot;
}

求两直线交点坐标，联立解方程组即可。

bool isteresect(Line l)
{
	if (A * l.B - B * l.A == 0)
	{
		return false;
	}
	else
	{
		return true;
	}
}

判断两直线是否平行。

bool line_cycle_pos(Line l)
{
	double length = abs((l.A * x + l.B * y + l.C)) / (sqrt(l.A * l.A + l.B * l.B));
	if (length > r)
	{
		return false;
	}
	else
	{
		return true;
	}
}

判断圆和直线的位置关系，利用点到直线距离公式求圆心到直线的距离。

    pair<pair<double, double>, pair<double, double>> line_cycle_instere(Line l)
	{
		if (l.A == 0)
		{
			double y_point = -1.0 * l.C / l.B;
			double temp = sqrt((r * r - (y - y_point) * (y - y_point)));
			pair<double, double> dot1(x + temp, y_point);
			pair<double, double> dot2(x - temp, y_point);
			return make_pair(dot1, dot2);
		}
		else if (l.B == 0)
		{
			double x_point = -1.0 * l.C / l.A;
			double temp = sqrt((r * r - (x - x_point) * (x - x_point)));
			pair<double, double> dot1(x_point, y + temp);
			pair<double, double> dot2(x_point, y - temp);
			return make_pair(dot1, dot2);
		}
		else
		{
			double k = -1.0 * l.A / l.B;
			double b = -1.0 * l.C / l.B;
			double a1 = 1.0 + k * k;
			double b1 = 2.0 * (k * b - k * y - x);
			double c1 = (b - y) * (b - y) -(r * r)+(x*x);
			double x1 = (-1.0 * b1 + sqrt(b1 * b1 - 4 * a1 * c1)) / (2.0 * a1);
			double y1 = k * x1 + b;
			double x2 = (-1.0 * b1 - sqrt(b1 * b1 - 4 * a1 * c1)) / (2.0 * a1);
			double y2 = k * x2 + b;
			pair<double, double> dot1(x1, y1);
			pair<double, double> dot2(x2, y2);
			return make_pair(dot1, dot2);
		}
	}

求直线和圆交点坐标。分别判断了斜率等于0，斜率不存在的情况。然后将直线方程转化为y=kx+b的形式与圆方程进行联立求解。最后利用一元二次方程的求根公式得到x1和x2，带回到直线方程中即可求得y1和y2

bool cycle_cycel_pos(Cycle c)
{
	double length = sqrt((c.x - x) * (c.x - x) + (c.y - y) * (c.y - y));
	if (length > r + c.r||length<abs(r-c.r))
	{
		return false;
	}
	else
	{
		return true;
	}
}

判断两圆的位置关系，求得圆心之间的距离，如果距离大于半径加和则外离；小于半径差则内含，都没有交点，其他情况均有交点。

pair<pair<double, double>, pair<double, double>> cycle_cycle_instere(Cycle c)
{
	double D = -2.0 * x;
	double E = -2.0 * y;
	double F = (x * x) + (y * y) - (r * r);
	double D1 = -2.0 * c.x;
	double E1 = -2.0 * c.y;
	double F1 = (c.x * c.x) + (c.y * c.y) - (c.r * c.r);
	Line temp_l(D - D1, E - E1, F - F1);
	return line_cycle_instere(temp_l);
}

求两圆的交点坐标，将圆转化为一般式后相减即得到一个直线方程，然后调用直线与圆求交点的方法即可。

最后附上代码已无任何警告的截图。