SLAM的数学基础（4）：先验概率、后验概率、贝叶斯准则

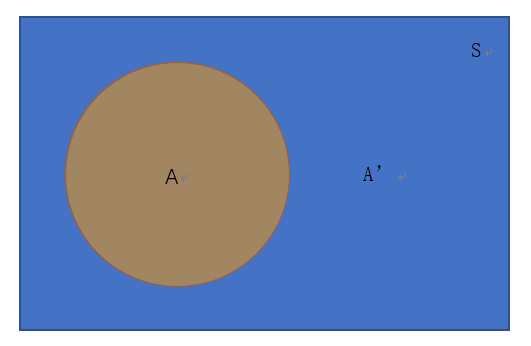
假设有事件A和事件B，可以同时发生但不是完全同时发生，如以下韦恩图所示：

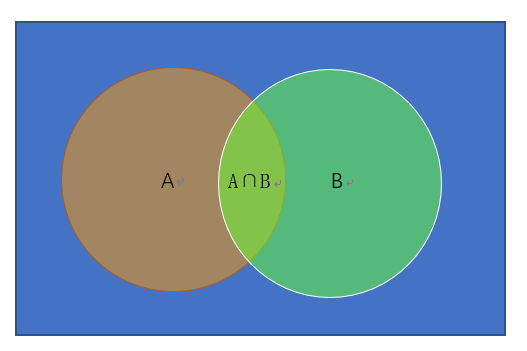
其中，A∩B表示A和B的并集，即A和B同时发生的概率。

如此，我们很容易得出，在事件B发生的情况下，事件A发生的概率为：

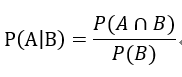
这个P(A|B)就是条件概率(Conditional Probability)。

同理，在事件A发生的情况下，事件B发生的概率为：

由以上式子可得：

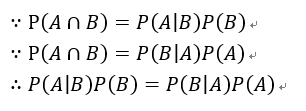
再调整一下，变成：

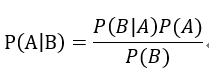
这个就是著名的贝叶斯公式的基本形态了，其中：

P(A|B)叫做后验概率(Posterior Probability)

P(A)叫做先验概率(Prior Probability)

P(B|A)/P(B)叫做似然度(Likelihood)

那么我们可以看出，贝叶斯定理可以比较简单的归纳为：

后验概率=先验概率*似然度

在日常使用中，如贝叶斯分类、贝叶斯回归、贝叶斯滤波等算法，普遍使用迭代和归一化的方法来计算似然度，为了更好的了解归一化的方法，这里还有一个基础概念，叫全概率公式。

接着之前的说法，很明显有

OK，先举几个经典的例子来帮助理解：

一座别墅在过去的 20 年里一共发生过 2 次被盗，别墅的主人有一条狗，狗平均每周晚上叫 3 次，假设在盗贼入侵时狗叫的概率被估计为 0.9，问题是：在狗叫的时候发生入侵的概率是多少？

我们假设：

事件A：狗在晚上叫

事件B：盗贼入侵

以天为单位统计,有：

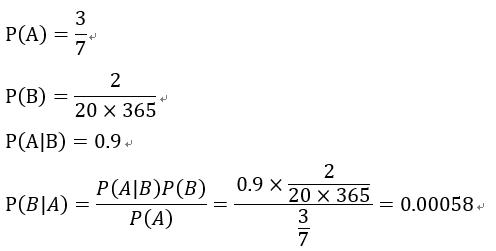
可以看到，最终的结果基本是不可能。

这只是一个最简单的例子，其中，别墅在过去的20年中被盗2次、狗平均每周晚上叫3次这些都是先验统计，而在现实应用中往往是根据上一步的事件去推断下一步的事件，这个迭代的过程往往是很多算法实现的基础。

下面，我们举一个更复杂一些的例子：

假设有两个各装了100个球的箱子，A箱子中有70个红球，30个蓝球，B箱子中有30个红球，70个蓝球。假设随机选择其中一个箱子，从中拿出一个球记下球色再放回原箱子，如此重复12次，记录得到8次红球，4次蓝球。问题来了，你认为被选择的箱子是A箱子的概率有多大？

我们假设得到小球的结果顺序如下：红红红红红红红红蓝蓝蓝蓝，用C++实现：

#include <iostream>
#include <cmath>
#include <iomanip>
#include <vector>
#include <cstdlib>
#include <ctime>
#include <limits>

class balls_case_problem
{
private:
  double p_a;
  double p_b;
  double p_red_in_a;
  double p_blue_in_a;
  double p_red_in_b;
  double p_blue_in_b;

public:
  balls_case_problem(int red_balls_in_a, int blue_balls_in_a, int red_balls_in_b, int blue_balls_in_b)
  {
    p_a = 0.5;
    p_b = 1 - p_a;

    p_red_in_a = (double)red_balls_in_a / (double)(red_balls_in_a + blue_balls_in_a);
    p_blue_in_a = 1 - p_red_in_a;

    p_red_in_b = (double)red_balls_in_b / (double)(red_balls_in_b + blue_balls_in_b);
    p_blue_in_b = 1 - p_red_in_b;
  }

  ~balls_case_problem(){};

  void got_red()
  {
    p_a = (p_red_in_a * p_a) / ((p_red_in_a * p_a) + (p_red_in_b * p_b));
    p_b = 1 - p_a;
  }

  void got_blue()
  {
    p_a = (p_blue_in_a * p_a) / ((p_blue_in_a * p_a) + (p_blue_in_b * p_b));
    p_b = 1 - p_a;
  }

  double get_p_a()
  {
    return p_a;
  }

  double get_p_b()
  {
    return p_b;
  }
};

int main()
{
  int red_ball_results[] = {1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0};
  balls_case_problem problem(70, 30, 30, 70);

  for(int i = 0; i < sizeof(red_ball_results) / sizeof(int); i++)
  {
    if(red_ball_results[i] == 1)
    {
      problem.got_red();
    }else{
      problem.got_blue();
    }
    std::cout << "Probility of chose case A: " << problem.get_p_a() << std::endl;
  }

  return 0;
}

运行结果为：

Probility of chose case A: 0.7
Probility of chose case A: 0.844828
Probility of chose case A: 0.927027
Probility of chose case A: 0.967365
Probility of chose case A: 0.985748
Probility of chose case A: 0.993842
Probility of chose case A: 0.997351
Probility of chose case A: 0.998863
Probility of chose case A: 0.997351
Probility of chose case A: 0.993842
Probility of chose case A: 0.985748
Probility of chose case A: 0.967365