[CSP-S模拟测试]:小Y的图（最小生成树+LCA）

题目传送门（内部题131）

---

输入格式

　　第一行三个整数$n$、$m$和$Q$。
　　接下来$m$行每行三个整数$x$、$y$、$z$（$1\leqslant x,y\leqslant n,1\leqslant z\leqslant 1,000,000$），表示有一条连接$x$和$y$长度为$z$的边。
　　接下来$Q$行每行两个整数$x$、$y$（$x\neq y$），表示一组询问。

---

输出格式

　　$Q$行每行一个整数，表示一组询问的答案。

---

样例

样例输入：

5 5 4
1 2 3
1 3 2
3 2 1
1 4 5
2 4 4
1 2
1 4
3 5
2 4

样例输出：

2
4
-1
4

---

数据范围与提示

　　对于前$30\%$的测试数据，满足$1\leqslant n,m,Q\leqslant 1,000$。
　　对于另外$30\%$的测试数据，保证图联通。
　　对于$100\%$的测试数据，满足$1\leqslant n,m,Q\leqslant 300,000$。
　　对于$100\%$的测试数据，保证不存在自环，但可能存在重边。
　　请使用$scanf,printf$或速度更快的读入输出方式。

---

题解

有人问我$30\%$的暴力怎么打（问题是$ta$还$A$了）……

那我就简单说一下。

最短路思想，用$Dijkstra$，将原本的$dis[v]=dis[u]+e[i].w$改成$dis[v]=\max(dis[u],e[i].w)$就好了。

千万不要想当然，比方说下面这份代码$\downarrow$

认真看一下，虽说时间复杂度是对的，但是如果如下面这张图$\downarrow$

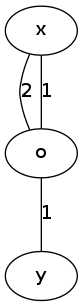
我们可能会选择$x\stackrel{2}{\rightarrow}o\stackrel{1}{\rightarrow}y$这条路径；然而当发现$x\stackrel{1}{\rightarrow}o$更优时会发现$o\rightarrow y$已经走过了，就不会再更新答案，这也就是为什么最短路不是这么求。

现在来说正解吧，先来考虑联通的情况。

这个最优路径上的所有边一定位于最小生成树上，所以可以求$x,y$到$lca$上的最长边即可。

不联通的情况也无非就是记录一下两个点在不在一个联通块内即可。

时间复杂度：$\Theta(m\log m+q\log n)$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
struct node{int x,y,z;bool d;}b[300001];
struct rec{int nxt,to,w;}e[600001];
int head[300001],cnt,tot;
int n,m,Q;
int f[300001],depth[300001],bel[300001],fa[300001][21],mi[300001][21];
bool cmp(node a,node b){return a.z<b.z;}
int find(int x){return x==f[x]?x:f[x]=find(f[x]);}
void add(int x,int y,int w)
{
	e[++cnt].nxt=head[x];
	e[cnt].to=y;
	e[cnt].w=w;
	head[x]=cnt;
}
void dfs(int x)
{
	bel[x]=tot;
	for(int i=head[x];i;i=e[i].nxt)
	{
		if(depth[e[i].to])continue;
		depth[e[i].to]=depth[x]+1;
		fa[e[i].to][0]=x;
		mi[e[i].to][0]=e[i].w;
		for(int j=1;j<=20;j++)
		{
			fa[e[i].to][j]=fa[fa[e[i].to][j-1]][j-1];
			mi[e[i].to][j]=max(mi[e[i].to][j-1],mi[fa[e[i].to][j-1]][j-1]);
		}
		dfs(e[i].to);
	}
}
int LCA(int x,int y)
{
	if(depth[x]>depth[y])swap(x,y);
	int res=0;
	for(int i=20;i>=0;i--)
		if(depth[fa[y][i]]>=depth[x])
		{
			res=max(res,mi[y][i]);
			y=fa[y][i];
		}
	if(x==y)return res;
	for(int i=20;i>=0;i--)
		if(fa[x][i]!=fa[y][i])
		{
			res=max(res,max(mi[x][i],mi[y][i]));
			x=fa[x][i];y=fa[y][i];
		}
	return max(res,max(mi[x][0],mi[y][0]));
}
int main()
{
	scanf("%d%d%d",&n,&m,&Q);
	for(int i=1;i<=n;i++)f[i]=i;
	for(int i=1;i<=m;i++)scanf("%d%d%d",&b[i].x,&b[i].y,&b[i].z);
	sort(b+1,b+m+1,cmp);
	for(int i=1;i<=m;i++)
	{
		int x=find(b[i].x);
		int y=find(b[i].y);
		if(x==y)continue;
		b[i].d=1;
		f[y]=x;
	}
	for(int i=1;i<=m;i++)
		if(b[i].d)
		{
			add(b[i].x,b[i].y,b[i].z);
			add(b[i].y,b[i].x,b[i].z);
		}
	for(int i=1;i<=n;i++)
		if(!depth[i])
		{
			tot++;
			depth[i]=1;
			dfs(i);
		}
	while(Q--)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		if(bel[x]!=bel[y])puts("-1");
		else printf("%d\n",LCA(x,y));
	}
	return 0;
}

---

rp++