TensorFlow(2)Softmax Regression

Softmax Regression

Chapter

• Basics

  1. generate random Tensors
  2. Three usual activation function in Neural Network
  3. Softmax funcion

• Softmax Regression

  1. Logistic Regression
  2. Softmax Regression
  3. Examples

Basics

• generate random Tensors
• Three usual activation function in Neural Network
• Softmax funcion

generate random Tensors

   Two generally type of random distribute:

• uniform
• normal

In TensorFlow, they come in tf.random_normal() and tf.random_uniform() funcion.

Example:

import tensorflow as tf

# 正态分布
# tf.random_normal(shape,mean=0.0,stddev=1.0,dtype=tf.float32,seed=None,name=None)
b = tf.random_normal([5, 5],seed = 1234)
# 平均分布
# tf.random_uniform(shape,minval=0.0,maxval=1.0,dtype=tf.flaot32,seed=None,name=None)
c = tf.random_uniform([5,5], seed=12)

with tf.Session() as sees:
    mat1, mat2 = sees.run([b,c])
    print(mat1)
    print(mat2)

output:

[[ 0.51340485 -0.25581399  0.65199131  1.39236379  0.37256798]
 [ 0.20336303  1.24701834 -0.98333126  0.50439858  0.98600131]
 [-1.70049322  1.51739979  0.06326418  1.07656693  0.03294745]
 [-2.32479048 -1.44697022  0.56703895  0.10577387 -0.90796399]
 [-1.05107033 -1.63305104  1.22501576  0.83072805  1.28771544]]
[[ 0.63615251  0.92409146  0.67627728  0.50212514  0.96114957]
 [ 0.88567221  0.04360652  0.29879451  0.46695721  0.05440903]
 [ 0.82479727  0.28480017  0.98824406  0.67999697  0.66409671]
 [ 0.75018144  0.31693625  0.51552784  0.75187266  0.44445455]
 [ 0.07454526  0.04856801  0.35572827  0.2670846   0.4779768 ]]

Three usual activation function in Neural Network

• logistic function: (sigmoid function)

\[f(x)=\frac{1}{1+e^{-x}}
\]

• tanh function

\[tanh(x)=\frac{sinh(x)}{cosh(x)}=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}
\]

• ReLU (Rectified Linear Unit) function

\[f(x) =
\begin{cases}
0, & \text{if x $\le$ 0} \\
x, & \text{if $x$ $\gt$ 0}
\end{cases}
\]

TensorFlow Code:

# 常用的神经网络的三种激活函数(sigmoid, tanh, ReLu)
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

g = tf.Graph()
with g.as_default() as g:
    x = tf.placeholder(dtype=tf.float64)
    y = tf.nn.sigmoid(x)     # sigmoid函数
    # y = tf.nn.tanh(x)      # tanh函数
    # y = tf.nn.relu(x)      # ReLU函数

with tf.Session(graph=g) as sess:
    # x的范围为-10到10，均匀地取1000个点
    x_value = np.linspace(-10, 10, 1000)
    x, y = sess.run([x,y], feed_dict={x: x_value})

# 绘制函数图像
plt.plot(x,y)

plt.title('logistic Function')
plt.xlabel('x')
plt.ylabel('y')

plt.show()

Softmax Function

  The softmax function is a generalization of the logistic function that "squashes" a K-dimensional vector of arbitrary real values to a K-dimensional vector of real values, where each entry is in the range (0, 1], and all the entries add up to 1.

  The function is :

  In TensorFlow, we can use tf.nn.softmax() function.

Python Code:

# -*- coding: utf-8 -*-
import tensorflow as tf

import numpy as np

A = np.array([1.0,2.0,3.0,4.0,5.0,6.0])
exp_A = np.exp(A)
softmax_A = exp_A/sum(exp_A)
print(softmax_A)

tf_a = tf.constant(A)

with tf.Session() as sess:
    print(sess.run(tf.nn.softmax(tf_a)))

output:

[ 0.00426978  0.01160646  0.03154963  0.08576079  0.23312201  0.63369132]
[ 0.00426978  0.01160646  0.03154963  0.08576079  0.23312201  0.63369132]

Softmax Regression

• Logistic Regression
• Softmax Regression
• Examples

Logistic Regression

  Think logistic regression in a neural-network way.

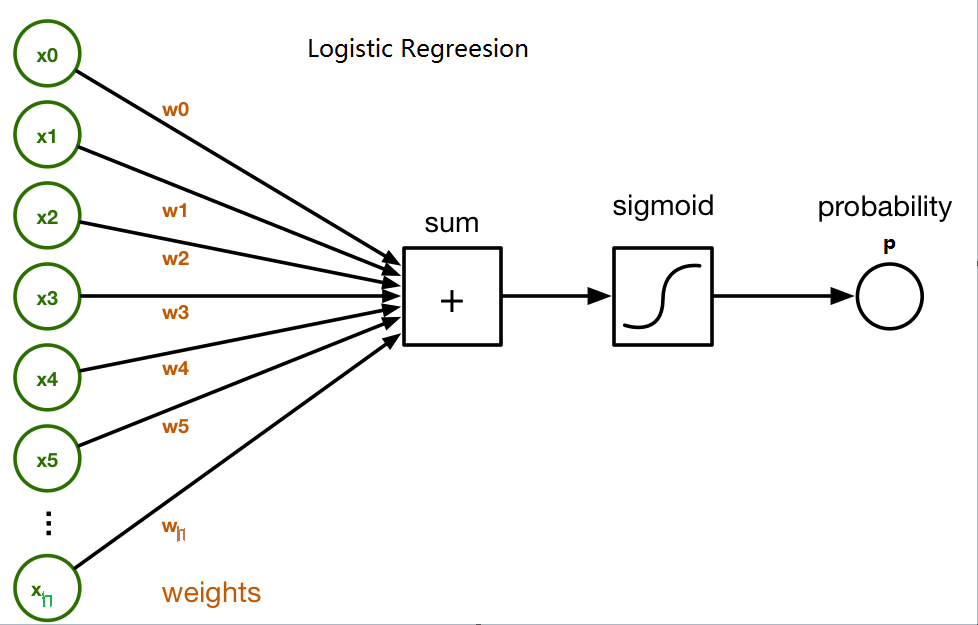
  Suppose there are m samples, each sample in n-dimension with label in {0,1}, so the loss function is:

\[\phi(x) = \sum\limits_{j=0}^{n}w_{j}x_{j}\\
h_{\theta}(x) =\frac{1}{1+e^{-\phi(x)}}
\]

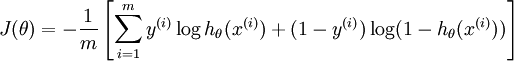
  We use gradient descent method to find the optimal parameter \(\theta\) (n+1 parameters: \(w_0,w_1,...,w_n\)) in order to minimize the loss.

Softmax Regression

  Softmax Regression is a generalize type of Logistic Function which is useful for multi-class classification.

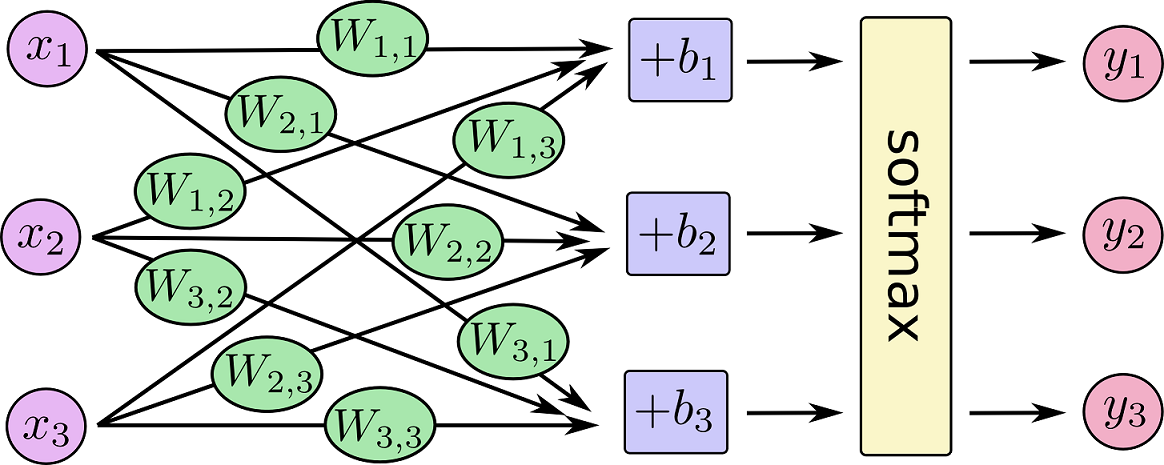
  Suppose there are m samples, each sample in n-dimension with label in {1,2,...,k}, so the loss function is:

\[J(\theta) = -\frac{1}{m}\Big[\sum\limits_{i=1}^{m}\sum\limits_{j=1}^{k}1{\{y^{(i)}=j\}}\times \log{(p(y^{(i)}=j|x^{i};\theta))}\Big]
\]

  We use gradient descent method to find the optimal parameter \(\theta\) (\(k\times (n+1)\) parameters) in order to minimize the loss.

TensorFlow Code:

import tensorflow as tf
import numpy as np
import logging

logging.basicConfig(level = logging.INFO, format='%(asctime)s - %(levelname)s: %(message)s')
logger = logging.getLogger(__name__)

class Softmax:

    def __init__(self, input_size, class_num, epoch = 1000, learning_rate = 0.1, save_model_path='./model.ckpt'):

        self.save_model_path = save_model_path   # 模型保存目录
        self.epoch = epoch                       # 循环次数
        self.learning_rate = learning_rate       # 学习率

        x = tf.placeholder(dtype=tf.float32, shape=[None, input_size])         # 特征
        y_true = tf.placeholder(dtype=tf.float32, shape=[None, class_num])     # 标签

        # 定义softmax回归的网络结构
        W = tf.Variable(tf.random_normal([input_size, class_num]), name='weight')
        b = tf.Variable(tf.random_normal([class_num]), name='bias')

        # tf.nn.softmax computes softmax activations
        # softmax = exp(logits) / reduce_sum(exp(logits), dim)
        self.hypothesis = tf.nn.softmax(tf.matmul(x, W) + b)

        self.x = x
        self.y_true = y_true

        # Cross entropy loss
        self.loss = tf.reduce_mean(-tf.reduce_sum(self.y_true * tf.log(self.hypothesis), axis=1))

        # 选择optimizer使loss达到最小, 使用梯度下降法减少 loss，学习率是self.learning_rate
        self.train_model = tf.train.GradientDescentOptimizer(self.learning_rate).minimize(self.loss)

        self.saver = tf.train.Saver()

        logger.info('Initialize the model...')

    # 训练并保存模型
    def train(self, x_data, y_data):

        logger.info('Training the model...')
        with tf.Session() as sess:

            # 对所有变量进行初始化
            sess.run(tf.global_variables_initializer())

            feed_dict = {self.x: x_data, self.y_true: y_data}
            # 进行迭代学习
            for i in range(self.epoch+1):
                sess.run(self.train_model, feed_dict=feed_dict)
                if i % int(self.epoch/10) == 0:
                    # to see the step improvement
                    print('已训练%d次, loss: %s.' % (i, sess.run(self.loss, feed_dict=feed_dict)))

            # 保存ANN模型
            logger.info('Saving the model...')
            self.saver.save(sess, self.save_model_path)  # E

    # 预测数据
    def predict(self, data):

        with tf.Session() as sess:
            logger.info('Restoring the model...')
            self.saver.restore(sess, self.save_model_path) # A
            predict = sess.run(self.hypothesis, feed_dict={self.x: data}) # B
            predict_class = sess.run(tf.argmax(predict,1))

        print("预测值为：%s." % predict_class)

        return predict

# 使用Softmax类
# 样本数据

x_data = np.array([[1, 2, 1, 1],
                   [2, 1, 3, 2],
                   [3, 1, 3, 4],
                   [4, 1, 5, 5],
                   [1, 7, 5, 5],
                   [1, 2, 5, 6],
                   [1, 6, 6, 6],
                   [1, 7, 7, 7]])

y_data = np.array([[0, 0, 1],
                   [0, 0, 1],
                   [0, 0, 1],
                   [0, 1, 0],
                   [0, 1, 0],
                   [0, 1, 0],
                   [1, 0, 0],
                   [1, 0, 0]])

input_size = x_data.shape[1]
class_num = y_data.shape[1]

save_path = 'E://logs/model.ckpt'
st = Softmax(input_size, class_num, 1000, 0.1, save_path)
st.train(x_data, y_data)
st.predict(np.array([[1, 3, 4, 3]]))

output:

2018-08-17 17:01:37,854 - INFO: Initialize the model...
2018-08-17 17:01:37,854 - INFO: Training the model...
已训练0次, loss: 5.31073.
已训练100次, loss: 0.624064.
已训练200次, loss: 0.559649.
已训练300次, loss: 0.511522.
已训练400次, loss: 0.470231.
已训练500次, loss: 0.432752.
已训练600次, loss: 0.397538.
已训练700次, loss: 0.363444.
已训练800次, loss: 0.329436.
已训练900次, loss: 0.294607.
已训练1000次, loss: 0.259079.
2018-08-17 17:01:38,289 - INFO: Saving the model...
2018-08-17 17:01:39,062 - INFO: Restoring the model...
INFO:tensorflow:Restoring parameters from E://logs/model.ckpt
2018-08-17 17:01:39,062 - INFO: Restoring parameters from E://logs/model.ckpt
预测值为：[0].

Examples

iris.csv: https://github.com/percent4/Storing_pictures/blob/master/iris.csv

TensorFlow Code:

Softmax 类：TF_Softmax.py

import tensorflow as tf
import logging

logging.basicConfig(level = logging.INFO, format='%(asctime)s - %(levelname)s: %(message)s')
logger = logging.getLogger(__name__)

class Softmax:

    def __init__(self, input_size, class_num, epoch = 1000, learning_rate = 0.1, save_model_path='./model.ckpt'):

        self.save_model_path = save_model_path   # 模型保存目录
        self.epoch = epoch                       # 循环次数
        self.learning_rate = learning_rate       # 学习率

        x = tf.placeholder(dtype=tf.float32, shape=[None, input_size])         # 特征
        y_true = tf.placeholder(dtype=tf.float32, shape=[None, class_num])     # 标签

        # 定义softmax回归的网络结构
        W = tf.Variable(tf.random_normal([input_size, class_num],  name='weight'))
        b = tf.Variable(tf.random_normal([class_num],  name='bias'))

        # tf.nn.softmax computes softmax activations
        # softmax = exp(logits) / reduce_sum(exp(logits), dim)
        self.hypothesis = tf.nn.softmax(tf.matmul(x, W) + b)

        self.x = x
        self.y_true = y_true

        # Cross entropy loss
        self.loss = tf.reduce_mean(-tf.reduce_sum(self.y_true * tf.log(self.hypothesis), axis=1))

        # 选择optimizer使loss达到最小, 使用梯度下降法减少 loss，学习率是self.learning_rate
        self.train_model = tf.train.GradientDescentOptimizer(self.learning_rate).minimize(self.loss)

        self.saver = tf.train.Saver()

        logger.info('Initialize the model...')

    # 训练并保存模型
    def train(self, x_data, y_data):

        logger.info('Training the model...')
        with tf.Session() as sess:

            # 对所有变量进行初始化
            sess.run(tf.global_variables_initializer())

            feed_dict = {self.x: x_data, self.y_true: y_data}
            # 进行迭代学习
            for i in range(self.epoch+1):
                sess.run(self.train_model, feed_dict=feed_dict)
                if i % int(self.epoch/10) == 0:
                    # to see the step improvement
                    print('已训练%d次, loss: %s.' % (i, sess.run(self.loss, feed_dict=feed_dict)))

            # 保存ANN模型
            logger.info('Saving the model...')
            self.saver.save(sess, self.save_model_path)  # E

    # 预测数据
    def predict(self, data):

        with tf.Session() as sess:
            logger.info('Restoring the model...')
            self.saver.restore(sess, self.save_model_path) # A
            predict = sess.run(self.hypothesis, feed_dict={self.x: data}) # B

        # print("预测值为：%s." % predict)

        return predict

预测数据：test_softmax.py

"""
利用Softmax对IRIS数据集进行多分类
"""

from TF_Softmax import Softmax
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.preprocessing import LabelBinarizer

CSV_FILE_PATH = 'E://iris.csv'          # CSV 文件路径
IRIS = pd.read_csv(CSV_FILE_PATH)       # 读取CSV文件

target_variable = 'class'               # 目标变量

# 数据集的特征
features = list(IRIS.columns)
features.remove(target_variable)

# 目标变量的类别
Class = IRIS[target_variable].unique()

# 对目标变量进行重新编码

# 目标变量的类别字典
Class_dict = {}
for i, clf in enumerate(Class):
    Class_dict[clf] = i+1
# 增加一列target, 将目标变量进行编码
IRIS['target'] =  IRIS[target_variable].apply(lambda x: Class_dict[x])

# 对目标变量进行0-1编码
lb = LabelBinarizer()
lb.fit(list(Class_dict.values()))
transformed_labels = lb.transform(IRIS['target'])
y_bin_labels = []   # 对多分类进行0-1编码的变量
for i in range(transformed_labels.shape[1]):
    y_bin_labels.append('y'+str(i))
    IRIS['y'+str(i)] = transformed_labels[:, i]
# print(IRIS.head(100))

# 数据是否标准化
# x_bar = (x-mean)/std
IS_STANDARD = 'no'
if IS_STANDARD == 'yes':
    for feature in features:
        mean = IRIS[feature].mean()
        std = IRIS[feature].std()
        IRIS[feature] = (IRIS[feature]-mean)/std

# print(IRIS.head())

# 将数据集分为训练集和测试集，训练集80%, 测试集20%
x_train, x_test, y_train, y_test = train_test_split(IRIS[features], IRIS[y_bin_labels], \
                                                    train_size = 0.8, test_size=0.2, random_state=123)

# 使用Softmax进行预测
# 构建Softmax网络
input_size = x_train.shape[1]
class_num = y_train.shape[1]

# 模型保存地址
MODEL_SAVE_PATH = 'E://logs/softmax.ckpt'
# Softmax初始化
ann = Softmax(input_size, class_num, 10000, 0.5, MODEL_SAVE_PATH)
ann.train(x_train, y_train)            # 训练ANN
y_pred = ann.predict(x_test)     # 预测数据

# 预测分类
prediction = []
for pred in y_pred:
    prediction.append(list(pred).index(max(pred))+1)

# 计算预测的准确率
x_test['prediction'] = prediction
x_test['label'] = IRIS['target'][y_test.index]
print(x_test.head())
accuracy = accuracy_score(x_test['prediction'], x_test['label'])
print('Softmax预测准确率为%.2f%%.'%(accuracy*100))

output:

2018-08-17 21:36:33,373 - INFO: Initialize the model...
2018-08-17 21:36:33,373 - INFO: Training the model...
已训练0次, loss: 8.691852.
已训练1000次, loss: 0.060822684.
已训练2000次, loss: 0.053384975.
已训练3000次, loss: 0.04848685.
已训练4000次, loss: 0.044897027.
已训练5000次, loss: 0.042198572.
已训练6000次, loss: 0.040111676.
已训练7000次, loss: 0.038444195.
已训练8000次, loss: 0.037071057.
已训练9000次, loss: 0.035911743.
已训练10000次, loss: 0.034913346.
2018-08-17 21:36:37,012 - INFO: Saving the model...
2018-08-17 21:36:37,215 - INFO: Restoring the model...
INFO:tensorflow:Restoring parameters from E://logs/softmax.ckpt
2018-08-17 21:36:37,230 - INFO: Restoring parameters from E://logs/softmax.ckpt
     sepal_length  sepal_width  petal_length  petal_width  prediction  label
72            6.3          2.5           4.9          1.5           2      2
112           6.8          3.0           5.5          2.1           3      3
132           6.4          2.8           5.6          2.2           3      3
88            5.6          3.0           4.1          1.3           2      2
37            4.9          3.1           1.5          0.1           1      1
Softmax预测准确率为96.67%.